在学习机器学习相关算法原理和推导（比如线性回归和Logistic回归）的时候，经常会遇到矩阵微分运算，一个步骤看不懂，很影响之后的推导。找的教程发现，有的教程有深度，但缺乏条理，阅读体验很差；维基百科全面，但过于冗长，检索所需知识比较慢，学习成本过高。因此，有了本文。

文章目录

1. 线性拟合
2. 矩阵求导

2.1 对标量求导（Derivatives by Scalar）

2.1.1 向量对标量求导
2.1.2 矩阵对标量求导

2.2 对向量求导（Derivatives by Vector）

2.2.1 标量对向量求偏导
2.2.2 向量对向量求偏导

2.3 矩阵导数（Derivative by Matrix）

2.3.1 标量对矩阵求导

2.4 注意事项
2.5 常用求导公式

3. 常用求偏导公式

3.1 数学符号说明
3.2 标量对标量求导（Derivatives of Scalar by Scalar）
3.3 向量对标量求导（Derivatives of Vector by Scalar）
3.4 矩阵对标量求导（Derivatives of Matrix by Scalar）
3.5 标量对向量求导（Derivatives of Scalar by Vector）
3.6 矩阵对标量求导（Derivatives of Scalar by Matrix）
3.7 向量对向量求导（Derivatives of Vector by Vector）

4. 分母布局注意事项
5. 混合求导公式

5.1 常用公式
5.2 使用矩阵微分证明伪逆最小化和平方误差

1. 线性拟合

线性拟合问题建模流程：

给定含有 $n$ 个样本的数据集 $p_i = [x_{i1} \cdot \cdot \cdot x_{im}]^T , 1\le i \le n$ ，及其对应的输出值 $v_i$ ；
找到一个线性函数 $f$ 使得预测输出与期望输出之差的平方和 $E$ 最小；

$E = \sum^{n}_{i=1} (f(p_i) − v_i)^2 \tag{1}$

线性函数 $f(p_i)$ 有如下形式：
$f(p) = f(x_1, . . . , x_m) = a_1x_1+ · · · + a_mx_m+ a_{m+1} \tag{2}$
将数据集记为矩阵方程式的形式：
$D \ a = v \tag{3}$

上式中， $D$ 为样本数据， $a$ 权重矩阵， $v$ 为样本标签；各变量的维度为：
在这里插入图片描述
因此由等式 (3) 可以计算得：
$a = (D^TD)^{−1}D^Tv \tag{5}$

说明： $p_i = [x_{i1} \cdot \cdot \cdot x_{im}]^T, 1\le i \le n$ 表示一个有 $n$ 个样本的数据集，每个样本有 $m$ 个特征。因此易知：

矩阵 $D$ 的shape为 $n \times (d+1)$ ；
矩阵 $D^T$ 的shape为 $(d+1) \times n$ ；
矩阵 $D^TD$ 的shape为 $n \times n$ 的满秩方阵，所以 $D^TD$ 是可逆的。

由此容易证明公式(5)成立，证明过程：等式(3)两边同时左乘 $D^T$ ，然后同时左乘 $(D^TD)^{-1}$ ，得到公式(5)，证毕。

将 $D$ 的每一行表示为 $d^T_i$ 有：
$E = \sum^n_{i=1}(d^T_ia − v_i)^2 = ||D \ a − v||^2 \tag{6}$

注意： $d_i$ 表示一个样本，该样本有 $m$ 个特征，shape为 $m \times 1$ ；因此 $d^T_i$ 的shape为 $1 \times m$ ；

因此，线性最小二乘问题可以简化为：
$min_a = ||D \ a − v||^2 \tag{7}$

现在我们需要最小化误差 $E$ ，由等式(5)和(6)得：
$\frac{dE}{da}=0 \tag{8}$

公式(8)应该如何求解？
显示计算（头发掉干净运算、枯燥运算、不漂亮运算）：
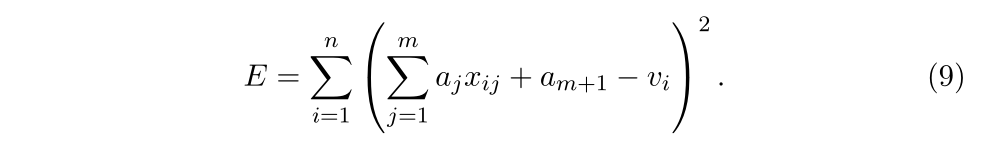
在这里插入图片描述
展开方程计算：

然后令 ${\partial E}/{\partial a_k}= 0$ 计算 $a_k$ 。

这种方式计算太慢并且容易出错。那该咋算？接下来引入矩阵求导（Matrix Derivatives）。

2. 矩阵求导

矩阵导数有6种常见类型：

小写默认字体表示标量（Scalar），小写加粗字体表示向量（Vector），大写加粗字体表示矩阵（Matrix） 。下面分别介绍。

2.1 对标量求导（Derivatives by Scalar）

2.1.1 向量对标量求导

在这里插入图片描述

2.1.2 矩阵对标量求导

在这里插入图片描述

2.2 对向量求导（Derivatives by Vector）

2.2.1 标量对向量求偏导

在这里插入图片描述

2.2.2 向量对向量求偏导

在这里插入图片描述
左边为分子布局形式，右边为分母布局形式。

2.3 矩阵导数（Derivative by Matrix）

2.3.1 标量对矩阵求导

在这里插入图片描述

辅助记忆：
在这里插入图片描述

2.4 注意事项

采用分子布局还是分母布局这两种形式，大多数书籍和论文都没有说明使用哪种。最好不要在公式中混用这两种形式。本文内容采用分子布局表示法。

2.5 常用求导公式

下文公式中的符号规定：

小写不加粗字体的a为标量；
小写加粗字体的a为向量；
大写加粗字体表示矩阵A；
矩阵A不是标量x和向量x的函数。

在这里插入图片描述

3. 常用求偏导公式

3.1 数学符号说明

规定向量 $X$ 表示为列矩阵， $X^T$ 为行矩阵。

$X=\left[ \begin {array}{c} x_1\\ x_2\\ \vdots\\ x_m\\ \end {array}\right ]$

$X^T = [x_1 \ x_2 \ · · · \ x_m]$

考虑两个有相同纬度的列向量 $x$ 和 $y$ ，它们的内积 $x^Ty$ 实际上是1×1矩阵：
$x^Ty = [s]$
其中
$s= \sum^m_{i=1} x_iy_i$
为了表示上的不便，我们通常去掉矩阵，把内积看作标量，即
$x^Ty= \sum^m_{i=1} x_iy_i$