3 容斥原理与鸽巢原理

3.1 De Morgan定理

3.2容斥定理

3.3容斥原理举例

3.4棋盘多项式与有限制条件的排列

3.10 n对夫妻问题

• n对夫妻圆桌
  • 夫妻不相邻方案数

 

• (1)n对夫妻围圆桌夫妻相邻方案数
  $(n-1)!2^n$
• $A_i$:第 $i$对夫妻相邻的集合
• 所问问题为求

 

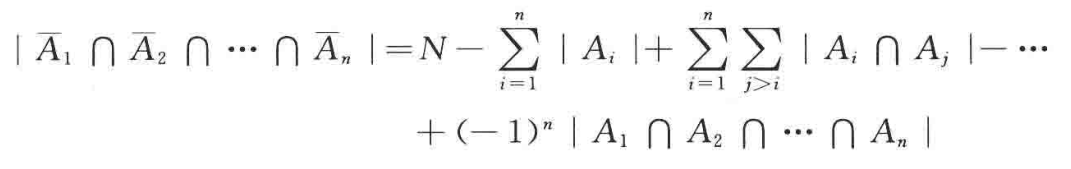
• (2)

• $2n$个人圆桌方案数 $(2n-1)!$

• $A_i$相当于将第 $i$对夫妻作为一个对象围圆桌而坐然后换位,

• 故
  $A_i=2(2n-2)!$

• 故夫妻不相邻的方案数

3.15 Ramsey数

3.15.1 Ramsey 问题

• 例3-37
• 6人,至少3个人或互相认识,或互不相识
• A,B,C,D,E,F,过此6个顶点作完全图,见图3-13,
• 互相认识的两人,连红色
• 不相认识的两个人着蓝色

 

• 等价于证明6个点的完全图,用红蓝二色任意着色,
• 至少存在一个红色三角形,或蓝边三角形

 

• A和其他5个点相连5条边,每条边或红,或蓝
  • 至少 $\lfloor \frac{5-1}{2}\rfloor+1=3$边同色
• 不妨假定3条红色
  • 3条边的另外3端点L,M,N.
  • 这3个端点间的连线或同色或不同色.
• 若是前者,则已存在一个同色三角形,
  • 或是红色或是蓝色,均满足 Ramsey问题的结论,
• 若是后者,依据鸽巢原理,至少有一条边是红色,
  • 设为(L,M),则ALM构成一个红色边三角形.