SVM中的对偶问题以及KKT条件

一、拉格朗日求解最优化问题

我们这里提到的最优化问题通常是指对于给定的某一函数，求其在指定作用域上的全局最小值。在求解最小值时一般有三种情况：无约束、等值约束和不等式约束。五约束条件直接求导即可。等式约束要用到拉格朗日求解。当遇到不等式约束问题便要加上我们下面会谈到的KKT条件。首先说一下等式约束求解最优解问题。

先解释为什么拉格朗日的方法可以求解带有等值约束的函数最优化问题：

min f(x,y)

s.t. g(x,y) = c

这里画出z=f(x,y)的等高线：

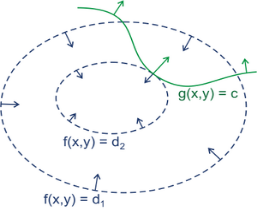
其中绿线标出的是约束的点的轨迹。蓝线是的等高线。箭头表示斜率，斜率和等高线的法线平行。从梯度的方向上来看，如果没有这条约束，的最小值应该会落在最小那圈等高线内部的某一点上（梯度向内，盆地型）。而现在加上了约束，最小值点应该在哪里呢？显然应该是在的等高线正好和约束线相切的位置，因为如果只是相交意味着肯定还存在其它的等高线在该条等高线的内部或者外部，使得新的等高线与目标函数的交点的值更大或者更小，只有到等高线与目标函数的曲线相切的时候，可能取得最优值。

如果我们对约束也求梯度，则其梯度如图中绿色箭头所示。很容易看出来，要想让目标函数的等高线和约束相切，则他们切点的梯度一定在一条直线上。

即：∇f(x,y)=λ（∇g(x,y)-C)

其中λ可以是任何非0实数。一旦求出λ的值，将其套入下式，易求在无约束极值和极值所对应的点。

这就是拉格朗日函数的由来。

二、KKT条件

下面再说不等式约束条件：

设目标函数f(x)，不等式约束为g(x)，有时还会有还会有等式约束条件h(x)。此时的约束优化问题描述如下：

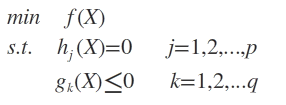
则我们定义不等式约束下的拉格朗日函数L，则L表达式为：

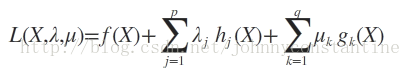
其中f(x)是原目标函数，hj(x)是第j个等式约束条件，λj是对应的约束系数，gk是不等式约束，uk是对应的约束系数。

此时若要求解上述优化问题，必须满足下述条件（也是我们的求解条件）：

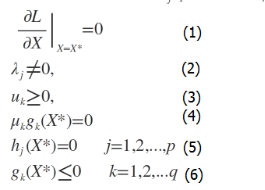
这些求解条件就是KKT条件。下面对KKT条件做出解释。

首先当约束条件变为不等式时，可行域由线变成了区域，如下图所示：

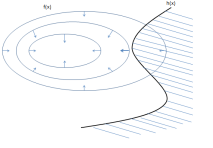
那么能取到极值点的地方可能有两种情况：

还是在h(x)和等值线相切的地方
f(x) 的极值点本身就在可行域里面。

因为如果不是相切，那么同样的，对任意一个在可行域中的点，如果在它附近往里走或者往外走，f(x)f(x)一般都会变大或者变小，所以绝大部分点都不会是极值点。除非这个点刚好在交界处，且和等值线相切；或者这个点在可行域内部，但是本身就是 f(x)的极值点。如下图：

对于相切的情况（右图所示情况）不等式约束就变成等式约束了，所以此时g(x)=0。对于另一种情况（如左图所示），约束g(x)<=0不起任何作用，它等价于对 f(x)+λh(x)用拉格朗日乘子法（也就是说可以将其直接去掉）。

把两种情况用一个式子表示出来即得到KKT中的条件（4），也就是μg(x)=0。

这里需要再解释一下条件三，即u>=0。当出现上图中左图情况，我们让u=0，使之转化为求解f(x)+λh(x)问题。当出现右图所示状况时，就转化成了等式约束问题，那么就回到了要让 ∇f(x,y)+u(∇g(x,y))=0 的问题。我们已经知道了问题中的可行域是在 g(x)≤0一侧，而 g(x)的梯度是指向大于 0 的一侧，也就是不是可行域的一侧。而求的问题是极小值，所以 f(x)在交点处的梯度是指向可行域的一侧，也就是说两个梯度一定是相反的。所以u要大于零。所以u>=0。

而上面我们说到的等式约束情况，由于不知道 h(x)的梯度方向，所以对它没有约束，对λ没有这个约束。

三、SVM中的对偶问题

（1）对偶问题

首先原始问题是：

则我们定义不等式约束下的拉格朗日函数L，则L表达式为：

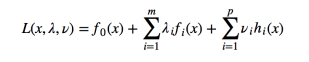
现在我们设如下函数：

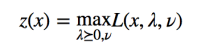
因为满足约束条件的 x 会使得 hi(x)=0 ，因此最后一项消掉了，而 fi(x)≤0 ，并且我们要求了 λ⪰0 ，因此 λifi(x)≤0 ，所以最大值只能在它们都取零的时候得到，这个时候就只剩下 f0(x) 了。因此，对于满足约束条件的那些 x 来说，f0(x)=z(x) 。这样一来，原始的带约束的优化问题其实等价于如下的无约束优化问题：

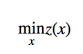
也就是，

然后我们将min和max对调即可得到关于原始问题的对偶问题。现在我们设函数：

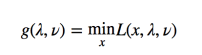
上面这个性质叫做弱对偶性，对于所有的优化问题都成立。既然有弱对偶性，那必然有强对偶性，前对偶性指的原始问题和对偶问题的最优解严格相等，即：

在强对偶性成立的情况下，我们就可以通过对原始问题的对偶问题的求解来得到最优解（SVM就是这么做的），但并不是所有情况下强对偶性都成立，它会有一定的前提。

（2）Slater 条件

首先我们介绍一下Slater 条件，Slater 条件是指存在严格满足约束条件的点 x ，这里的“严格”是指 fi(x)≤0 中的“小于或等于号”要严格取到“小于号”，亦即，存在 x 满足：

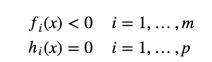
我们有：如果原始问题是凸优化问题（SVM的规划问题是一个凸优化问题）的并且满足 Slater 条件的话，那么 strong duality 成立。需要注意的是，这里只是指出了 strong duality 成立的一种情况，而并不是唯一情况，不过研究SVM的话，知道这种情况足够了。所以SVM是属于强对偶情况，故我们可以将原问题转化为对偶问题求解。

（3）再谈KKT

让我们回到 duality 的话题。来看看 strong duality 成立的时候的一些性质。假设 x∗ 和 (λ∗,ν∗) 分别是 primal problem 和 dual problem 的极值点，相应的极值为 p∗ 和 d∗ ，首先 p∗=d∗ ，此时我们可以得到：