SVM的拟合过程
1、怎么做
二分类的思路，简单说就是确定一条直线,也就是确定参数w和b。参数w和b知道后，再给一个样本x,带入到上面的公式，如果y≥+1，就判断为正类（+1），如果y≤-1，就判断为负类（-1）。这条直线或超平面怎么找呢？假设标签为{+1，-1}。要想更好的分开这两类数据，在数据上划出两条线，使这两类数据之间的间隔最大，对应图中的虚线。在两条虚线的中间画一条直线，对应图中橙色的线，就是我们需要找的分割线。
我们要做的就是最大化两条虚线之间的距离，这两条虚线的距离=d*2 ，其中，在SVM中两条直线的距离公式为：
。所以，我们要最大化这个式子，也就等于最小化||W||， 等价于最小化||W||^2,即：
另一方面，我们要最小化这个式子，这个式子的表达是有限制条件的，即：
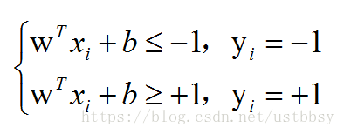
如此一来我们便得到了SVM的数学模型：（后面解出该模型即可得到SVM）
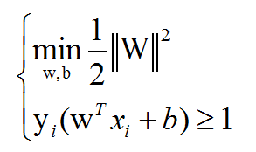
2、关于SVM数学模型的求解
首先我们先说几个概念：
拉格朗日乘子法：是一种寻找多元函数在一组约束下的极值的方法。通过引入拉格朗日乘子，可将d个变量与k个约束条件的最优化问题转化为具有d+k个变量的无约束优化问题求解 对于SVM基本型，我们要用到拉格朗体乘数法进行求解，由于约束条件中还带有不等式约束，所以还需要考虑KKT条件。
通常的优化问题有三种：
- 无约束优化问题
- 约束条件有等式优化问题
- 约束条件有不等式优化问题
分别考虑这几种情况：（1）无约束优化问题：求导，令导数为0，求得的解就是极值，随后从中选出最优解。2）约束条件有等式优化问题：使用拉格朗日乘数法，把等式约束 乘以一个拉格朗日系数并与 加在一个式子中，这个函数称为拉格朗日函数，而系数称为拉格朗日乘子。通过拉格朗日函数对各个变量求导，令其为零，可以求得候选值集合，然后验证求得最优值。（3）约束条件有不等式优化问题：同样使用拉格朗体乘数法，最常使用的就是KKT条件。与前面一样，将所有等式约束与不等式约束和写为一个函数，拉格朗日函数。通过一些条件，这些条件是可以求出最优值的必要条件，这个条件就是KKT条件。
现在我们将前面讲到的数学模型转化为拉格朗日形式：
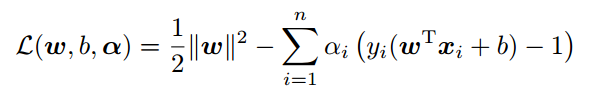
对W,b求导，令其分别为0，可得：
将其回代，可以得到原数学模型的关于 α的对偶问题：
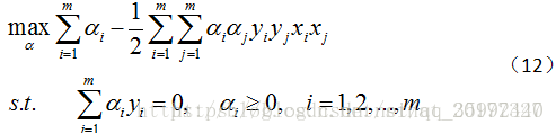
解出 α 之后，可以求得 w ， 进而求得 b，便可到模型。（其中 α 的求解是一个二次规划过程，会涉及到SMO）
3、SVM中的线性不可分情况（软间隔）
3.1 简述
如图一，就是一个典型的线性不可分的分类图，我们没有办法用一条直线去将其分成两个区域，每个区域只包含一种颜色的点。要想在这种情况下的分类器，有两种方式，一种是用曲线去将其完全分开（图一），曲线就是一种非线性的情况，跟之后将谈到的核函数有一定的关系。
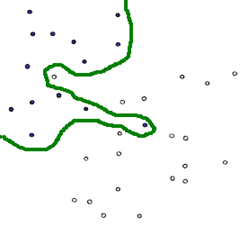
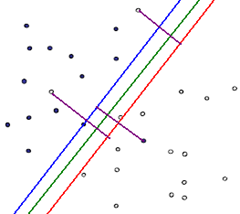
图一 图二
另外一种还是用直线（图二），不过不用去保证可分性，就是包容那些分错的情况，不过我们得加入惩罚函数，使得点分错的情况越合理越好。其实在很多时候，不是在训练的时候分类函数越完美越好，因为训练函数中有些数据本来就是噪声，可能就是在人工加上分类标签的时候加错了，如果我们在训练（学习）的时候把这些错误的点学习到了，那么模型在下次碰到这些错误情况的时候就难免出错了。这种学习的时候学到了“噪声”的过程就是一个过拟合（over-fitting）。我们可以为分错的点加上一点惩罚，对一个分错的点的惩罚函数就是这个点到其正确位置的距离。所以直观来说就是，软间隔允许分类出现错误。
3.2 软间隔中的惩罚因子和松弛变量：
关于惩罚因子，在上述内容中我们提到对错分点的惩罚函数（这个点到其正确位置的距离），在这里可以引入惩罚因子“C”，用C来控制学习器对错分样本点的重视程度。
下面再说一下松弛变量。有时我们找的直线，它们中间有一些散落的点，这些点不满足SVM的限制条件。如下图所示：
对于这种情况，我们就可以引入松弛变量ξ（ξ≥0）。
如下面图一所示，ξ即为我们引入的松弛变量，可以看出，这样一来红点和分割线的函数距离就可以表示为 
，如此一来所有样本点就都满足了限制条件。此时SVM的数学模型就变为图二所示内容。（注意图二公式中的松弛变量ξ，在此处作为惩罚值（可以将ξ理解为距离的变形），而C为惩罚因子，并不是所有样本点都有松弛变量，只有离群点才有）
（图一） （图二）
（注：此例比较有局限性，松弛变量不仅仅可以针对在-1~1之间的样本点，对于所有错分样本点皆可适用）
好，以上我们说完了SVM的拟合问题，后面会说一下SVM中的核函数和SMO。
