【Electromagnetic Field and Electromagnetic Wave】2 —— 透彻理解梯度、散度与旋度

一、标量场的梯度

1.1 从等值面与方向导数说起

方向导数（标量） 的计算：比如说我们给出了一个标量场函数： $u(x, y, z)$，下面要计算这个标量场内一点 $M_0$ 处的方向导数，计算公式是这样的： $\frac{\partial{u}}{\partial{l}} = \frac{\partial{u}}{\partial{x}}cosα + \frac{\partial{u}}{\partial{y}}cosβ + \frac{\partial{u}}{\partial{z}}cosγ$
方向导数反应的是在标量场里面，从 $M$ 点开始沿着某一方向 $\overrightarrow{l}$ 距离的变化率。

那么，如果我们知道了方向 $\overrightarrow{l}$，是需要会计算方向余弦的。计算方法是：比如我们要计算 $cosα$，（也即是 $x$ 方向的方向余弦）那么我们就用向量 $(1, 0, 0)$ 去我们的方向向量 $\overrightarrow{l}$ 做点乘运算，就可以把 $cosα$ 求出来。

1.2 梯度的意义与计算

梯度，他是一个矢量。它的计算公式如下： $\overrightarrow{grad \space u} = \frac{\partial{u}}{\partial{x}}\overrightarrow{a_x} + \frac{\partial{u}}{\partial{y}}\overrightarrow{a_y} + \frac{\partial{u}}{\partial{z}}\overrightarrow{a_z}$

如果当 $\overrightarrow{l}$ 和梯度的方向一致，那么就表示是场函数 $u(x,y,z)$ 变化最快的方向，最大变化率就是梯度的模值： $|\overrightarrow{grad \space u} | = \sqrt{\frac{\partial{u}}{\partial{x}}^2+\frac{\partial{u}}{\partial{y}}^2+\frac{\partial{u}}{\partial{z}}^2}$

而标量场沿着任意方向的方向导数就等于梯度在这个方向上的投影！，表示为： $\frac{\partial{u}}{\partial{l}} = \overrightarrow{gradu} \sdot \overrightarrow{a_l}$

二、矢量场的散度

2.1 从通量说起

首先，什么是通量呢？—— 简单点说，就是单位时间内通过某一面积的曲面的量。

我们以下面这个不封闭的曲面为例：我们可以将这个大曲面（设面积为 $S$）分割成若干个子区域对吧，每一个子区域的面积是 $dS$， $dS$ 曲面的单位法向矢量是 $\overrightarrow{a_n}$。这里还需要说明一件事情：

对于不封闭的曲面来说，其单位法向矢量与曲面构成右手螺旋定则。因此，下图中的 $\overrightarrow{a_n}$ 方向向上

通过 $dS$ 面的量，我们可以用 $\overrightarrow{A}$ • $\overrightarrow{a_n}$表示，那么根据积分的定义，通过整个面积为 $S$ 的曲面的量就可以表示成 $Φ=\iint_S\overrightarrow{A}\sdot \overrightarrow{a_n} \space dS\tag{1}$
其中， $\overrightarrow{A}$ • $\overrightarrow{a_n}$表示矢量 $\overrightarrow{A}$ 在 $\overrightarrow{a_n}$方向上的投影。那么，类似地，如果这个曲面是面积为 $S$ 的闭合曲面，那么有 $Φ = \oiint_S\overrightarrow{A}\sdot \overrightarrow{a_n} \space dS\tag{2}$
式（1）、（2）就是我们所说的通量了！注意：从上式的形式可以看出：通量是个标量！

2.2 散度及其推导

下面我们就想啊：假如是闭合曲面，讲道理净通量 $Φ$ 应该是 0，也就是说进入闭合曲面的矢量线有几条，那么穿出去的应该也是多少条。但是，常常会有下面的情况：

1. 如果 $Φ >0$ ，说明这个闭合曲面内部还有一个“发射”的东西（我们称之为能量正源），使得穿出曲面的矢量线条数增加了。
2. 如果 $Φ >0$ ，说明这个闭合曲面内部还有一个“吸收”的东西（我们称之为能量负源），它会吸收穿入曲面的一些 “能量”（矢量线），使得穿出曲面的矢量线条数减小了。

如果我们再定义一个通量源密度，也就是单位体积内的通量大小。 $\frac{\oiint_S\overrightarrow{A}\sdot \overrightarrow{a_n} \space dS}{V}$
当我们将曲面所包围的体积逐渐缩小的时候，曲面也渐渐逼近通量源，当 $V\to0$时，若极限存在，我们就定义这个极限就是我们所说的散度： $div\overrightarrow{A} = \lim_{V\to0}\frac{\oiint_S\overrightarrow{A}\sdot \overrightarrow{a_n} \space dS}{V}$
这就是散度的定义。说明：散度也是一个标量！

但是，在应用过程中，使用定义式直接计算散度相当麻烦，我们下面给出一个更好用的式子：
先看下面的情况：

我们看这个长方体的最左下角的 $M$，定义 $M(x, y, z)$，长方体的长宽高分别是 $△y, △x, △z$

在 $M$ 点处的矢量为： $\overrightarrow{A} = A_x\overrightarrow{a_x}+A_y\overrightarrow{a_y}+A_z\overrightarrow{a_z}$ 这里特别注意： $A_x, A_y,A_z$都是 $(x,y,z)$ 三者的函数！

我们下面先看看长方体前面的通量： $\oiint_{S1}\overrightarrow{A}\sdot \overrightarrow{a_{front}} dS = \oiint_{S1}A_xdS = A_x(x+△x, y, z)△y△z$
下面，我们回忆一下泰勒公式是怎么用的，下面是 $f(x)$ 在 $x_0$ 处的泰勒展开： $f(x) = \frac{f(x_0)}{0!} + \frac{f'(x_0)}{1!}(x-x_0) + \frac{f''(x_0)}{2!}(x-x_0)^2 + \cdots$
那么，类似地使用变量代换，将上式的 $x$ 代换成 $x+△x$， $x_0$ 换成 $x$， $f()$函数使用 $A_x()$替换，得： $A_x(x+△x,y,z) =A_x(x,y,z)+\frac{\partial A_x(x,y,z)}{\partial x}△x + \frac{1}{2}\frac{\partial^2 A_x(x,y,z)}{\partial x^2}△x^2+\cdots$
因此，我们可以得到一个近似表达： $A_x(x+△x,y,z) ≈ A_x(x,y,z)+\frac{\partial A_x(x,y,z)}{\partial x}△x$

因此，前面的净通量就近似表示成： $\oiint_{S1}\overrightarrow{A}\sdot \overrightarrow{a_{front}} dS ≈A_x(x,y,z)△y△z+\frac{\partial A_x(x,y,z)}{\partial x}△x△y△z$
那么，我们再看看后面得通量：由于 $A_x\overrightarrow{a_x}$ 的方向是沿着 $x$ 轴的正方向，因此与 $\overrightarrow{a_{back}}$ 的方向相反，那么得到的通量结果是： $\oiint_{S2}\overrightarrow{A}\sdot \overrightarrow{a_{back}} dS = -A_x(x,y,z)△y△z$

那么，我们就可以得到前后两个面的净通量： $\begin{aligned} Φ_{front} + Φ_{back} &= A_x(x,y,z)△y△z+\frac{\partial A_x(x,y,z)}{\partial x}△x△y△z - A_x(x,y,z)△y△z\\ &=\frac{\partial A_x(x,y,z)}{\partial x}△x△y△z \end{aligned}$

那么，如果我们求出前后左右上下六个面的净通量，就可以表示成： $Φ_{total} = \frac{\partial A_x(x,y,z)}{\partial x}△x△y△z + \frac{\partial A_y(x,y,z)}{\partial y}△x△y△z + \frac{\partial A_z(x,y,z)}{\partial z}△x△y△z$
令体积微元 $△V = △x△y△z$，因此得到闭合曲面净通量表达式： $Φ_{total} = \frac{\partial A_x(x,y,z)}{\partial x}△V + \frac{\partial A_y(x,y,z)}{\partial y}△V + \frac{\partial A_z(x,y,z)}{\partial z}△V$
把它重新带入散度的定义式，我们就可以得到散度的计算公式： $\begin{aligned} div\overrightarrow{A} &= \frac{\partial A_x(x,y,z)}{\partial x} + \frac{\partial A_y(x,y,z)}{\partial y} + \frac{\partial A_z(x,y,z)}{\partial z}\\ &=\frac{\partial A_x}{\partial x} + \frac{\partial A_y}{\partial y} + \frac{\partial A_z}{\partial z} \end{aligned}$

1. $div\overrightarrow{A} > 0$：则表示该点处有一个正源（发射矢量线）
2. $div\overrightarrow{A} < 0$：则表示该点处有一个负源（吸收矢量线）
3. $div\overrightarrow{A} = 0$：则表示该点没有场源

下面我们定义一个以后非常常用的算子： $\triangledown$算子：(矢量微分算子） $\triangledown = \frac{\partial }{\partial x}\overrightarrow{a_x} + \frac{\partial}{\partial y}\overrightarrow{a_y} + \frac{\partial }{\partial z}\overrightarrow{a_z}$

因此，散度就可以表示成： $div\overrightarrow{A} = \triangledown \sdot \overrightarrow{A}$，散度表示矢量场内一点的吸收或者辐射程度

2.3 高斯散度的定理

三、矢量场的旋度

3.1 先从环量说起：

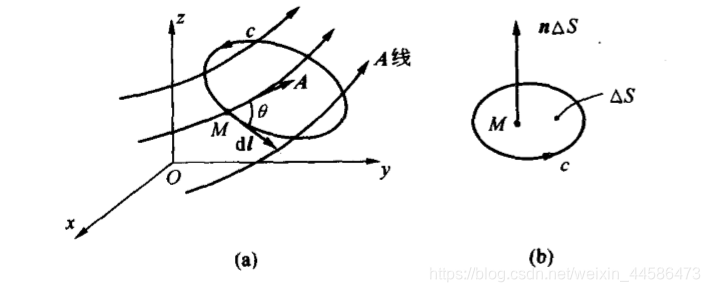
先看看下面的 （a）图，考虑这样一个 $\overrightarrow{A}$ 的矢量场。我们举一个具体的例子：比如说这个一个“风”场，里面每一点的向量的方向代表该点处风力的方向，矢量长度代表该点风力大小。

假如这是由龙卷风组成的强大的场，那么试想一下在这个风暴场里面如果有一个飘零的线圈 $c$，我们可以想象得出来，这个线圈将会收到风力的影响而旋转。那么，如何描述这个线圈 $c$ 所受到的风力大小呢？

我们先从线圈的一个点开始计算：

假设在线圈上一点 $M$，这个点处线圈的方向是 $\overrightarrow{dl}$，风力场在 M 点的矢量方向是 $\overrightarrow{A}$，我们知道，只有切线上的力会导致物体旋转，因此，我们也考虑风力在切线方向的作用： $\overrightarrow{A}$ 在 $\overrightarrow{dl}$ 方向上的投影恰好就是风力在切线方向的大小。

因此，在这一个点 M 上，所受到的风力大小就是： $\overrightarrow{A}\sdot \overrightarrow{dl}$
那么，整个线圈收到的风力大小就是： $\oint_c\overrightarrow{A}\sdot \overrightarrow{dl}$

而其实，如果我们假设这个线圈 $c$ 内部存在一个涡旋源，我们现在还想研究这个涡旋源的强度：

因此，和推导散度类似的办法，假设线圈的面积是 S，如果令 S 无限趋近于0，就可以缩到如图（b）所示的一个点 M，我们有： $\lim_{S\to 0}\frac{\oint_c\overrightarrow{A}\sdot \overrightarrow{dl}}{S}$
这个叫做矢量场 $\overrightarrow{A}$ 在点 M 处沿着方向 $\overrightarrow{n}$ 处的环量面密度。

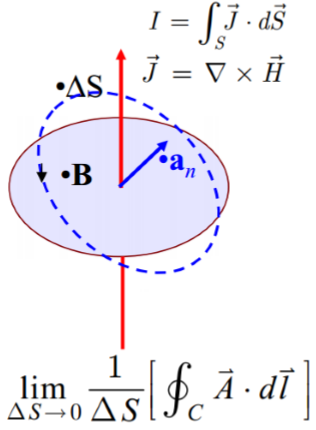
欸？？？按照类比的思路，这里的形式不应该是旋量吗？——但是你别忘了，旋量是一个矢量，它还有方向。开始，经过 M 点的平面有无穷多个，那么方向也就是无穷多个。显然不符合旋量的定义。

如图，假设我们的磁场 $\overrightarrow{B}$ 的方向是沿着竖直轴逆时针旋转的，那么经过中心点取的一个平面，假设这个平面和磁场方向平行，那么 $\overrightarrow{B}$ 在该点处沿着该面方向的环量面密度最大。

因此，我们定义环量面密度最大的时候，环量面密度的模值就是旋量的模值，该环线所围的面积的法向就是旋量的方向。记为： $rot\overrightarrow{A}$

公式就直接给出来： $rot\overrightarrow{A} = \triangledown × \overrightarrow{A}$
即： $rot\overrightarrow{A} = \triangledown × \overrightarrow{A} = \begin{bmatrix} \overrightarrow{a_x} & \overrightarrow{a_y} & \overrightarrow{a_z}\\ \\ \frac{\partial }{\partial x} & \frac{\partial }{\partial x} & \frac{\partial }{\partial x}\\ \\ A_x & A_y & A_Z \end{bmatrix}$

四、梯度、旋度、散度的关系

1. 旋度的散度等于0： $\triangledown \sdot (\triangledown ×\overrightarrow{A}) = 0$
2. 梯度的旋度等于0： $\triangledown × (\triangledown u) = 0$

在这篇 $Blog$ 的最后，再简单说明一个问题： $\triangledown$ 这个算子叫做”矢量微分算子”，也就是说，它既具有矢量的性质，又具有微分的性质（比如复合函数求导法则），我们举两个例子：
【1】 $\triangledown{(uv)}$，这时， $\triangledown$ 具有微分的性质，我们可以看成是对 $uv$ 求导，因为 $uv$ 是一个复合函数，因此就有： $u\triangledown{v} + v\triangledown{u}$

【2】因为向量有下面这个性质： $\overrightarrow{A}\sdot (\overrightarrow{B} × \overrightarrow{C}) = \overrightarrow{B}\sdot (\overrightarrow{A} × \overrightarrow{C}) = \overrightarrow{C}\sdot (\overrightarrow{A} × \overrightarrow{B})$
所以， $\triangledown$ 也有这样的性质： $\triangledown\sdot (\overrightarrow{B} × \overrightarrow{C}) = \overrightarrow{B}\sdot (\triangledown × \overrightarrow{C}) = \overrightarrow{C}\sdot (\triangledown × \overrightarrow{B})$
这时我们要把 $\triangledown$ 当成矢量看待。