听说这年头博客和github跟名片一样?那我干脆把笔记记在博客好了,反正云上笔记也不容易丢。课程跟的是唐宇迪的人工智能必备数学基础,主要记录一些自己的理解和搜集的有助于理解的资料,方便回顾时迅速get到要点。网课CSDN学院 ,网易云课堂 和腾讯课堂 都有(mai bu qi de hua dao ban ye you),鼓励各位支持正版哈,授课老师属于少数的不废话的好老师。回归正题,研究ML(机器学习)、DL(深度学习)方面的童鞋没有数学支撑的话读论文或者搞创新都是很吃力的,磨刀不误砍柴工。
y
=
f
(
x
)
x
:
自
变
量
y
:
因
变
量
y = f(x) x:自变量 y:因变量
y = f ( x ) x : 自 变 量 y : 因 变 量
函
数
值
表
达
形
式
:
y
0
=
y
∣
x
=
x
0
=
f
(
x
0
)
函数值表达形式:y_0 = y\mid_x=x_0 = f(x_0)
函 数 值 表 达 形 式 : y 0 = y ∣ x = x 0 = f ( x 0 )
函
数
俩
种
表
达
式
:
函数俩种表达式:
函 数 俩 种 表 达 式 :
显
函
数
y
=
x
2
+
1
显函数 y = x^2+1
显 函 数 y = x 2 + 1
隐
函
数
F
(
x
,
y
)
=
0
即
x
2
−
y
+
1
=
0
隐函数 F(x, y) = 0 即 x^2-y+1 = 0
隐 函 数 F ( x , y ) = 0 即 x 2 − y + 1 = 0
偶
函
数
:
f
(
−
x
)
=
f
(
x
)
偶函数:f(-x) = f(x)
偶 函 数 : f ( − x ) = f ( x )
奇
函
数
:
f
(
−
x
)
=
−
f
(
x
)
奇函数:f(-x) = -f(x)
奇 函 数 : f ( − x ) = − f ( x )
周
期
性
:
f
(
x
+
T
)
=
f
(
x
)
周期性:f(x+T) = f(x)
周 期 性 : f ( x + T ) = f ( x )
单
调
性
:
单调性:
单 调 性 :
数列 :u1 ,u2 ,u3 ,…,un ,… 其中un 叫做通项
∞
\infty
∞
趋近符号含义
x
→
x
0
:
当
x
从
x
0
两
侧
趋
近
于
x
0
时
x → x_0:当x从x_0两侧趋近于x_0时
x → x 0 : 当 x 从 x 0 两 侧 趋 近 于 x 0 时
x
→
x
0
+
:
当
x
从
x
0
右
侧
趋
近
于
x
0
时
x → x_0^+:当x从x~0~右侧趋近于x_0时
x → x 0 + : 当 x 从 x 0 右 侧 趋 近 于 x 0 时
x
→
x
0
−
:
当
x
从
x
0
左
侧
趋
近
于
x
0
时
x → x_0^-:当x从x~0~左侧趋近于x_0时
x → x 0 − : 当 x 从 x 0 左 侧 趋 近 于 x 0 时
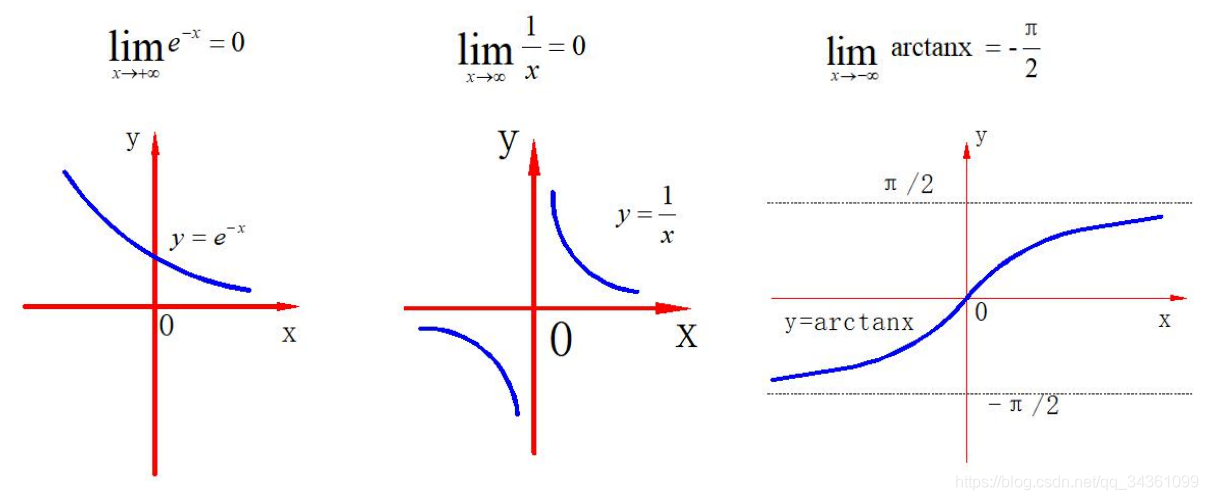
极限
无穷小
lim
Δ
x
→
∞
1
x
=
0
,
则
1
x
是
x
→
∞
时
的
无
穷
小
\lim_{\Delta x\to \infty}\frac{1}{x}=0,则\frac{1}{x}是x\rightarrow\infty时的无穷小
lim Δ x → ∞ x 1 = 0 , 则 x 1 是 x → ∞ 时 的 无 穷 小
lim
Δ
x
→
2
(
3
x
−
6
)
=
0
,
则
3
x
−
6
是
x
→
2
时
的
无
穷
小
\lim_{\Delta x\to 2}(3x-6)=0,则3x-6是x\rightarrow2时的无穷小
lim Δ x → 2 ( 3 x − 6 ) = 0 , 则 3 x − 6 是 x → 2 时 的 无 穷 小
①无限个无穷小之和不一定是无穷小。
lim
n
→
∞
(
1
n
2
+
2
n
2
+
…
+
n
n
2
)
=
lim
n
→
∞
n
(
n
+
1
)
2
n
2
=
lim
n
→
∞
n
+
1
2
n
=
1
2
\lim_{n\to\infty}(\frac{1}{n^2}+\frac{2}{n^2}+…+\frac{n}{n^2})=\lim_{n\to\infty}\frac{\frac{n(n+1)}{2}}{n^2}=\lim_{n\to\infty}\frac{n+1}{2n}=\frac{1}{2}
lim n → ∞ ( n 2 1 + n 2 2 + … + n 2 n ) = lim n → ∞ n 2 2 n ( n + 1 ) = lim n → ∞ 2 n n + 1 = 2 1
②无穷小的商不一定是无穷小。
lim
x
→
0
x
2
x
=
1
2
lim
x
→
0
x
2
2
x
=
0
lim
x
→
0
2
x
x
2
=
∞
\lim_{x\to0}\frac{x}{2x}=\frac{1}{2} \lim_{x\to0}\frac{x^2}{2x}=0 \lim_{x\to0}\frac{2x}{x^2}=\infty
lim x → 0 2 x x = 2 1 lim x → 0 2 x x 2 = 0 lim x → 0 x 2 2 x = ∞
③无穷小的比较
lim
x
→
x
0
α
(
x
)
=
0
lim
x
→
x
0
β
(
x
)
=
0
\lim_{x\to x_0}\alpha(x)=0 \lim_{x\to x_0}\beta(x)=0
lim x → x 0 α ( x ) = 0 lim x → x 0 β ( x ) = 0
l
i
m
x
→
x
0
α
(
x
)
β
(
x
)
=
0
,
则
α
比
β
高
阶
lim_{x\to x_0}\frac{\alpha(x)}{\beta(x)}=0,则\alpha比\beta高阶
l i m x → x 0 β ( x ) α ( x ) = 0 , 则 α 比 β 高 阶
l
i
m
x
→
x
0
α
(
x
)
β
(
x
)
=
∞
,
则
α
比
β
低
阶
lim_{x\to x_0}\frac{\alpha(x)}{\beta(x)}=\infty,则\alpha比\beta低阶
l i m x → x 0 β ( x ) α ( x ) = ∞ , 则 α 比 β 低 阶
l
i
m
x
→
x
0
α
(
x
)
β
(
x
)
=
C
≠
0
,
则
α
与
β
同
阶
lim_{x\to x_0}\frac{\alpha(x)}{\beta(x)}=C≠0,则\alpha与\beta同阶
l i m x → x 0 β ( x ) α ( x ) = C ̸ = 0 , 则 α 与 β 同 阶
设
函
数
f
(
x
)
在
点
x
0
的
某
邻
域
内
有
定
义
,
如
果
当
自
变
量
的
改
变
量
△
x
趋
近
于
零
时
,
相
应
函
数
的
改
变
量
△
y
也
趋
近
于
零
,
则
称
y
=
f
(
x
)
在
点
x
0
处
连
续
设函数f (x)在点x_0的某邻域内有定义,如果当自变量的改变量△x趋近于 零时,相应函数的改变量△y也趋近于零,则称y = f (x)在点 x_0处连续
设 函 数 f ( x ) 在 点 x 0 的 某 邻 域 内 有 定 义 , 如 果 当 自 变 量 的 改 变 量 △ x 趋 近 于 零 时 , 相 应 函 数 的 改 变 量 △ y 也 趋 近 于 零 , 则 称 y = f ( x ) 在 点 x 0 处 连 续 条件
函数在该点处有定义
函数在该点处极限存在
极限值等于函数值
如
果
平
均
变
化
率
的
极
限
存
在
lim
x
→
0
Δ
x
Δ
y
=
lim
x
→
0
f
(
x
0
+
Δ
x
)
−
f
(
x
0
)
Δ
x
如果平均变化率的极限存在\lim_{x\to 0}\frac{\Delta x}{\Delta y}=\lim_{x\to 0}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}
如 果 平 均 变 化 率 的 极 限 存 在 lim x → 0 Δ y Δ x = lim x → 0 Δ x f ( x 0 + Δ x ) − f ( x 0 )
则
称
此
极
限
为
函
数
y
=
f
(
x
)
在
点
x
0
处
的
导
数
,
f
′
(
x
0
)
,
y
′
∣
x
=
x
0
,
d
y
d
x
∣
x
=
x
0
,
d
f
(
x
)
d
x
∣
x
=
x
0
则称此极限为函数y=f(x)在点x_0处的导数,f'(x_0),y'\mid_{x=x_0},\frac{dy}{dx}\mid_{x=x_0},\frac{df(x)}{dx}\mid_{x=x_0}
则 称 此 极 限 为 函 数 y = f ( x ) 在 点 x 0 处 的 导 数 , f ′ ( x 0 ) , y ′ ∣ x = x 0 , d x d y ∣ x = x 0 , d x d f ( x ) ∣ x = x 0
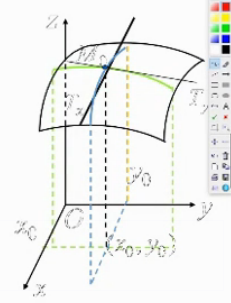
设
函
数
z
=
f
(
x
,
y
)
在
点
(
x
0
,
y
0
)
的
某
个
邻
域
内
有
定
义
,
设函数z=f(x,y)在点(x_0,y_0)的某个邻域内有定义,
设 函 数 z = f ( x , y ) 在 点 ( x 0 , y 0 ) 的 某 个 邻 域 内 有 定 义 ,
定
y
=
y
0
定y=y_0
定 y = y 0
,
一
元
函
数
f
(
x
,
y
0
)
在
点
x
=
x
0
处
可
导
,
即
极
限
lim
Δ
x
→
0
f
(
x
0
+
Δ
x
,
y
0
)
−
f
(
x
0
,
y
0
)
Δ
x
=
A
,
则
称
A
为
函
数
:
z
=
f
(
x
,
y
)
在
点
(
x
0
,
y
0
)
处
关
于
自
变
量
x
的
偏
导
数
,
记
作
f
x
(
x
0
,
y
0
)
或
∂
z
∂
x
∣
x
=
x
0
,
∂
f
∂
x
∣
x
=
x
0
,
Z
x
∣
x
=
x
0
,一元函数f(x,y_0)在点x=x_0处可导,即极限\lim_{\Delta x\to 0}\frac{f(x_0+\Delta x,y_0)-f(x_0,y_0)}{\Delta x}=A,则称A为函数:z=f(x,y)在点(x_0,y_0)处关于自变量x的偏导数,记作f_x(x_0,y_0)或\frac{\partial z}{\partial x}\mid_{x=x_0},\frac{\partial f}{\partial x}\mid_{x=x_0},Z_x\mid_{x=x_0}
, 一 元 函 数 f ( x , y 0 ) 在 点 x = x 0 处 可 导 , 即 极 限 lim Δ x → 0 Δ x f ( x 0 + Δ x , y 0 ) − f ( x 0 , y 0 ) = A , 则 称 A 为 函 数 : z = f ( x , y ) 在 点 ( x 0 , y 0 ) 处 关 于 自 变 量 x 的 偏 导 数 , 记 作 f x ( x 0 , y 0 ) 或 ∂ x ∂ z ∣ x = x 0 , ∂ x ∂ f ∣ x = x 0 , Z x ∣ x = x 0
几何意义
∂
∂
x
f
(
x
,
y
0
)
∣
x
=
x
0
是
曲
线
y
=
{
z
=
f
(
x
,
y
)
y
=
y
0
在
点
M
0
处
的
切
线
M
0
T
x
对
x
轴
的
斜
率
\frac{\partial}{\partial x}f(x,y_0)\mid_{x=x0} 是曲线 y =\begin{cases} z=f (x,y)\\ y=y_0 \end{cases}在点M_0处的切线M_0T_x对x轴的斜率
∂ x ∂ f ( x , y 0 ) ∣ x = x 0 是 曲 线 y = { z = f ( x , y ) y = y 0 在 点 M 0 处 的 切 线 M 0 T x 对 x 轴 的 斜 率
e
g
.
求
f
(
x
,
y
)
=
x
2
+
3
x
y
+
y
2
在
点
(
1
,
2
)
处
的
偏
导
数
eg.求f(x,y)=x^2+3xy+y^2在点(1,2)处的偏导数
e g . 求 f ( x , y ) = x 2 + 3 x y + y 2 在 点 ( 1 , 2 ) 处 的 偏 导 数
f
x
(
x
,
y
)
=
2
x
+
3
y
f
x
(
1
,
2
)
=
8
f_x(x,y)=2x+3y f_x(1,2)=8
f x ( x , y ) = 2 x + 3 y f x ( 1 , 2 ) = 8
f
y
(
x
,
y
)
=
3
x
+
2
y
f
y
(
1
,
2
)
=
7
f_y(x,y)=3x+2y f_y(1,2)=7
f y ( x , y ) = 3 x + 2 y f y ( 1 , 2 ) = 7
l
l
l
z
=
f
(
x
,
y
)
z=f(x,y)
z = f ( x , y )
∂
f
∂
l
=
lim
ρ
→
0
f
(
x
+
Δ
x
,
y
+
Δ
y
)
−
f
(
x
,
y
)
ρ
=
Δ
x
2
+
Δ
y
2
=
∂
f
∂
x
cos
ψ
+
∂
f
∂
y
sin
ψ
\frac{\partial f}{\partial l}=\lim_{\rho\to0}\frac{f(x+\Delta x,y+\Delta y)-f(x,y)}{\rho=\sqrt{\Delta x^2+\Delta y^2}}=\frac{\partial f}{\partial x}\cos \psi+\frac{\partial f}{\partial y}\sin \psi
∂ l ∂ f = lim ρ → 0 ρ = Δ x 2 + Δ y 2
f ( x + Δ x , y + Δ y ) − f ( x , y ) = ∂ x ∂ f cos ψ + ∂ y ∂ f sin ψ
方
向
导
数
为
某
一
方
向
向
量
l
所
在
平
面
与
函
数
相
交
形
成
的
曲
线
在
x
0
处
的
导
数
方向导数为某一方向向量l所在平面与函数相交形成的曲线在x_0处的导数
方 向 导 数 为 某 一 方 向 向 量 l 所 在 平 面 与 函 数 相 交 形 成 的 曲 线 在 x 0 处 的 导 数
偏
导
数
是
l
为
坐
标
轴
方
向
的
方
向
导
数
偏导数是l为坐标轴方向的方向导数
偏 导 数 是 l 为 坐 标 轴 方 向 的 方 向 导 数
函数在某点的梯度是一个方向向量(x,y),它的方向等于方向导数最大值取得的方向 一致,其大小正好是最大的方向导数 eg.
2019.1.13 7:28
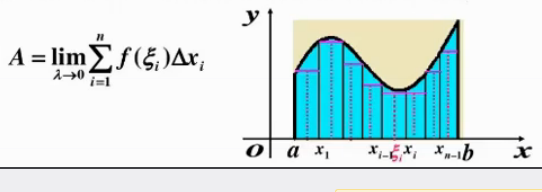
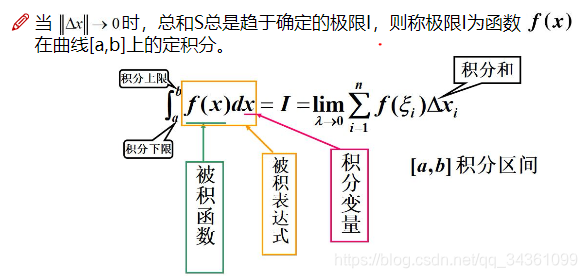
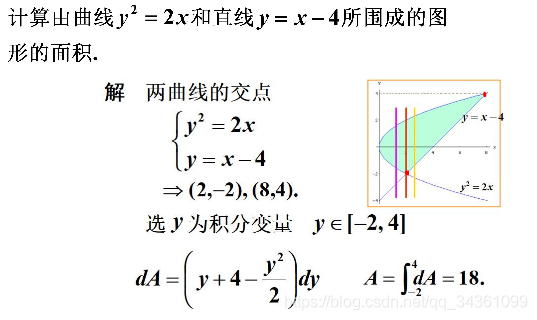
微分矩形:把曲面分为无穷个小矩形,则曲面面积近似于无数个小矩形面积的总和
S
=
∫
a
b
f
(
x
)
Δ
x
(
当
Δ
x
→
0
时
,
ξ
=
f
(
x
)
)
S=\int_a^bf(x)\Delta x (当\Delta x\to0时,\xi=f(x))
S = ∫ a b f ( x ) Δ x ( 当 Δ x → 0 时 , ξ = f ( x ) )
函数意义替换:把
f
(
x
)
f(x)
f ( x )
F
(
x
)
F(x)
F ( x )
F
′
(
x
)
F'(x)
F ′ ( x )
f
(
x
)
在
Δ
x
上
的
积
分
∫
a
b
f
(
x
)
d
x
f(x)在\Delta x上的积分\int_a^bf(x)dx
f ( x ) 在 Δ x 上 的 积 分 ∫ a b f ( x ) d x
=
F
′
(
x
)
的
积
分
∫
a
b
F
′
(
x
)
d
x
=F'(x)的积分\int_a^bF'(x)dx
= F ′ ( x ) 的 积 分 ∫ a b F ′ ( x ) d x
=
∫
a
b
d
y
d
x
⋅
d
x
=
∫
a
b
d
y
(
d
x
→
0
)
=\int_a^b\frac{dy}{dx}\cdot dx=\int_a^bdy (dx\to0)
= ∫ a b d x d y ⋅ d x = ∫ a b d y ( d x → 0 )
≈
函
数
F
(
x
)
在
[
a
,
b
]
区
间
的
增
量
∫
a
b
Δ
y
≈函数F(x)在[a,b]区间的增量\int_a^b\Delta y
≈ 函 数 F ( x ) 在 [ a , b ] 区 间 的 增 量 ∫ a b Δ y
=
F
(
b
)
−
F
(
a
)
=F(b)-F(a)
= F ( b ) − F ( a ) 导函数线下面积=原函数改变量
x
→
0
时
,
Δ
y
=
d
y
x\to0时,\Delta y=dy
x → 0 时 , Δ y = d y
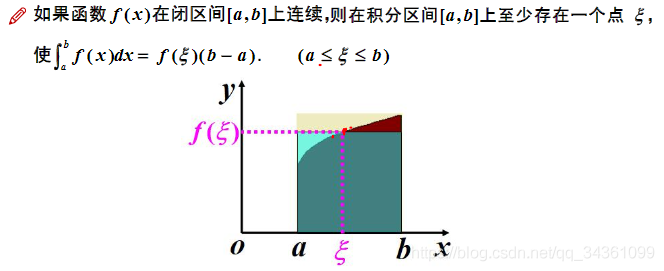
ξ
左
移
,
求
得
的
S
偏
小
ξ
右
移
,
求
得
的
S
偏
大
\xi左移,求得的S偏小 \xi右移,求得的S偏大
ξ 左 移 , 求 得 的 S 偏 小 ξ 右 移 , 求 得 的 S 偏 大
故
必
存
在
ξ
,
使
求
得
的
S
刚
刚
好
故必存在\xi,使求得的S刚刚好
故 必 存 在 ξ , 使 求 得 的 S 刚 刚 好
图
中
f
(
x
)
表
示
上
述
F
(
x
)
图中f(x)表示上述F(x)
图 中 f ( x ) 表 示 上 述 F ( x )
2019.2.4 3:48
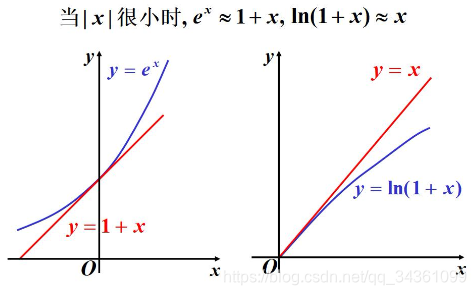
用简单的熟悉的多项式来近似代替复杂的函数
易计算函数值,导数与积分仍是多项式多项式由它的系数完全确定,其系数又由它在一点的函数值及其导数所确定。易计算函数值,导数与积分仍是多项式
多项式由它的系数完全确定,其系数又由它在一点的函数值及其导数所确定。多项式由它的系数完全确定,其系数又由它在一点的函数值及其导数所确定。
当
(
x
−
x
0
)
→
0
时
,
f
(
x
)
=
f
(
x
0
)
+
∫
x
0
x
f
′
(
x
)
(
x
−
x
0
)
≈
f
(
x
0
)
+
f
′
(
x
0
)
(
x
−
x
0
)
当(x-x_0)\to0时,f(x)=f(x_0)+\int_{x_0}^xf'(x)(x-x_0)≈f(x_0)+f'(x_0)(x-x_0)
当 ( x − x 0 ) → 0 时 , f ( x ) = f ( x 0 ) + ∫ x 0 x f ′ ( x ) ( x − x 0 ) ≈ f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 )
P
n
(
x
)
=
f
(
x
0
)
+
f
′
(
x
0
)
(
x
−
x
0
)
+
f
′
′
(
x
0
)
2
!
(
x
−
x
0
)
2
+
…
+
f
(
n
)
(
x
0
)
n
!
(
x
−
x
0
)
n
P_n(x)=f(x_0)+f'(x_0)(x-x_0)+\frac{f''(x_0)}{2!}(x-x_0)^2+…+\frac{f^{(n)}(x0)}{n!}(x-x_0)^n
P n ( x ) = f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) + 2 ! f ′ ′ ( x 0 ) ( x − x 0 ) 2 + … + n ! f ( n ) ( x 0 ) ( x − x 0 ) n
称
为
f
(
x
)
在
x
0
关
于
(
x
−
x
0
)
的
n
阶
泰
勒
多
项
式
称为f(x)在x_0关于(x-x_0)的n阶泰勒多项式
称 为 f ( x ) 在 x 0 关 于 ( x − x 0 ) 的 n 阶 泰 勒 多 项 式
f
(
a
+
Δ
x
)
=
f
(
a
)
+
∫
a
a
+
Δ
x
f
′
(
x
)
d
x
(
牛
顿
—
莱
布
尼
茨
公
式
)
f(a+\Delta x)=f(a)+\int_a^{a+\Delta x}f'(x)dx (牛顿—莱布尼茨公式)
f ( a + Δ x ) = f ( a ) + ∫ a a + Δ x f ′ ( x ) d x ( 牛 顿 — 莱 布 尼 茨 公 式 )
=
f
(
a
)
+
f
′
(
a
)
Δ
x
+
f
′
′
(
a
)
2
Δ
x
2
+
∫
0
Δ
x
∫
a
a
+
t
∫
a
a
+
t
1
f
′
′
′
(
x
)
d
x
d
x
d
t
(
换
元
x
=
a
+
t
)
=f(a)+f'(a)\Delta x+\frac{f''(a)}{2}\Delta x^2+\int_0^{\Delta x}\int_a^{a+t}\int_a^{a+t_1}f'''(x)dxdxdt (换元x=a+t)
= f ( a ) + f ′ ( a ) Δ x + 2 f ′ ′ ( a ) Δ x 2 + ∫ 0 Δ x ∫ a a + t ∫ a a + t 1 f ′ ′ ′ ( x ) d x d x d t ( 换 元 x = a + t ) 这篇博客
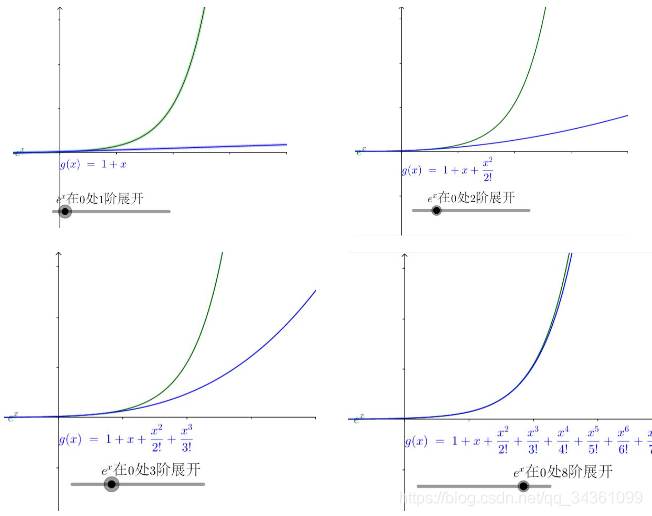
任意多阶可导函数可被展开为泰勒多项式以简化函数表达
指定
x
0
=
0
的
泰
勒
公
式
x_0=0的泰勒公式
x 0 = 0 的 泰 勒 公 式
f
(
x
)
=
f
(
0
)
+
f
′
(
x
)
x
+
f
′
′
(
0
)
2
!
x
2
+
…
+
f
(
n
)
(
0
)
n
!
x
n
+
f
(
n
+
1
)
(
θ
x
)
(
n
+
1
)
!
x
n
+
1
(
0
<
θ
<
1
)
f(x)=f(0)+f'(x)x+\frac{f''(0)}{2!}x^2+…+\frac{f^{(n)}(0)}{n!}x^n+\frac{f^{(n+1)(\theta x)}}{(n+1)!}x^{n+1}(0<\theta<1)
f ( x ) = f ( 0 ) + f ′ ( x ) x + 2 ! f ′ ′ ( 0 ) x 2 + … + n ! f ( n ) ( 0 ) x n + ( n + 1 ) ! f ( n + 1 ) ( θ x ) x n + 1 ( 0 < θ < 1 )
f
(
x
)
≈
f
(
0
)
+
f
′
(
x
)
x
+
f
′
′
(
0
)
2
!
x
2
+
…
+
f
(
n
)
(
0
)
n
!
x
n
f(x)≈f(0)+f'(x)x+\frac{f''(0)}{2!}x^2+…+\frac{f^{(n)}(0)}{n!}x^n
f ( x ) ≈ f ( 0 ) + f ′ ( x ) x + 2 ! f ′ ′ ( 0 ) x 2 + … + n ! f ( n ) ( 0 ) x n
多阶导数的意义
f
(
x
)
=
e
x
f(x)=e^x
f ( x ) = e x
指数项的意义
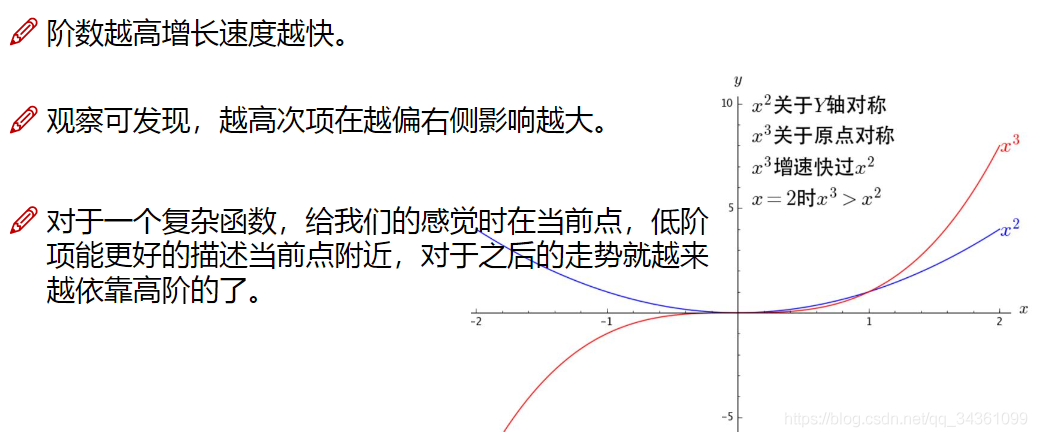
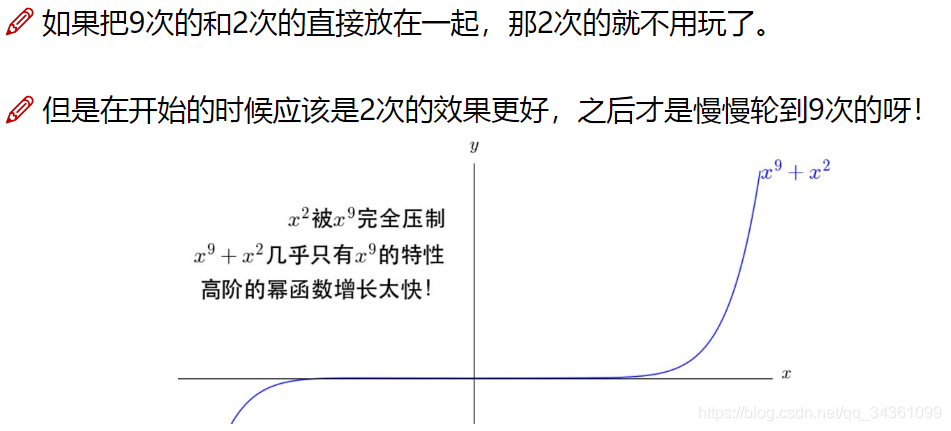
控制x小时低阶数大权重,x大时高阶数大权重(初始系数)
函
数
:
f
(
x
,
y
)
约
束
:
g
(
x
,
y
)
=
C
求
满
足
约
束
条
件
的
函
数
极
值
函数:f(x,y) 约束:g(x,y)=C 求满足约束条件的函数极值
函 数 : f ( x , y ) 约 束 : g ( x , y ) = C 求 满 足 约 束 条 件 的 函 数 极 值 二维曲线
g
(
x
,
y
)
=
C
g(x,y)=C
g ( x , y ) = C
z
=
f
(
x
,
y
)
z=f(x,y)
z = f ( x , y ) 二维曲线 )
f
(
x
,
y
)
=
d
(
常
数
)
f(x,y)=d(常数)
f ( x , y ) = d ( 常 数 ) 梯度向量(方向导数取最大值时的
l
l
l 平行(此时梯度可能不相等 )
2019.2.5 17:53
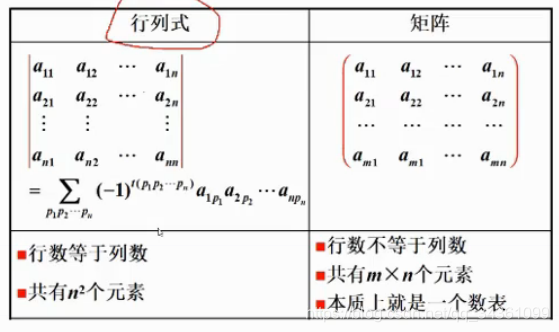
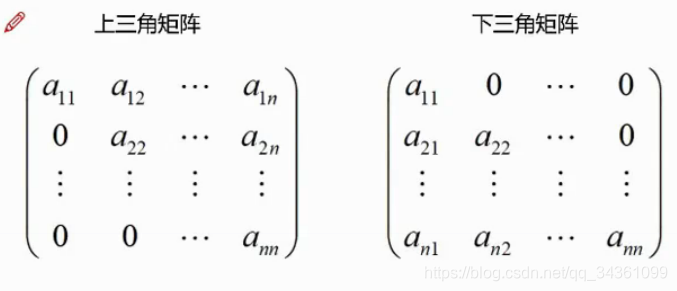
方阵 三角矩阵 对角阵和单位矩阵
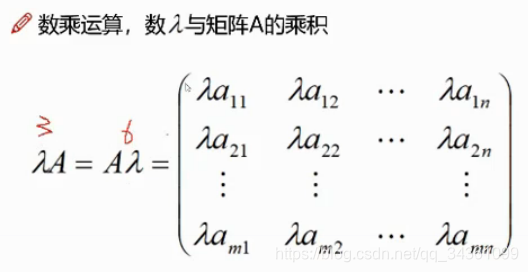
矩阵数乘 矩阵乘法 矩阵结合律
(
A
B
)
C
=
A
(
B
C
)
(AB)C = A(BC)
( A B ) C = A ( B C )
λ
(
A
B
)
=
(
λ
A
)
B
=
A
(
λ
B
)
\lambda (AB)=(\lambda A)B=A(\lambda B)
λ ( A B ) = ( λ A ) B = A ( λ B )
矩阵分配律
A
(
B
+
C
)
=
A
B
+
A
C
A(B+C)=AB+AC
A ( B + C ) = A B + A C
(
B
+
C
)
A
=
B
A
+
C
A
(B+C)A=BA+CA
( B + C ) A = B A + C A
矩阵转置 对称矩阵 逆矩阵
指的矩阵的各行向量的极大线性无关组数即相互不平行的行向量数零向量可看作与任何向量平行 矩阵的行秩=列秩
对应位置相乘后求和 内积的几何意义 图片来源
向量正交 ⇔ 垂直 ⇔ 内积为零
规范正交基
2019.2.6 14:16


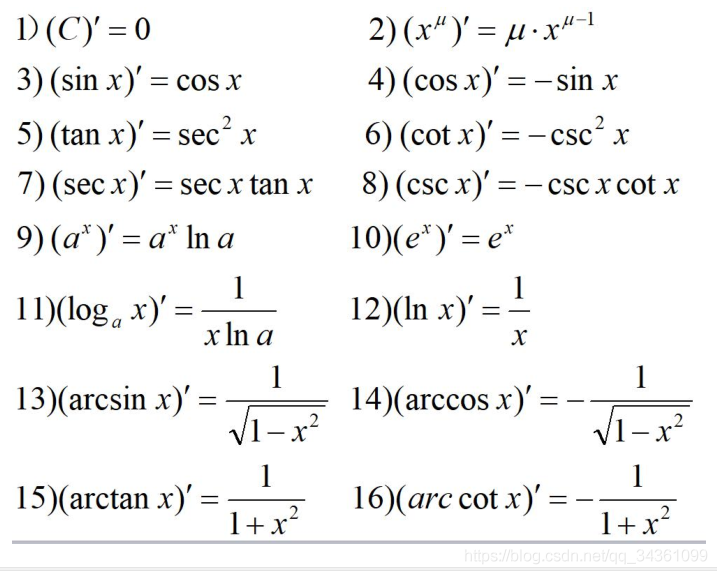

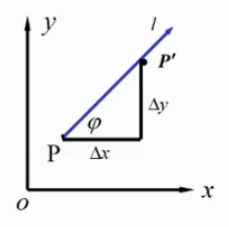 设
为任意一个方向向量
设
为任意一个方向向量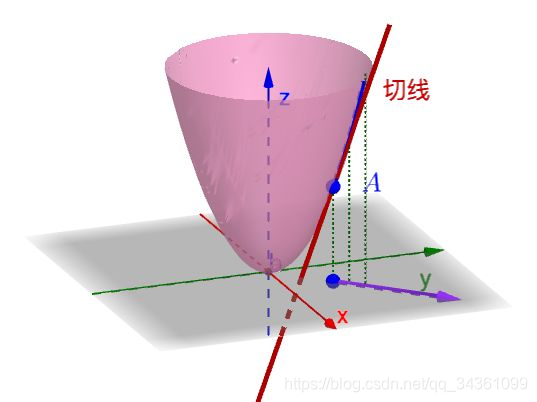















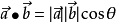 图片来源
图片来源

