通信原理复习笔记（001）

第一章 绪论

1.1 基本概念

• 通信的目的：为了信息交流
• 消息：人感知所获得，如图像文字等
• 信息：获得消息时所消除的不确定性
• 通信系统的一般组成：信息源->发送设备->信道（含噪声源）->接收设备->受信者

1.2 通信系统

1.2.1 模拟信号和数字信号（与数字信号处理中相应的概念不同）

• 模拟信号：（时间，幅值均可离散）只要代表消息的参量取值连续即可
• 数字信号：（时间，幅值均可连续）只要代表消息的参量取值为有限个即可

1.2.2 模拟通信系统与数字通信系统

• 模拟通信系统：利用模拟信号来传递信息的通信系统；
• 数字通信系统：利用数字信号来传递信息的通信系统；信源编码与译码的目的：有效性（降低信息冗余）；信道编码与译码的目的：可靠性（适当增加信息冗余）
• 数字通信系统：
  优点：抗干扰能力强；易于集成；保密性好；易于处理和存储
  缺点：所需带宽大，同步性要求高。

1.3 通信方式

1.3.1 单工、半双工和全双工通信

• 单工通信：消息只能按照通信方到受信方一个方向传输
• 半双工：消息可以双向传输，但不能同时传输
• 双工：消息可以同时进行双向传输

1.3.2 并行与串行传输

• 并行传输：将消息的数字信号码元序列经过多条并行信道同时传输；
  优点：速度快，节省时间
  缺点：成本高
• 串行传输：将消息按照一个一个的码元在一条信道上传输；
  优点：成本低
  缺点：耗时间，速度慢

1.4 信息度量

1.4.1 信息量与其概率成反比

具体值可用I = -log_aP(x)来计算。

• a为2时，上述公式所得结果的单位为比特
• a为e时，单位为奈特
• a为10时，单位为哈莱特

1.4.2 信息源的熵

用H(x)表示，其值为信息源中每个符号的概率与其信息量之积，最后将这些结果进行累加。

1.5 通信系统只要性能指标

	有效性	可靠性
模拟系统	有效传输频带	接收端最终输出的信噪比
数字系统	传输速率（码元传输速率RB，信息传输速率Rb都是和编码方式有关的，要尽可能能提高编码效率）、频带利用率，	误码率（码元数之比）、误信率（比特数之比）

第二章 确知信号

2.1 确知信号类型

• 首先说一下什么是确知信号：确定可知的信号，这些信号不会是随机的：周期、非周期信号等。

2.1.1 按照能量来分

• 能量信号：信号的能量（这里采用信号的平方）在整个时间域：负无穷到正无穷的积分不是无穷大
• 功率信号：信号能量无穷大，但是功率却有限。

2.2 Parseval定理，能谱，功率谱

• Parseval定理：
• 能量信号：由时域所得的信号能量 = 由频域所得的信号能量
  $\int_{-\infty}^{\infty}f^{2}(t)dt=\frac{1}{2 \pi} \int_{-\infty}^{\infty}|F(\omega)|^{2} d \omega$
  其中 $|F(\omega)|^{2}$称为能谱密度
• 功率信号：由时域所得的信号功率 = 由频域所得的信号功率
  $\lim _{T \rightarrow \infty}\frac{1}{T}*\int_{-T/2}^{T/2}f^{2}(t)dt =\lim _{T \rightarrow \infty}\frac{1}{2 \pi} \int_{-\infty}^{\infty}\frac{1}{T}*|F(\omega)|^{2} d \omega$
  其中 $\frac{1}{T}*|F(\omega)|^{2}$称为功率谱密度函数。

2.3 能量信号的自相关函数

• 先上公式 $R(\tau)=\int_{-\infty}^{\infty} s(t) s(t+\tau) d t \quad-\infty<\tau<\infty$
  要与卷积公式相区别，我会专门写一篇文章辨析这个公式，当时我一步一步推的时候，贼有趣。
• 重要的来了：自相关函数实际描述的是信号本身与信号延时 $\tau$后，它们俩的相似程度。
• 能量信号的自相关函数有以下性质：
  R(0)为信号能量
  关于 $\tau$的偶函数
  自相关函数与能量谱密度互为傅里叶变换

2.4 功率信号的自相关函数

• 先上公式
  $R(\tau)=lim_{T \rightarrow \infty}\frac{1}{T}*\int_{-T/2}^{T/2} s(t) s(t+\tau) d t \quad-\infty<\tau<\infty$
  根据自相关函数是表示信号与延时后的信号的相似程度，我们会得到，只有周期信号的自相关函数也是周期的。这条定理要记住，它是判断一个信号是否是周期信号的的一种判断方式。
• 能量信号的自相关函数有以下性质：
  R(0)为信号平均功率
  关于 $\tau$的偶函数
  自相关函数与功率谱密度互为傅里叶变换。

第三章 随机过程

3.1 随机过程的基本概念

• 什么是随机过程？
  事件发生前不可知，但是在发生后就可知了。

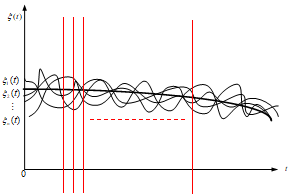
3.1.1 怎样描述随机过程

• 角度1：不同随机试验结果即样本函数的集合
  样本函数：随机过程的一次实现
• 角度2：随机变量的集合
  随机变量：在一个固定的时刻t₁，每一个样本函数均有一个取值，这些取值的集合构成一个随机变量，多个随机变量是按照时间顺序排列的。
  角度1，角度2都可以参考下图：
  

3.1.2 随机过程的分布函数

• 一维分布函数：在某个时刻，样本函数的取值（即一个随机变量）小于x的概率： $F_{1}\left(x_{1}, t_{1}\right)=P\left[\xi\left(t_{1}\right) \leq x_{1}\right]$
  对于x₁求偏导即可得到一维概率密度函数。
• 二维 分布函数：在某两个时刻，样本函数的取值（即一个随机变量）分别小于x₁与·x₂的概率： $F_{2}\left(x_{1}, x_{2} ; t_{1}, t_{2},\right)=P\left\{\xi\left(t_{1}\right) \leq x_{1}, \xi\left(t_{2}\right) \leq x_{2}\right\}$

3.1.3 随机过程的数字特征

• 均值（即数学期望）:这是对于上述的随机过程的分布函数来说的。 $E[\xi(t)]=\int_{-\infty}^{\infty} x f_{1}(x, t) d x$
  我们发现均值是时间t的函数。常用 $a(t)$来表示。如下图：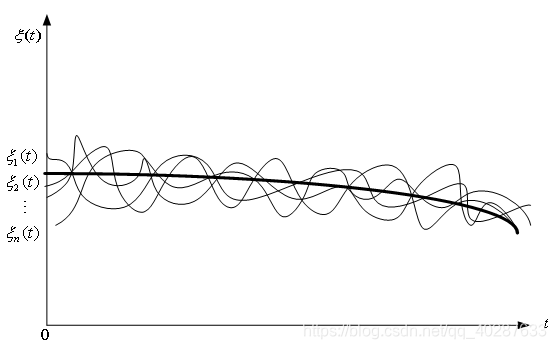
  中间的黑粗线即是 $a(t)$。
• 方差：表示随机过程在某时刻相对于当时的均值的偏离程度。 $D[\xi(t)]=E\left\{[\xi(t)-a(t)]^{2}\right\}$
• 相关函数：表示同一个随机过程的不同随机变量的相关程度。 $\begin{aligned} R\left(t_{1}, t_{2}\right) &=E\left[\xi\left(t_{1}\right) \xi\left(t_{2}\right)\right] \\ &=\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} x_{1} x_{2} f_{2}\left(x_{1}, x_{2} ; t_{1}, t_{2}\right) d x_{1} d x_{2} \end{aligned}$
• 协方差： $\begin{aligned} B\left(t_{1}, t_{2}\right) &=E\left\{\left[\xi\left(t_{1}\right)-a\left(t_{1}\right)\right]\left[\xi\left(t_{2}\right)-a\left(t_{2}\right)\right]\right\} \\ &=\int_{-\infty}^{\infty} \int_{-\infty}^{\infty}\left[x_{1}-a\left(t_{1}\right)\right]\left[x_{2}-a\left(t_{2}\right)\right] f_{2}\left(x_{1}, x_{2} ; t_{1}, t_{2}\right) d x_{1} d x_{2} \end{aligned}$
• 互相关函数：表示两个随机过程的相关程度。 $R_{\xi \eta}\left(t_{1}, t_{2}\right)=E\left[\xi\left(t_{1}\right) \eta\left(t_{2}\right)\right]$
• 我们由上述的相关函数与协方差的公式可以得到它们俩的关系： $B\left(t_{1}, t_{2}\right)=R\left(t_{1}, t_{2}\right)-a\left(t_{1}\right) a\left(t_{2}\right)$

3.2 平稳随机过程

3.2.1定义

• 狭义（严）平稳随机过程
  还是对于分布函数来说：任意维的分布函数具有时不变（信号与系统的概念）的性质。 $\begin{array}{l} f_{n}\left(x_{1}, x_{2}, \cdots, x_{n} ; t_{1}, t_{2}, \cdots, t_{n}\right) \\ =f_{n}\left(x_{1}, x_{2}, \cdots, x_{n} ; t_{1}+\Delta, t_{2}+\Delta, \cdots, t_{n}+\Delta\right) \end{array}$
  其均值为一个常数，与时间无关，且自相关函数只与时间间隔 $\tau$有关
• 广义（宽）平稳随机过程
  满足以下性质即可：
  （1）其均值为一个常数，与时间无关
  （2）自相关函数只与时间间隔 $\tau$有关

3.2.2 各态历经性（又称“遍历性”）

• 这是对于平稳过程的数字特征来说的：
  只需一次实验就可以得到整个平稳过程的数字特征。
• 条件：时间平均 = 集合平均
  （1)一次实验的时间均值等于在3.2.1最后得到的均值
  （2）一次实验的时间自相关函数等于在3.2.1最后得到的自相关函数。
• 最后需要注意：各态历经性可以推出平稳过程，反之不一定成立。

3.2.3 平稳过程的功率谱密度

• 对于任意的功率信号： $P_{f}(f)=\lim _{T \rightarrow \infty} \frac{\left|F_{T}(f)\right|^{2}}{T}$但是对于平稳过程，则要用统计平均的思想： $P_{\xi}(f)=E\left[P_{f}(f)\right]=\lim _{T \rightarrow \infty} \frac{E\left|F_{T}(f)\right|^{2}}{T}$
• 维纳-辛钦关系：
  非周期的功率确知信号自相关函数的傅里叶变换是其功率谱密度。并不是上面所提到的互为傅里叶变换。

3.3 高斯随机过程

分布函数服从正态分布即可。
其具有以下性质：
（1）广义平稳的高斯过程也是狭义的平稳过程；
（2）经过线性系统后仍是高斯过程；
（3）不相关就独立。

3.4 平稳随机过程通过线性系统

• 若输入平稳，输出也平稳。
• 维纳-辛钦定理
  $P_{0}(f)=H^{*}(f) \cdot H(f) \cdot P_{1}(f)=|H(f)|^{2} P_{i}(f)$

3.5 窄带随机过程

3.5.1 定义

• 若随机过程的谱密度集中在中心频率附近相对窄的频带范围内，即满足频带 <<中心频率的条件，且中心频率远离零频率，则称其为窄带随机过程。

3.5.2 同相，正交分量

• 窄带随机过程的表示式
  $\xi(t)=a_{\xi}(t) \cos \left[\omega_{c} t+\varphi_{\xi}(t)\right] \quad, \quad a_{\xi}(t) \geq 0$
  可以拆成 $\xi(t)=\xi_{c}(t) \cos \omega_{c} t-\xi_{s}(t) \sin \omega_{c} t$前者为随机过程的同相分量，后者为正交分量。
• 同相，正交分量的统计特性 $E\left[\xi_{c}(t)\right]=0, \quad E\left[\xi_{s}(t)\right]=0$ $\begin{aligned} &R_{c}(t, t+\tau)=R_{c}(\tau)=R_{s}(\tau)\\ &R_{c s}(t, t+\tau)=R_{c s}(\tau)=-R_{s c}(\tau) \end{aligned}$
• 一个均值为零的窄带平稳高斯过程，它的同相分量和正交分量同样是平稳高斯过程，而且均值为零，方差也相同。此外，在同一时刻上得到的同相与正交分量是互不相关的或统计独立的。其包络的一维分布是瑞利分布，相位的一维分布是均匀分布，并且就一维分布而言，包络与相位是统计独立的。

3.6 白噪声

• 功率谱密度在整个频率轴上为常数。真正“白”的噪声是不存在的，它只是构造的一种理想化的噪声形式。
  实际中，只要噪声的功率谱均匀分布的频率范围远远大于通信系统的工作频带，我们就可以把它视为白噪声。