最优化技术——单纯形法

最优化技术——单纯形法

说明

这个文章的大部分内容（几乎全部）都来自于我最优化课程的课程笔记。主要来源是重庆大学文静老师的PPT，个人主要用于整理、归纳，如果有侵权等问题，我会在第一时间将博客撤销。

单纯形法的流程介绍

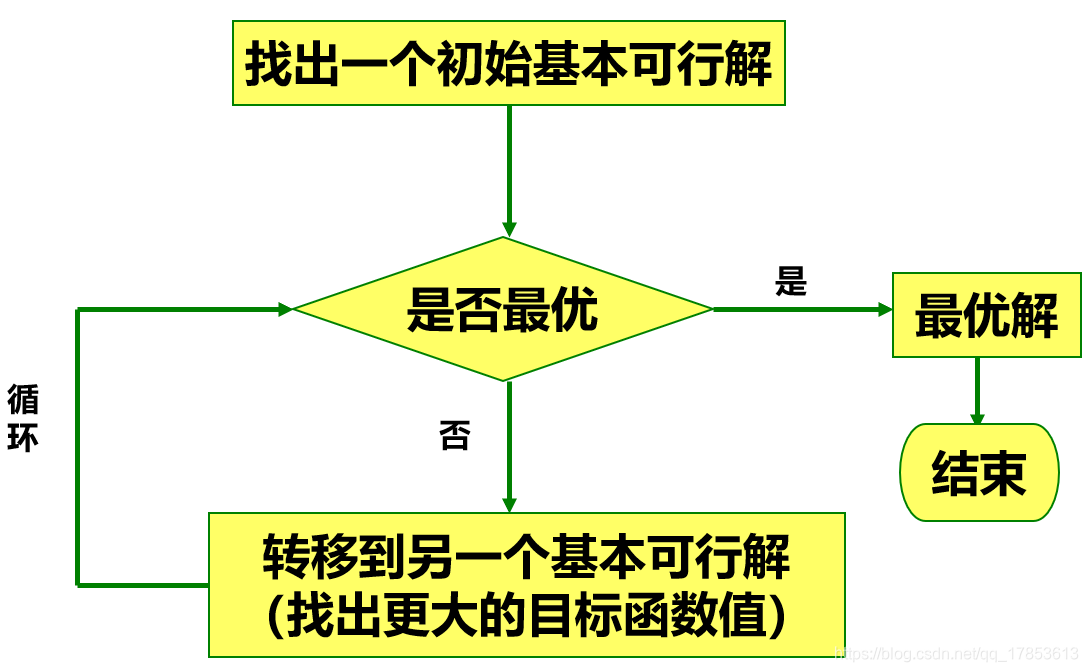
直观的去看这个流程，有一点点像前面的一些函数的优化方法。但是在枚举的过程中，有一些问题值得关注：

• 枚举的起点？
• 如何判断当前已经是最优解了？
• 如何在当前解的前提下找到一个更好的解？

单纯形法的迭代原理

通过一个例子来讲解单纯形法的基本原理

我们这样一个线性规划问题：

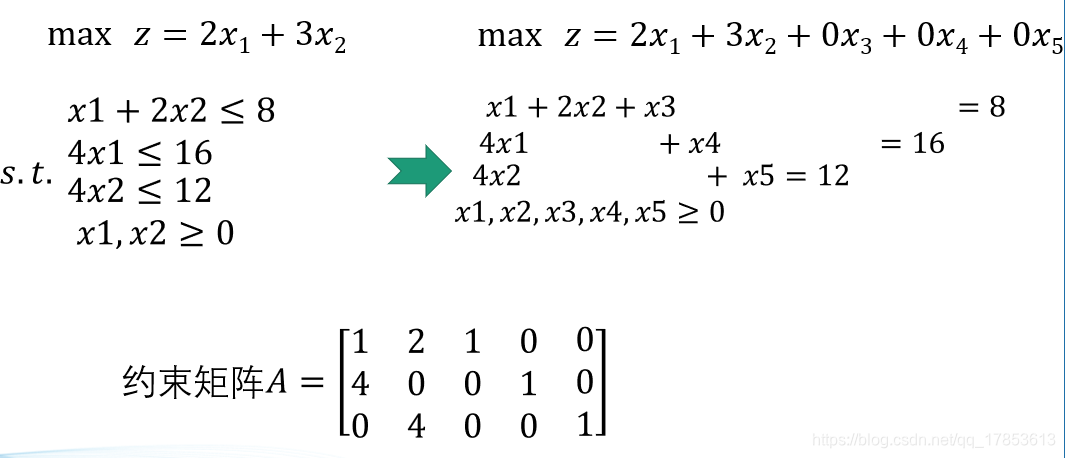
因为这里主要讨论单纯形法，所以我们不再纠结怎么化成标准型。

1. 选择初始基，确定基本可行解

   这里使用的是观察法(我：？？？)，观察系数矩阵中是否含有现成的单位阵，如果有的话就直接用现成的单位阵作为基。

   在这里我们选定的基变量为： $(x_3,x_4,x_5)$

   选定的基矩阵为单位矩阵 $I_3$

   找到的基本可行解：

   $\left[ \begin{matrix}x_B\\x_N \end{matrix} \right] = \left[ \begin{matrix}B^{-1}b\\0 \end{matrix} \right]$

   即： $x_1,x_2,x_3,x_4,x_5 = 0,0,8,16,12$

   Q:为什么要找单位阵?

   A:我们都学过《线性代数》，线代告诉我们，一个矩阵能够被化作单位矩阵和这个矩阵可逆是等价的，有根据上一节讲的，在求解过程中需要对基去逆，所以综上所述，需要找一个单位阵/可以化成单位阵的。

2. 判断当前解是否为最优解

   将基变量使用非基变量表示，使用非基变量表示目标函数。

   $x_3 = 8 - x_1 - 2x_2$

   $x_4 = 16 - 4x_1$

   $x_5 = 12 - 4x_2$

   $Z = 2x_1 +3x_2$

   我们的非基变量向上增加，目标函数 $Z$的值也是增加的，所以说现在的基本可行解的取值不是最优的。那么什么时候它的取值才是最优的呢？

   当非基变量的值增加，而目标函数的值不增加的时候，就是最优的。

   也就是说当目标函数中的系数也就是检验数都小于等于0时，就是最优解，这里包括两种情况：

   • 检验数为0 ： 是最优解，但并不是唯一的最优解，表示存在无数个最优解
   • 检验数为1：是唯一的最优解

3. 如何转到下一个基本可行解

   回到我们的目标函数：

   $Z = 2x_1 + 3 x_2$

   从这个目标函数中我们可以看出， $x_2$对目标函数的贡献比 $x_1$大。要让 $x_2$的取值从0变成正值，所以 $x_2$从非基变量转为基变量，称作进基变量。

   这里就有一个问题，有一个变量从非基变量变成基变量，就意味着会有一个基变量变成非基变量，这个变成非基变量的变量叫做离基变量。

   离基变量的选择：

   这里我们需要回到用非基变量表示基变量的那一步：

   $x_3 = 8 - x_1 - 2x_2$

   $x_4 = 16 - 4x_1$

   $x_5 = 12 - 4x_2$

   那么在挑选离基变量的时候，我们将收敛的最快的（当进基变量增大时，最先到0的）拿出去。

   按照这个方法，我们新的基变量是 $(x_2,x_3,x_4)$，非基变量是： $(x_1,x_5)$

   然后再回到第一步开始检验，直到得到最优解为止。

单纯形表

单纯形表的构建

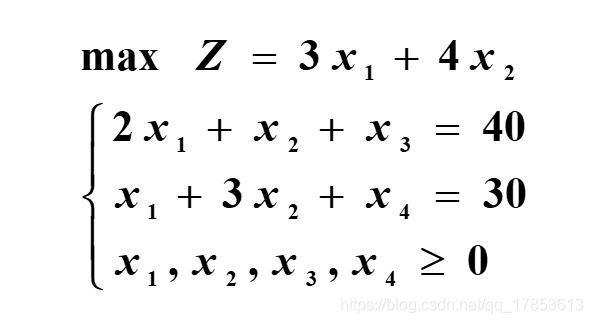
这里我们不再关注怎么加松弛变量之类的问题了

单纯形表中：

• $X_B$：表示当前的基变量，初始挑选单位阵为初始基，构成向量B

• $C_B$：代表当前基变量在目标函数中的系数向量

• $b_j$：代表约束条件的右端的b值

• $c_j$：代表目标函数的系数，在这里 $c= （3，4，0，0）$

• $x_1,x_2...$下面的数字：约束条件的系数矩阵

• $\sigma_j$：检验数， $\sigma_j = c_j-\Sigma c_ia_{ij}$ ，这里的 $a_{ij}$是系数矩阵

  以 $\sigma_1$为例， $\sigma_1 = 3-( 2*0+1*0)=3$

找到入基变量

方法：找检验数最大的，再上一张表里面， $x_2$的检验数最大，所以将作为入基变量

找到出基变量

方法：找 $\theta$，我们顺着上面来，我们现在确定了 $x_2$就是所谓的入基变量，下面，开始计算：

$\theta = \frac{b_j}{x_2}$

在上面的表中， $\theta_3= 40,\theta_4 = 10$

值得注意的是：当 $x_2$的值为负值的时候，就不需要求 $\theta$了。

到此为止，谁的 $\theta$值越小就选谁当出基变量

总体操作

找到入基变量，出基变量之后，列一张新的单纯形表，并且以此往复即可。当所有非基变量都为负数或零时停止，这时最优解就是：基变量取得到的值，非基变量取0.