简介
这就是用来记录我对于《信息学奥赛一本通 · 提高篇》一书中的习题的刷题记录以及学习笔记。
一般分专题来写(全部写一起可能要加载很久...),比如本章就是用来记录贪心的。
再插一句:Loj 真是个不错的 OJ,如果说洛谷是最棒的 OIer 社区,那 Loj 就是最棒的刷题专区。
PS:这里的“最棒的”仅仅指带给我的练习感觉最好,例如画风好康,且仅代表个人意见。
专题介绍:贪心,对于最优解类题目的解决利器,但是往往代码简单却很难想象及证明。(本章中一般会详细证明)
第一题
其实是很简单的贪心,然后贪心套路是显而易见的。
就是按照右端点升序排序,当 其左端点>=上一次选择的右端点 时,ans++。
证明如下:
首先我们假设这 \(N\) 条线段的左右端点分别为 \(a_i,b_i\)。
假设已经排好序,即 \(b_1<b_2<...<b_n\),那么假设 \((b_j<b_i)\),且 \((a_j,b_j)\) 与 \((a_i,b_i)\) 与之前活动不冲突。
同时假设当前已经选择 \((a_j,b_j)\)。
- 若 \((a_j,b_j)\) 与 \((a_i,b_i)\) 互不冲突:即 \(b_j\leq a_i\),那么可以选择 \((a_i,b_i)\)。
- 若 \((a_j,b_j)\) 与 \((a_i,b_i)\) 冲突:即 \(b_j>a_i\),那么因为 \(b_j<b_i\),所以选择 \((a_j,b_j)\) 对后面影响更小。
由此可见,当 \(b_1<b_2<...<b_n\) 时,选择 \(last\_b_j\leq a_i\) 的线段最优。
证毕。
code:
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<iostream>
#include<cstring>
#define N 1010
using namespace std;
int n;
struct node{
int s,f;
}a[N];
int read(){
int x=0,f=1;char c=getchar();
while(c<'0' || c>'9') f=(c=='-')?-1:1,c=getchar();
while(c>='0' && c<='9') x=x*10+c-48,c=getchar();
return x*f;
}
bool cmp(node a,node b){
return a.f<b.f;//按照结束时间升序排序。
}
int main(){
n=read();
for(int i=1;i<=n;i++){
a[i].s=read();a[i].f=read();
}
sort(a+1,a+n+1,cmp);//排序。
int ans=1,jl=a[1].f;//jl 用来记录上一次的右端点。
for(int i=2;i<=n;i++){
if(a[i].s>=jl){//贪心策略。
ans++;jl=a[i].f;
}
}
printf("%d\n",ans);
return 0;
}
第二题
区间选点覆盖问题,显然是挑选靠后的点更优。做法如下:
- 将每个区间按照结束点从小到大排列。
- 对每个区间依次处理:
- 得到整个区间的点数。
- 若 区间点数>要求点数,
continue。 - 否则从后往前在没有树的位置上添加 要求点数-区间点数 个点。
证明如下:
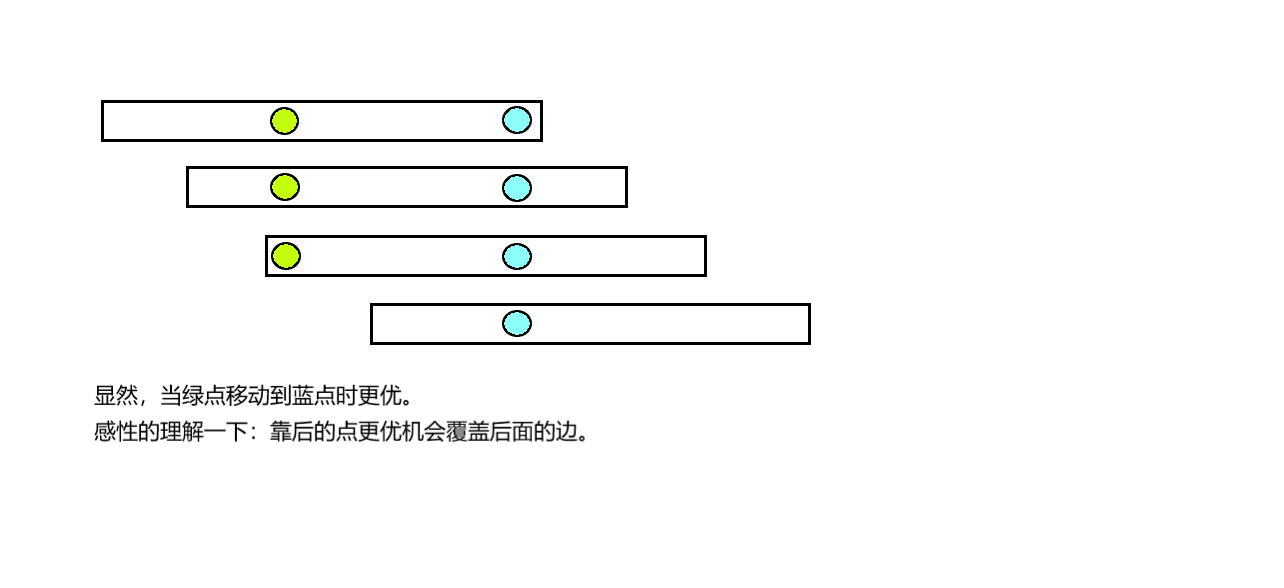
所以...就是酱紫啦。
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<iostream>
#define N 30010
#define M 5010
using namespace std;
int n,m;
bool flag[N];
struct node{
int l,r,s;
}a[M];
int read(){
int x=0,f=1;char c=getchar();
while(c<'0' || c>'9') f=(c=='-')?-1:1,c=getchar();
while(c>='0' && c<='9') x=x*10+c-48,c=getchar();
return x*f;
}
bool cmp(node a,node b){
return a.r<b.r;
}
int main(){
memset(flag,false,sizeof(flag));
n=read();m=read();
for(int i=1;i<=m;i++)
a[i].l=read(),a[i].r=read(),a[i].s=read();
sort(a+1,a+m+1,cmp);
int ans=0;
for(int i=1;i<=m;i++){
int l=a[i].l,r=a[i].r,sum=0;
for(int j=l;j<=r;j++) if(flag[j]) sum++;
if(sum>=a[i].s) continue;
sum=a[i].s-sum;
ans+=sum;
for(int j=r;j>=l;j--){
if(!sum) break;
if(!flag[j]){flag[j]=true;sum--;}
}
}
printf("%d\n",ans);
return 0;
}
第三题
挺好的题目。
首先排除掉 \(r\leq W\) 的点(因为它连自己正下方的范围都覆盖不了),计算出每个喷头的最远覆盖范围:
为什么是这样呢?看下图:
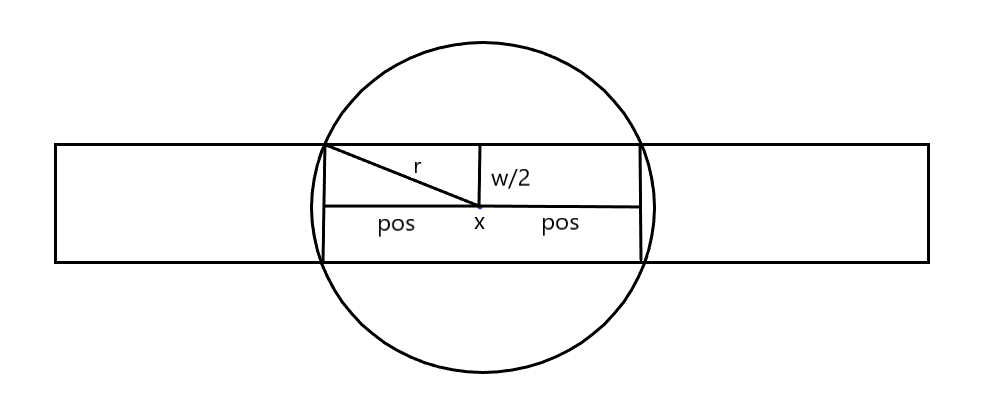
看上图,因为圆的边界并不好计算,所以可以把圆的覆盖范围近似的看做是上面的长方形。
那么根据勾股定理,很容易推导出上式,所以圆的覆盖范围就是:\([x-pos,x+pos]\)。
可能你会怀疑这样会不会掉精度而导致错误,答案是不会,而且还是唯一正确的方法。
因为在 \(x-pos\) 之前(或 \(x+pos\) 之后)的部分是没有完全覆盖的,倘若这段距离也加进去显然会导致错误。
然后就变成了和题目一一样的问题了,但是处理方法不尽相同:
- 将所有区间按照左端点(即 \(x-pos\))排序。
- 从左到右依次处理每个区间。(具体处理方法见代码)
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<iostream>
#include<cstring>
#define N 15010
using namespace std;
int T,n,L,W,cnt=0;
struct node{
double l,r;
}a[N];
int read(){
int x=0,f=1;char c=getchar();
while(c<'0' || c>'9') f=(c=='-')?-1:1,c=getchar();
while(c>='0' && c<='9') x=x*10+c-48,c=getchar();
return x*f;
}
void init(){
cnt=0;
n=read();L=read();W=read();
int x,r;
for(int i=1;i<=n;i++){
x=read();r=read();
if(r<=W/2) continue;
a[++cnt].l=(double)x-(double)sqrt(r*r-W*W/4.0);
a[cnt].r=(double)x+(double)sqrt(r*r-W*W/4.0);
}
return;
}
bool cmp(node a,node b){
return a.l<b.l;
}
void work(){
double t=0.0;
int ans=0,i=1;
while(t<L){
ans++;
double s=t;
for(;a[i].l<=s && i<=cnt;i++)
//核心代码:这个区间的左端点在上一次的右端点之前,并且没有超过区间总数时,进行叠加。
if(t<a[i].r) t=a[i].r;
//当这个区间的右端点在上一次选择的右端点之后时,可以抛弃上个区间而选择这个。(证明见例题一)
if(t==s && s<L){
//判断是否不可能,当并没有符合条件的区间,并且上一次的左端点<区间总长度,显然这是凉了。
printf("-1\n");return;
}
}
printf("%d\n",ans);
return;
}
int main(){
T=read();
while(T--){
init();
sort(a+1,a+cnt+1,cmp);
work();
}
}
第四题
很经典的问题啦,用标准的Johnson算法求解即可。
先给出做法,再给出证明吧。(读者可以自己尝试证明,其实也不难很难)
- 设 \(N_1\) 为 \(a<b\) 的作业集合,\(N_2\) 为 \(a\geq b\) 的作业集合。
- 将 \(N_1\) 集合按照 \(a\) 非减排序,\(N_2\) 集合按照 \(b\) 非增排序。
- 则答案为 \(N_1+N_2\) 集合。
时间复杂度为 \(O(N\ log\ N)\),证明如下:
设 \(S=\{J_1,J_2,...,J_N\}\),为待加工的作业排序,若 \(A\) 机器开始加工 \(S\) 时,\(B\) 还在加工其他零件,且加工时间为 \(t\)。
那么加工 \(S\) 的最短时间 \(T(S,t)=min_{1\leq i\leq N}\{a_i+T(S-\{J_i\}),b_i+max\{t-a_i,0\}\}\)。(自行理解)
假设最佳加工方案为先加工 \(J_i\) 再加工 \(J_j\),则有:
\(T(s,t)=a_i+T(S-\{J_i\},b_i+max\{t-a_i,0\})\)
\(=a_i+a_j+T(S-\{J_i,J_j\},b_j+max\{b_i+max\{t-a_i,0\}-a_j,0\})\)
\(=a_i+a_j+T(S(j_i,J_j),T_{ij})\)
\(T_{ij}=b_j+max\{b_i+max\{t-a_i,0\}-a_j,0\}\)
\(=b_i+b_j-a_j+max\{max\{t-a_i,0\}),a_j-b_i\}\)
\(=b_i+b_j-a_j+max\{t-a_i,a_j-b_i,0\}\)
\(=b_i+b_j-a_i-a_j+max\{t,a_i,a_i+a_j-b_i\}\)
\(case\ 1:=t+b_i+b_j-a_i-a_j(max\{t,a_i,a_i+a_j-b_i\}=t)\)
\(case\ 2:=b_i+b_j-a_i(max\{t,a_i,a_i+a_j-b_i\}=a_i)\)
\(case\ 3:=b_j(max\{t,a_i,a_i+a_j-b_i\}=a_i+a_j-b_i)\)
若按照作业 \(J_i\) 和作业 \(J_j\) 的加工顺序调换,则有:
\(T'(S,t)==a_i+a_j+T(S(j_i,J_j),T_{ji})\),其中
\(T_{ji}=b_i+b_j-a_i-a_j+max\{t,a_i,a_i+a_j-b_i\}\)
按假设,\(T\leq T'\),所以有:
\[max\{t,a_i+a_j-b_i,a_i\}\leq max\{t,a_i+a_j-b_j,a_j\} \]于是有:
\[a_i+a_j+max\{-b_i,-a_i\}\leq a_i+a_j+max\{-b_j,-a_i\} \]即:
\[min\{b_j,a_i\}\leq min\{b_i,a_j\} \]这就是上述算法的数学表达式形式。
证毕。
看完是不是眼花缭乱?所看几遍就好啦。
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<cstring>
#include<iostream>
#define N 1010
using namespace std;
int n,a[N],b[N],ans[N];
struct node{
int sum,num;
}c[N];
int read(){
int x=0,f=1;char c=getchar();
while(c<'0' || c>'9') f=(c=='-')?-1:1,c=getchar();
while(c>='0' && c<='9') x=x*10+c-48,c=getchar();
return x*f;
}
bool cmp(node a,node b){
return a.sum<=b.sum;
}
int main(){
n=read();
for(int i=1;i<=n;i++) a[i]=read();
for(int i=1;i<=n;i++) b[i]=read();
for(int i=1;i<=n;i++){
c[i].sum=min(a[i],b[i]);
c[i].num=i;
}
sort(c+1,c+n+1,cmp);
int l=0,r=n+1;
for(int i=1;i<=n;i++){
if(a[c[i].num]==c[i].sum) ans[++l]=c[i].num;
else ans[--r]=c[i].num;
}
int ans_a=0,ans_b=0;
for(int i=1;i<=n;i++){
ans_a+=a[ans[i]];
if(ans_b<ans_a) ans_b=ans_a;
ans_b+=b[ans[i]];
}//注意一下统计答案的方法,很简单的啦。
printf("%d\n",ans_b);
for(int i=1;i<n;i++) printf("%d ",ans[i]);
printf("%d\n",ans[n]);
return 0;
}
第五题
小学时市赛的最后一题(那时候我干了什么),用贪心 + 并查集解决,具体看这篇文章。
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<cstring>
#include<iostream>
#define N 510
using namespace std;
int M,n,fa[N];
struct node{
int t,c;
}a[N];
int read(){
int x=0,f=1;char c=getchar();
while(c<'0' || c>'9') f=(c=='-')?-1:1,c=getchar();
while(c>='0' && c<='9') x=x*10+c-48,c=getchar();
return x*f;
}
bool cmp(node a,node b){
if(a.c!=b.c) return a.c>b.c;
return a.t>b.t;
}
int find(int x){
if(fa[x]==x) return x;
return fa[x]=find(fa[x]);
}
int main(){
M=read();n=read();
for(int i=1;i<=n;i++) a[i].t=read();
for(int i=1;i<=n;i++) a[i].c=read();
for(int i=1;i<=n;i++) fa[i]=i;
sort(a+1,a+n+1,cmp);
int ans=0;
for(int i=1;i<=n;i++){
int f=find(a[i].t);
if(f<1) ans+=a[i].c;
else fa[f]=find(f-1);
}
printf("%d\n",max(0,M-ans));
return 0;
}
第六题
简单的贪心。
首先我们感性的理解一下,最大值与最小值一定是按照某种极端的顺序来得到的,于是想到从大到小与从小到大。
然后手玩样例发现最大值为从小到大,最小值为从大到小。于是有以下方法:
- 将数据从大到小排序,依次取出前两个数进行 \(a\times b+1\) 操作,并将结果压回队列。
- 建立小根堆,依次取出两次堆顶(前提是有至少两个数),进行 \(a\times b+1\) 操作,并将结果压回堆。
最后一个留在队列或堆中的数就是答案。
但是为什么一个只需要队列,一个却需要小根堆呢?
因为两个最大数进行 \(a\times b+1\) 操作一定还是最大数,但是两个最小数进行 \(a\times b+1\) 操作就不一定了。
举个栗子:10,9,8中9*8+1=73>10,而10*9+1一定>8。
至此本题已经做完了,但是贪心这个东西...仅仅靠感觉是很容易翻车的,所以要证明。证明如下:
使用反证法,这里仅进行 最大值为从小到大的证明,另一个同理即可。假设 \(a_1<a_2<...<a_n\) 。
按从小到大的顺序进行操作的答案为 \(ans1\),按 \(a_1,a_2,...,a_{i+1},a_i,...,a_n\) 进行操作的答案为 \(ans2\)。
假设 \(ans1<ans2\)。
则有:
\(((a_1\times a_2+1)\times...+1)\times a_n+1<((((a_1\times a_2+1)\times...+1)\times a_{i+1}+1)\times a_i+1)\times ...\times a_n+1\)
设:\(x=(a_{i-1}\times a_i+1)\times a_{i+1}+1,y=(a_{i-1}\times a_i+1)\times a_{i+1}+1\),将 \(x,y\) 带入两式。
发现其余部分都相同,得到 \(x<y\),即:(这里偷个懒,应该都能看懂吧)
\((a_{i-1}\times a_i+1)\times a_{i+1}+1<(a_{i-1}\times a_i+1)\times a_{i+1}+1\)
化简得:
\(a_{i+1}<a_i\)
与假设 \(a_1<a_2<...<a_n\) 相矛盾,所以假设不成立,所以 \(ans1\geq ans2\)。
并且可以拓展到普遍规律,得 \(ans1\) 为最佳答案。
证毕。
代码:
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<iostream>
#include<queue>
using namespace std;
int n,a[50010],mx,mn,jl=0;
priority_queue<int,vector<int>,greater<int> >q;
int read(){
int x=0,f=1;char c=getchar();
while(c<'0' || c>'9') f=(c=='-')?-1:1,c=getchar();
while(c>='0' && c<='9') x=x*10+c-48,c=getchar();
return x*f;
}
bool cmp(int a,int b){
return a>b;
}
int main(){
n=read();
for(int i=1;i<=n;i++){
a[i]=read();
q.push(a[i]);
}
a[0]=read();
sort(a+1,a+n+1,cmp);
mn=a[1];
for(int i=2;i<=n;i++) mn=mn*a[i]+1;
while(!q.empty()){
mx=q.top();q.pop();
if(!q.empty()) mx=mx*q.top()+1;q.pop();//if 判断不可少
if(!q.empty())q.push(mx);//if 判断不可少
}
printf("%d\n",mx-mn);
return 0;
}
第七题
一开始看错了题,还以为是什么二分答案 + 贪心。
题目要求的是连续若干段,所以数字不能像背包里装物品一样多以切换背包,例如:
4 6
2 3 6 1
这组数据的答案就是 3 而不是 2。(如果你没有看错题甚至认为我很好笑,请勿喷)
然后就是常规操作了,贪心的使每一段尽量长就好了。
证明略...(实在太简单啦)
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<iostream>
using namespace std;
int n,m,a[100010],ans=0,sum=0;
int read(){
int x=0,f=1;char c=getchar();
while(c<'0' || c>'9') f=(c=='-')?-1:1,c=getchar();
while(c>='0' && c<='9') x=x*10+c-48,c=getchar();
return x*f;
}
int main(){
n=read();m=read();
for(int i=1;i<=n;i++) a[i]=read();
for(int i=1;i<=n;i++){
if(sum+a[i]<=m) sum+=a[i];
else{ans++;sum=a[i];}
}
if(sum) ans++;
printf("%d\n",ans);
return 0;
}
第八题
和第一题的代码一模一样,但是要将数组范围调大一点。忍不住说一句:一本通的习题这么水的吗
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<iostream>
#include<cstring>
#define N 1000010
using namespace std;
int n;
struct node{
int s,f;
}a[N];
int read(){
int x=0,f=1;char c=getchar();
while(c<'0' || c>'9') f=(c=='-')?-1:1,c=getchar();
while(c>='0' && c<='9') x=x*10+c-48,c=getchar();
return x*f;
}
bool cmp(node a,node b){
return a.f<b.f;
}
int main(){
n=read();
for(int i=1;i<=n;i++){
a[i].s=read();a[i].f=read();
}
sort(a+1,a+n+1,cmp);
int ans=1,jl=a[1].f;
for(int i=2;i<=n;i++){
if(a[i].s>=jl){
ans++;jl=a[i].f;
}
}
printf("%d\n",ans);
return 0;
}
第九题
和第五题一样?这本书...[无语.jpg]
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<cstring>
#include<iostream>
#define N 1000010
using namespace std;
int M,n,fa[N];
struct node{
int t,c;
}a[N];
int read(){
int x=0,f=1;char c=getchar();
while(c<'0' || c>'9') f=(c=='-')?-1:1,c=getchar();
while(c>='0' && c<='9') x=x*10+c-48,c=getchar();
return x*f;
}
bool cmp(node a,node b){
if(a.c!=b.c) return a.c>b.c;
return a.t<b.t;
}
int find(int x){
if(fa[x]==x) return x;
return fa[x]=find(fa[x]);
}
int main(){
n=read();
for(int i=1;i<=n;i++){
a[i].t=read();a[i].c=read();
}
for(int i=1;i<=n;i++) fa[i]=i;
sort(a+1,a+n+1,cmp);
int ans=0;
for(int i=1;i<=n;i++){
int f=find(a[i].t);
if(f<1) continue;
ans+=a[i].c;
fa[f]=find(f-1);
}
printf("%d\n",ans);
return 0;
}
第十题
真是一道好题呀,一开始想的是用 DP 来做,过了之后去康了康 dalao 的题解才发现了巧妙的贪心做法。
先是 DP 吧,用 \(f[i,j]\) 表示第 \(i\) 个池塘,共用 \(j\) 个时间钓鱼。(注意,仅仅是钓鱼时间)
则有状态转移方程:\(f[i,j]=max_{0\leq k\leq j}\{f[i-1,j-k]+\sum_{l=0}^{k-1} a_i-(b_i\times l) \}\)
时间复杂度为:\(O(nh^3)\)。
代码:
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <iostream>
#include <cstring>
#define N 2010
using namespace std;
int n, h, a[N], b[N], t[N], tt, f[N][N], ans = 0;
int read() {
int x = 0, f = 1;
char c = getchar();
while (c < '0' || c > '9') f = (c == '-') ? -1 : 1, c = getchar();
while (c >= '0' && c <= '9') x = x * 10 + c - 48, c = getchar();
return x * f;
}
int main() {
n = read();
h = read();
h *= 12;
for (int i = 1; i <= n; i++) a[i] = read();
for (int i = 1; i <= n; i++) b[i] = read();
for (int i = 2; i <= n; i++) {
tt = read();
t[i] = t[i - 1] + tt;
}
memset(f, 0, sizeof(f));
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= h - t[i]; j++) {
f[i][j] = f[i][j - 1];
for (int k = 0; k <= j; k++) {
if (a[i] < (k - 1) * b[i])
break;
int s = 0;
for (int l = 0; l < k; l++) s += a[i] - (b[i] * l);
f[i][j] = max(f[i][j], f[i - 1][j - k] + s);
}
ans = max(ans, f[i][j]);
}
}
printf("%d\n", ans);
return 0;
}
然后是贪心。
题目中说了某些湖,我们就要枚举每一个湖作为结束点,然后用 总时间-走路的时间=能钓鱼的次数,记为 \(sum\)。
如样例:
第一个湖:4 3 2 1 0 0 0…
第二个湖:5 3 1 0 0 0…
第三个湖:6 5 4 3 2 1 0 0 0…
此题就是让我们从中选择 \(sum\) 个最大的数。
我们在第 \(i\) 个湖中选了 \(x\) 个数,在 \(j\) 个湖中选了 \(y\) 个数,就相当于我们在第 \(i\) 个湖中钓了 \(x\) 次鱼,在第j个湖中钓了 \(y\) 次鱼了。
因为 \(d[i]\geq 0\),所以所有数列呈递减排序,于是如果我们要选择某一个数列的第 \(i\) 个数,这个数列的前 \(i-1\) 个数都已
经被选了(因为比第 \(i\) 个数大),所以是符合题意的。
代码如下,用优先队列优化,时间最坏为 \(O(n\ log(nh))\):(证明过于简单,略过)
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <iostream>
#include <cstring>
#include <queue>
#define N 2010
using namespace std;
int n, h, a[N], b[N], t[N], ans = 0;
struct node {
int sum, cha;
bool operator<(const node &a) const { return a.sum > sum; }
};
priority_queue<node> q;
int read() {
int x = 0, f = 1;
char c = getchar();
while (c < '0' || c > '9') f = (c == '-') ? -1 : 1, c = getchar();
while (c >= '0' && c <= '9') x = x * 10 + c - 48, c = getchar();
return x * f;
}
int main() {
n = read();
h = read();
h *= 12;
for (int i = 1; i <= n; i++) a[i] = read();
for (int i = 1; i <= n; i++) b[i] = read();
for (int i = 1; i < n; i++) t[i] = read();
int Sum = 0, sum = 0, m;
for (int i = 1; i <= n; i++) {
sum = 0;
Sum += t[i - 1];
m = h - Sum;
node p;
for (int j = 1; j <= i; j++) {
p.sum = a[j];
p.cha = b[j];
q.push(p);
}
while (m > 0 && !q.empty() && q.top().sum > 0) {
sum += q.top().sum;
p.sum = q.top().sum - q.top().cha;
p.cha = q.top().cha;
q.pop();
q.push(p);
m--;
}
ans = max(ans, sum);
}
printf("%d\n", ans);
return 0;
}
第十一题
环形均分纸牌问题。
一般的均分纸牌问题就相当于在第N个人与第1个人之间把环断开,此时这N个人站成一行,其持有的纸牌数、前缀和分别是:
A[1] S[1]
A[2] S[2]
…
A[N] S[N]
如果在第K个人之后把环断开站成一行,这N个人持有的纸牌数、前缀和分别是:
A[k+1] S[k+1]-S[k]
A[k+1] S[k+2]-S[k]
…
A[N] S[N]-S[k]
A[1] S[1]+S[N]-S[k]
…
A[k] S[k]+S[N]-S[k]
所以,所需最小花费为:\(\sum_{i=1}^{N}|S[i]-S[k]|\)。
当K取何值时上式最小?这就是“货仓选址”问题。
所以我们将 \(S\) 数组从小到大排序,取中位数作为 \(S[k]\) 就是最优解。
#include<cstdio>
#include<algorithm>
#include<iostream>
#define N 1000010
using namespace std;
typedef long long ll;
ll n,a[N],sum[N],ave=0,ans=0;
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%lld",&a[i]);ave+=a[i];
}
ave/=n;
for(int i=1;i<=n;i++) a[i]-=ave;
for(int i=1;i<=n;i++) sum[i]=sum[i-1]+a[i];
sort(sum+1,sum+n+1);
ll mid=sum[(n+1)>>1];
for(int i=1;i<=n;i++) ans+=abs(mid-sum[i]);
printf("%lld\n",ans);
return 0;
}