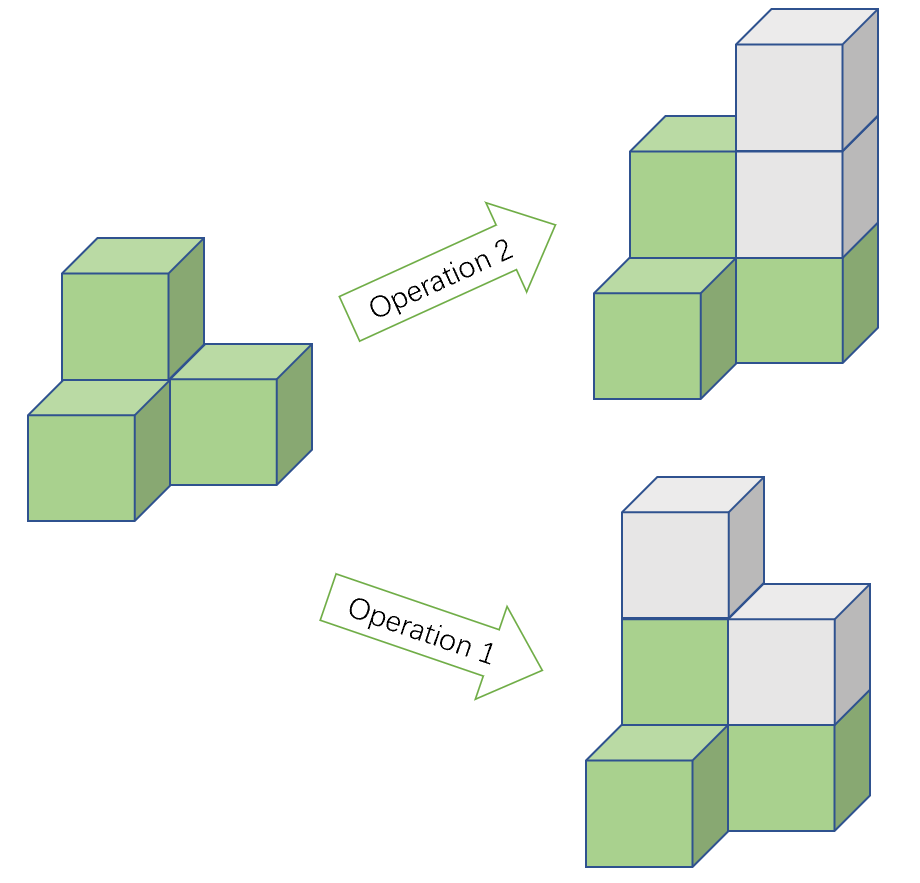
分析:
1.每个方格中立方体的数量不重要,重要的是数量的奇偶性。
因为操作2可以把相同奇偶性的方格中的立方体数量变为一致,不同奇偶性的也可以变为相同的奇偶性。
2.可以在同时改变两个方格 \(u,v\) 数量的奇偶性,不管是否是相邻。
因为,两个方格之间必然存在一条路径:\(w_0w_1w_2...w_n\),其中 \(w_0=u,w_n=v\)。对该条路径进行操作 \(1\),就可以保证除路径的起点和端点数量增加 \(1\),奇偶性改变外,路径上其余点的数量都增加 \(2\),奇偶性不变。
3.当 \(n\times m\) 为奇数时,无论初始状态如何,最终都可以转换为目标状态。
因为一个奇数必然等于一个奇数加上一个偶数,所以必然存在 偶数个方格数量为奇数个 或者 偶数个方格数量为偶数,这两种情况中的一种。根据 \(2\) 的结论,可以改变着偶数个方格的奇偶性,再利用操作 \(2\),就可以达到目的。
4.当 \(n\times m\) 为偶数,并且 \(\sum_{i=1}^{n}{\sum_{j=1}^{m}{a_{i,j}}}\) 为偶数时,无论初态如何,最终都可以转化为目标状态。
因为偶数等于两个奇数或者两个偶数之和,如果数量为偶数和数量为奇数的方格数均为偶数,分析和 \(3\) 相同。而且不存在二者均为奇数的情况,否则 \(sum\) 就不满足条件。
5.当 \(n\times m\) 为偶数,并且 \(\sum_{i=1}^{n}{\sum_{j=1}^{m}{a_{i,j}}}\) 为奇数时,无论初态如何,采用怎样的策略,最终都不可能转化为目标状态。
实现:
当 \(n\times m\) 为奇数时,\(ans=(R-L+1)^{nm}\ \%mod\);
当 \(n\times m\) 为偶数时,
令 \([L,R]\) 内的奇数个数为:\(x\),偶数个数为 \(y\);
那么
\[ans=\sum_{i=0}^{\frac{nm}{2}} {C_{nm}^{2i} * x^{2i} * y^{nm-2i}} \]
二项式展开(把 \(y\) 的幂按奇和偶分开):
\[(x+y)^{n}=\sum_{i=0}^{n/2}{C_{n}^{2i}x^{2i}y^{n-2i}}+\sum_{i=1}^{n/2}{C_{n}^{2*i-1}x^{2i-1}y^{n-2i+1}} \]
\[(x-y)^{n}=\sum_{i=0}^{n/2}{C_{n}^{2i}x^{2i}y^{n-2i}}-\sum_{i=1}^{n/2}{C_{n}^{2*i-1}x^{2i-1}y^{n-2i+1}} \]
两式相加,再除 \(2\),即可得到所求答案。
代码 \(1\)
\(C++)\):
#include <bits/stdc++.h>
using namespace std;
const int mod=998244353;
const int inv=499122177;
typedef long long ll;
ll power(ll a,ll b)
{
ll res=1;
a%=mod;
while(b)
{
if(b&1)
res=res*a%mod;
a=a*a%mod;
b>>=1;
}
return res%mod;
}
int main()
{
ll n,m,L,R;
scanf("%lld%lld%lld%lld",&n,&m,&L,&R);
if((n*m)&1)
printf("%lld\n",power(R-L+1,n*m));
else
{
ll x=(R-L+1)/2;
ll y=(R-L+1)-x;
printf("%lld\n",(power(x+y,n*m)+power(x-y,n*m))%mod*inv%mod);
}
return 0;
}
\(python\):
mod=998244353
n,m,L,R=map(int,input().split())
if (n*m)%2==1:
print(pow(R-L+1,n*m,mod))
else:
x=int((R-L+1)/2)
y=(R-L+1)-x
print((pow((x+y),n*m,mod)+pow((x-y),n*m,mod))%mod*pow(2,mod-2,mod)%mod)