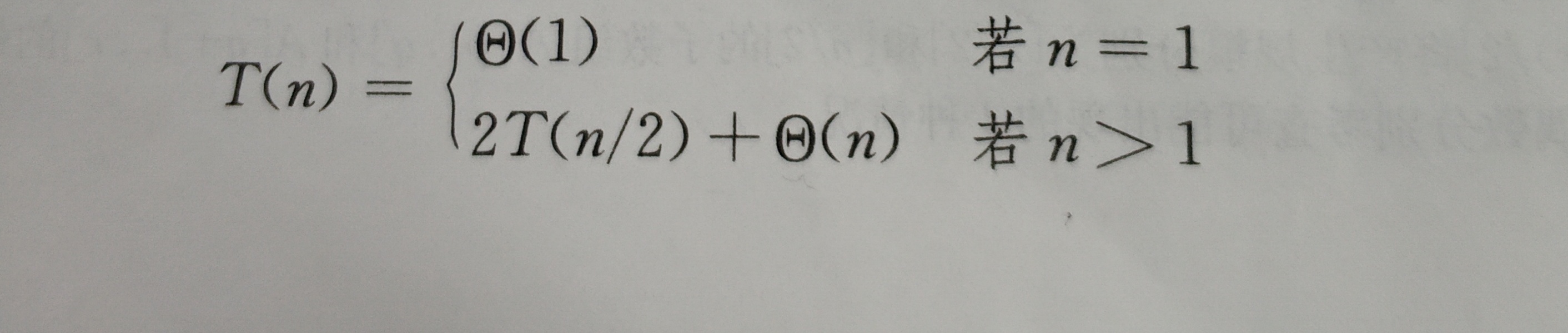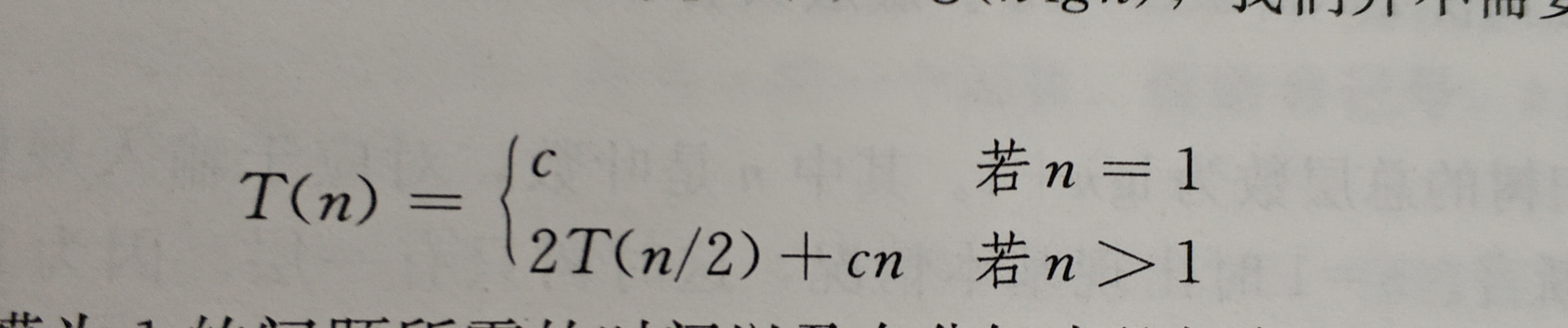先简单的了解一下分治法的主要思想:
主要分为三个步骤
1.分解:将原问题分解成若干个子问题,这些子问题是原问题的规模较小的实例;
2.解决:解决这些子问题,递归的求解各个子问题,然而,若子问题规模足够小,则直接求解;
3.合并:将这些子问题的解成原问题的解。
下面我们先实现一个辅助过程Merge(A,p,q,r),该函数有四个参数,其中A为一个序列(数组),p,q,r为A的下标值;
该过程中假设子数组A[p....q]和A[p+1...r]都已经排好序。Merge的功能就是将这两个子数组合并成一个新的数组(以排序)
下面是Merge函数的伪代码:
n1=q-p+1; //设置两个子数组大小;
n2=r-q;
Let L[1...n1+1]and R[1...n2+1] be new array;//定义两个子数组,并将子数组最后一个值设为“哨兵值”主要是为了方便判断
for i=1 to n1 //将L[i]数组赋值,填充吧。
L[i]=A[p+i-1];
for j=1 to n2 //将数组R赋值;
R[j]=A[q+j];
L[n1+1]=∞; //将两个子数组的最后一位设置为无穷大;
R[n2+1]=∞;
i=1; //设置初始比较的值
j=1;
for k=p to r //循环将数组A重新排序
if L[i]<=R[j] //如果当前比较值中L[i]小
A[k]=L[i]; //则将L中的当前值赋值给A;
i=i+1 //然后L下标加一,让L中的下一位元素继续比较
else
A[k]=R[j];
j=j+1;
下面我们将Merge看做是一个子程序,现在我们定义函数Merge-Sort(A,p,r)
伪代码如下:
Merge-Sort(A,p,r):
if(p<r)
q=(p+r)/2
Merge-Sort(A,p,q);
Merge-Sort(A,q+1,r);
Merge(A,p,q,r);
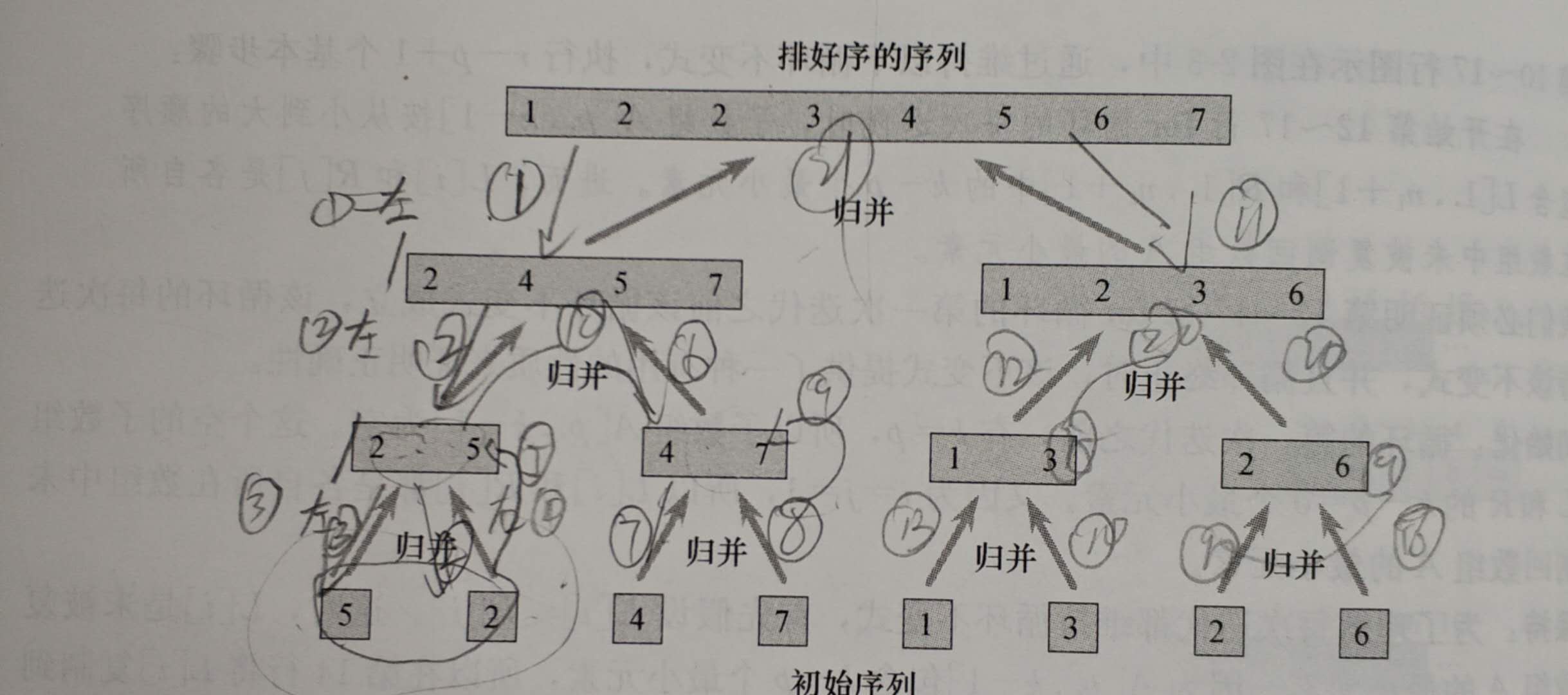
下面是一幅图形象的描述了并归排序的步骤
我们来分析它的时间复杂度:
当规模较小时,我们直接求解,所以我们需要常量时间。
假设我们把原问题分解成a个子问题时:每个子问题的规模是原问题的1/b,(这里a,b都为2),为了求解一个规模为n/b的子问题,我们需要T(n/b),a个这样的子问题,则所需时间为aT(n/b),假设我们分解的时间需要C(n),合并的时间需要D(n);
综上可得到如下表达式:
在分析:
分解步骤我们仅仅只需要只要中间值,需要常量时间,
解决两个规模为N/2的子问题,我们需要2T(n/2);
合并过程我们可以分析Merge过程易知为:O(n);
所以将D(n)、C(n)相加还是为O(n)
最终T(n)的递归式如下:
最后来分析T(n)具体为多少:
我们先把递归式重写如下:
下面我们用递归树详细描述:
一共有lgn +1层,每层的代价都是cn所以:
最后我们我们得出:T(n)=cn *(lgn +1)=cn* lgn +cn