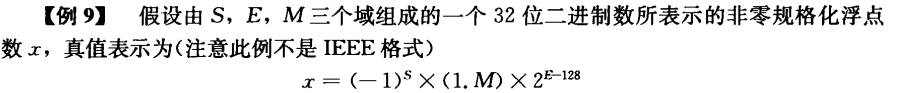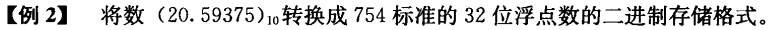本章首先讲述计算机中数据与文字的表示方法,然后讲述定点运算,定点运算器的组成,最后讲述浮点运算方法,浮点运算器的组成。
范围问题
纯小数范围:
0≤∣x∣≤1−2n
纯整数范围:
0≤∣x∣≤2n−1

定点整数的补码:
−2n≤[x]移≤2n−1

定点小数的补码:
−1≤[x]移≤1−2−n
例如
当n为4时:
真值:-1111~+1111
补码:10001~01111(注意正数的补码不变)
⇒ 10000~01111
⇒-16 ~15
原码的定点整数:
[x]原={x,2n−x=2n+∣x∣,2n ⩾ x ⩾0 0 ⩾ x ⩾ −2n
例如:
x=+1001,则
[x]原=01001
x=−1001,则
[x]原=11001
补码的表示方法
这里有一个有趣的说法:
我们可以把补码视作一个无头无尾的圆,可以正向走,可以反向走。
−3=+9(mod)12
如何来理解这样的式子呢?
我们将其普遍化,令前一个数的绝对值为
x,第二个数的绝对值为
y,第三个数为
z;我们发现第一个数的绝对值与第二个数的绝对值之和为第三个数,即
x+y=z;列方程为:
(z−a)mod(z)=[z+(z−a)]mod(z)
正负补码与真值的关系

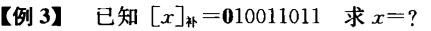
x=0×28+1×27+0×26+0×25+1×24+1×23+0×22+1×21+1×20
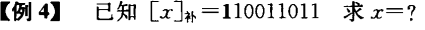
x=−1×28+1×27+…+1×20
补码表示法的创新点:
- 用加法代替减法
[a]补−[b]补=[a]补+[−b]补
[b]补→[−b]补⇒连同符号位取反加一
- 0只有一种表示方法
移码的表示法
[e]移=2k+e
当
x=+10101时,
[x]移=25+x=100000+10101=1,10101
移码是补码符号位取反
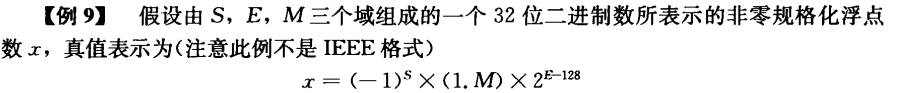
最大正数
01111111111111111111111111111111
x=[1+(1−223)]×2255−128
最小正数:
00000000000000000000000000000000
x=1×2−128
最小负数:
11111111111111111111111111111111
x=−[1+(1−223)]×2127
最大负数:
10000000000000000000000000000000
x=−1×2−128
归纳范围问题
IEEEE754浮点数的表示范围:


规格化问题
在IEEEE754标准中,一个规格化的32位浮点数
x 的真值表示为:
x=(−1)S×2E−127×(1.M)
e=E−127
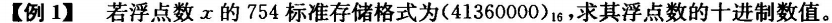
将16进制展开:
0S
10000010阶码(8位)
01101100000000000000000尾数(23位)
阶码:
e=E−127 =3
尾数:
1.M=1.01101100000000000000000=1.011011
x=(−1)0×(1.011011)×23
x=1011.011=(11.375)10
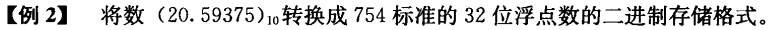
将10进制换成2进制,方法同上

这里的位数我所理解的是:因为一个十进制所要占用半个字节,也就是4位二进制,所以十进制的位数一定要占满完整的字节,也就是说十进制位数要为偶数。
上面的两个例题都是将二进制转化为IEEEE754格式的浮点数(在审题时要读清楚)
奇校验和偶校验
注意两点要求:
- 最后一位为校验位:偶校验:前面数为1的个数为偶数校验位为0,反之亦然;奇校验:前面数为1的个数为奇数校验位为0
- 包括校验位,当为1的数为奇数时,传输信息有误,反之亦然。
定点加法减法运算
补码加法

符号位要参与运算;在模
2n+1意义下相加,即超过
2n+1要丢掉
补码减法
上面已有提到,不再叙述。
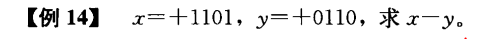
[x]补=01101[y]补=00110
[−y]补=11010
x−y=[x−y]补=[x]补−[y]补=[x]补+[−y]补=01101+11010=(1)00111
故:
x−y=+0111
判断是否溢出
第一种:双符号位:
[x]变形补码=2n+2+x
- 正数直接在前面加两个0
- 负数用
2n+2−∣x∣
- 如果符号位位01则为正溢出,10则为负溢出
第二种:

定点乘法运算

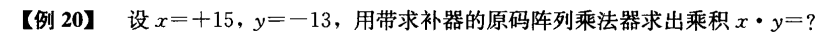
∣x∣=1111,∣y∣=1101


[x]补=10001,[y]补=10011
尾数部分算前求补器输出为:
∣x∣=1111,∣y∣=1101
说明:从右到左数到第一个1时,该位置左边全部取反,该位置右边包括该数全部不变

最后单独加上符号位