【Machine Learning】梯度下降算法介绍_02

前言

此篇文章大体介绍了一下关于梯度下降算法的一些基本概念性知识，接下来我们继续更深层次的来了解一下梯度下降算法。

一、梯度

       梯度的本意是一个向量(矢量)，表示一个函数在该点出的方向导数的取得的最大值，或者说函数在该点出沿着该方法(此梯度的方向也就是求导的方向)变化率最大、最快；亦是在微积分里面，对多元函数参数求偏导，把求的各参数的偏导数以向量形式写出来，就是梯度。
       从几何意义上讲，梯度向量就是函数变化最快的地方，沿着梯度方向就能得到函数的最大值，相反的话就能获取梯度下降的最小值。
       梯度下降和梯度上升是可以互相转化。求损失函数 $f(θ)$的最小值，用梯度下降法迭代；亦可反过来求损失函数 $-f(θ)$的最大值，用梯度上升法。
       【百度百科】梯度下降是迭代法的一种,可以用于求解最小二乘问题(线性和非线性都可以)。在求解机器学习算法的模型参数，即无约束优化问题时，梯度下降（Gradient Descent）是最常采用的方法之一，另一种常用的方法是最小二乘法。在求解损失函数的最小值时，可以通过梯度下降法来一步步的迭代求解，得到最小化的损失函数和模型参数值。反过来，如果我们需要求解损失函数的最大值，这时就需要用梯度上升法来迭代了。在机器学习中，基于基本的梯度下降法发展了两种梯度下降方法，分别为随机梯度下降法和批量梯度下降法

---

       梯度是一个向量，表示某一函数在该点处的方向导数 ，沿着该方向取最大值，即函数在该点处沿着该方向变化最快，变化率最大（即该梯度向量的模）；当函数为一维函数的时候，梯度就是导数。

1.1 导数

提到导数，相比大家都应该不陌生吧，它代表的含义就是反应出曲线变化快慢。
一阶导数：就是曲线的斜率，是曲线变化快慢的一个反应
二阶导数：是斜率变化的反应，表现曲线的凹凸性
$\begin{array}{c}{y=f(x)} \\ {y^{\prime}=f^{\prime}(x)=\frac{d y}{d x}=\lim _{\Delta x \rightarrow 0} \frac{\Delta y}{\Delta x}=\lim _{\Delta x \rightarrow 0} \frac{f\left(x_{0}+\Delta x\right)-f\left(x_{0}\right)}{\Delta x}}\end{array}$

高等数学中专门有关于导数的学习

1.2 偏导数

       导数是针对单一变量的，当函数是多变量的，偏导数就是关于其中一个变量的导数而保持其他变量恒定不变（固定一个变量求导数）。
       假定一个二元函数点 $z=f(x,y)$，点 $(x_0,y_0)$是其定义域内的一个点，将 $y$固定在 $y_0$上，而 $x$在 $x_0$上增量 $\Delta x$,相应的函数 $z$有增量 $\Delta z=f\left(x_{0}+\Delta x, y_{0}\right)-f\left(x_{0}, y_{0}\right)$; $\Delta z$和 $\Delta x$的比值当 $\Delta x$的值趋向于0的时候，如果极限存在，那么此极限称为函数 $z=f(x, y)$在点 $(x_0,y_0)$处对 $x$的偏导数，记作： $f_{x}^{\prime}\left(x_{0}, y_{0}\right)$

对 $x$的偏导数：

$\frac{\partial f}{\partial x} |\left(x=x_{0}, y=y_{0}\right)$

对 $y$的偏导数：

$\frac{\partial f}{\partial y} |\left(x=x_{0}, y=y_{0}\right)$

---

二、举例梯度下降

举例解释梯度下降
比如我们在山上的某处，我们不知道如何下山，于是就决定走一步算一步(船到桥头自然直思想)。

1、也就是每走到一个位置的时候，计算当前位置的梯度，沿着梯度的负方向，也就是当前最陡峭的位置向下走一步
2、继续求解当前位置梯度，向这一步所在位置沿着最陡峭易下山的位置走一步。
3、如此一步步的走下去，一直走到我们自己认为到了山脚。(有可能这样一直走下去到不了山脚，而是到了某一个局部的山峰低处)。

也就是说，梯度下降并不一定能get到全局的最优解，有时候可能获取到局部最优解。当然，如果损失函数是凸函数，梯度下降得到的解就一定是全局最优解。
借图如下所示：

---

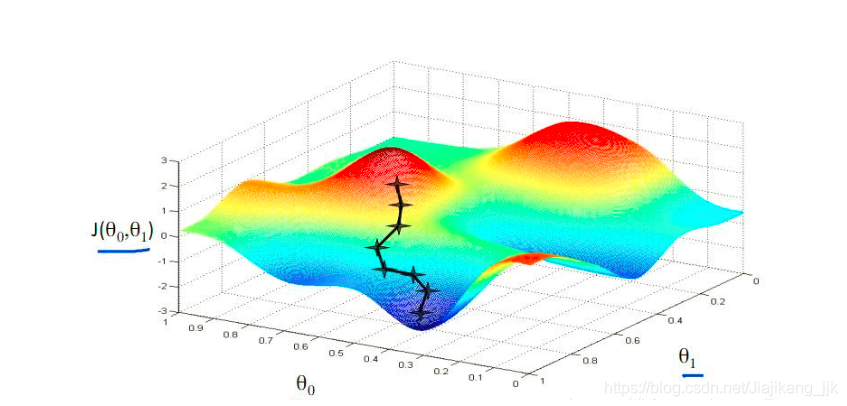
梯度下降法常用于求解无约束情况下凸函数的极小值，是一种迭代类型的算法，因为凸函数只有一个极值点，故求解出来的极小值就是函数的最小值点。

$\begin{array}{c}{J(\theta)=\frac{1}{2 m} \sum_{i=1}^{m}\left(h \theta\left(x^{(i)}\right)-y^{(i)}\right)^{2}} \\ {\theta^{*}=\arg \min _{\theta} J(\theta)}\end{array}$
梯度下降优化思想

用当前位置的负梯度方向作为搜索方向，因为该方向为当前位置下降最快的方向，所以梯度下降法也被称为“最速下降法”。梯度下降法中越接近目标值，变化量越小。

计算公式如下（迭代公式）：
$\theta^{k+1}=\theta^{k}-\alpha \Delta f\left(\theta^{k}\right)$

α被称为步长或者学习率，表示自变量 x每次迭代变化的大小
收敛条件：当目标函数的函数值变化非常小的时候或者达到最大迭代次数的时候，就结束循环。

三、训练样本

我们从 $1—>n$的方式扩展训练样本，以此，来观察训练样本的变化。
求解使得 $J(\theta)$最小时， $\theta$值的基本思想：

1：首先随便给 $\theta$一个初始值
2：然后改变 $\theta$ 值让 $J(\theta)$的取值变小
3：不断重复 $\theta$使得 $J(\theta)$变小的过程直至 $J(\theta)$达到最小值

步骤

• 目标函数 $\theta$求解：
  $J(\theta)=\frac{1}{2} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}-y^{(i)}\right)^{2}\right.$

• 初始化 $\theta$(随机初始化，可以初始化为0滴)

• 沿着负梯度方向迭代，更新后的 $\theta$使得 $J(\theta)$更小：

  $\theta_{j}=\theta_{j}-\alpha \frac{\partial J(\theta)}{\partial \theta_{j}}$

      其中， $\alpha$是学习率、步长；它控制 $\theta$每次向 $J(\theta)$变小的方向迭代时的变化幅度。 $J(\theta)$对 $\theta$偏导表示 $J(\theta)$变化最大的方向。由于求的是极小值，因此梯度方向是偏导数的反方向。

---

求解偏导：
$\frac{\partial}{\partial \theta_{j}} J(\theta)=\frac{\partial}{\partial \theta_{j}} \frac{1}{2}\left(h_{\theta}(x)-y\right)^{2}$

$\begin{array}{c}{=2 * \frac{1}{2}\left(h_{\theta}(x)-y\right) * \frac{\partial}{\partial \theta_{j}}\left(h_{\theta}(x)-y\right)} \\ {=\left(h_{\theta}(x)-y\right) * \frac{\partial}{\partial \theta_{j}}\left(\sum_{i=0}^{n} \theta_{i} x_{j}-y\right)} \\ {=\left(h_{\theta}(x)-y\right) x_{j}}\end{array}$

其中： $h_{\theta}(x)=\sum_{i=0}^{n} \theta_{i} x_{j}$；那么 $\theta$的迭代公式就是：
$\theta_{j}=\theta_{j}+\alpha\left(y-h_{\theta}(x)\right) x_{j}$

四、梯度下降

4.1 量梯度下降(Batch Gradient Descent,BGD)

批量梯度下降法，是梯度下降法最常用的形式，具体做法也就是在更新参数时使用所有的样本来进行更新。

• 处理一个样本公式： $\theta_j = \theta_j + \alpha(y-h_\theta(x))x_j$
• 处理多个样本公式：
  $\begin{array}{c}{\frac{\partial}{\partial \theta_{j}} J(\theta)=\sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) x_{j}^{(i)}} \\ {\theta_{j}=\theta_{j}+\alpha \sum_{i=1}^{m}\left(y^{(i)}-h_{\theta}\left(x^{(i)}\right)\right) x_{j}^{(i)}}\end{array}$

每一步都是计算全部训练集的数据，所以称之为批量梯度下降。由于每次迭代的时候都要对所有的数据集计算求和，计算量就会特别的大，尤其是训练数据集特别大的时候。此外，我们就可用随机梯度下降。

4.2 随机梯度下降（Stochastic Batch Gradient Descent，SGD)

      随机梯度下降在计算下降最快的方向时，随机选一个数据进行计算，而不是扫描全部训练数据集，这样就加快了迭代速度。
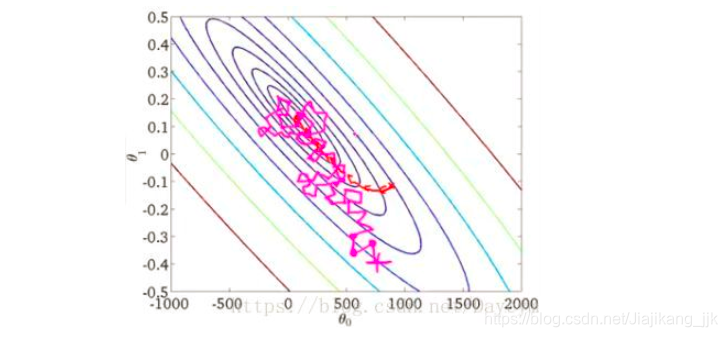
SGD下降并不是沿着 $J(\theta)$下降最快的方法收敛，而是震荡的方式趋向极小点。
借图如下所示：

迭代公式：

Loop{

for i = 1 to m {

$\theta_{j} :=w_{j}+\alpha\left(y_{i}-\theta_{i}^{T} x_{i}\right) x_{j}$
}
}

4.3 BGD和SGD算法比较

1、BGD速度比SGD速度慢(迭代次数多)
2、SGD在某些情况下(全局存在多个相对最优解),SGD有可能跳出某些小的局部最优解，所以不会比BGD坏。
3、BGD一定能够得到一个局部最优解(在线性回归模型中一定是得到一个全局最优解)，SGD由于随机性的存在可能导致最终结果比BGD的差。

4.3 小批梯度下降(Mini Batch Gradient Descent,MBGD)

      如果既要保证算法的训练过程比较快，又需要保证最终参数训练的准确率，可以选择小批梯度下降。MBGD中不是每拿一个样本就更新一次梯度，而是拿 $b$个样本( $b$一般为10)的平均梯度作为更新方向。
迭代公式：

Repeat{

for i = 1, 11, 21,31,…m{

$\theta_{j} :=\theta_{j}+\alpha \frac{1}{10} \sum_{i}^{i+9}\left(y_{i}-\theta_{i}^{T} x_{i}\right) x_{j}$

}

}

到了这里，基本算是对于BGD、SGD、MBGD有了基本的了解了，那接下来咋们就简单实际操作一丢丢。

五、梯度下降的简单实现

5.1 批量梯度下降(BGD)

"""
 author:jjk
 datetime:2019/8/19
 coding:utf-8
 project name:Pycharm_workstation
 Program function:
 
"""

import numpy as np
# 构造训练数据集
x_train = np.array([[2, 0., 3], [3, 1., 3], [0, 2., 3], [4, 3., 2], [1, 4., 4]])
m = len(x_train)
x0 = np.full((m,1),1)
# 构造一个每个数据第一维特征都是1的矩阵
input_data = np.hstack([x0,x_train])
m,n = input_data.shape
theta1 = np.array([[2,3,4]]).T
# 构建标签数据集，后面的np.random.randn是将数据加一点噪声，仪表模拟数据集
#y_train = (input_data.dot(np.array([1, 2, 3, 4]).T)).T
y_train = x_train.dot(theta1) + np.array([[2],[2],[2],[2],[2]])

# 设置两个终止条件
loop_max = 1000000
epsilon = 1e-5
# 初始theta
np.random.seed(0) # 设置随机种子
theta = np.random.randn(n,1) # 随机去一个1维列向量初始化theta

# 初始化步长/学习率
alpha = 0.00001
# 初始化误差，每个维度的theta都应该有一个误差，所以误差是4维
error = np.zeros((n,1)) # 列向量

# 初始化偏导数
diff = np.zeros((input_data.shape[1],1))
# 初始化循环次数
count = 0

while count < loop_max:
    count += 1
    sum_m = np.zeros((n,1))
    for i in range(m):
        for j in range(input_data.shape[1]):
            diff[j] = (input_data[i].dot(theta)-y_train[i])*input_data[i,j]
        # 求每个维度的梯度的累加和
        sum_m = sum_m + diff
    # 利用这个累加和更新梯度
    theta = theta - alpha*sum_m
    # else中将前一个theta赋值给error，theta-error便表示前后两个梯度的变化，当梯度变化小(在接收的范围内)时，便停止迭代

    if np.linalg.norm(theta-error) < epsilon:
        break
    else:
        error = theta
print(theta) # 输出梯度：真实的应该是2234

源码获取：此链接下的BGD.py文件

---

5.2 随机梯度下降(SGD)

"""
 author:jjk
 datetime:2019/9/21
 coding:utf-8
 project name:Pycharm_workstation
 Program function:
 
"""

import numpy as np
# 构造训练数据集
x_train = np.array([[2, 0., 3], [3, 1., 3], [0, 2., 3], [4, 3., 2], [1, 4., 4]])
# 构建一个权重作为数据集的真正的权重，theta1主要是用来构建y_train，然后通过模型计算
# 拟合的theta，这样可以比较两者之间的差异，验证模型。
theta1 = np.array([[2,3,4]]).T

# 构建标签数据集,y=t1*x1+t2*x2+t3*x3+b即y=向量x_train乘向量theta+b, 这里b=2
y_train = (x_train.dot(theta1) + np.array([[2],[2],[2],[2],[2]])).ravel()

# 构建一个5行1列的单位矩阵x0，然它和x_train组合，形成[x0, x1, x2, x3]，x0=1的数据形式，
# 这样可以将y=t1*x1+t2*x2+t3*x3+b写为y=b*x0+t1*x1+t2*x2+t3*x3即y=向量x_train乘向
# 量theta其中theta应该为[b, *, * , *]，则要拟合的theta应该是[2,2,3,4]，这个值可以
# 和算出来的theta相比较，看模型的是否达到预期

x0 = np.ones((5,1))
input_data = np.hstack([x0,x_train])
m,n = input_data.shape

# 设置两个终止条件
loop_max = 10000000
epsilon = 1e-6
# 初始化theta（权重）
np.random.seed(0)
theta = np.random.rand(n).T # 随机生成10以内的，n维1列的矩阵
# 初始化步长/学习率
alpha = 0.000001
# 初始化迭代误差（用于计算梯度两次迭代的差）
error = np.zeros(n)

# 初始化偏导数矩阵
diff = np.zeros(n)
# 初始化循环次数
count = 0

while count<loop_max:
    count += 1 # 每运行一次count+1，以此来总共记录运行的次数
    # 计算梯度
    for i in  range(m):
        # 计算每个维度theta的梯度，并运算一个梯度更新它，也就是迭代啦
        diff = input_data[i].dot(theta)-y_train[i]
        theta = theta - alpha * diff*(input_data[i])
    # else中将前一个theta赋值给error,theta - error便表示前后两个梯度的变化，当梯度
    #变化很小（在接收的范围内）时，便停止迭代。
    if np.linalg.norm(theta-error) < epsilon:
        break
    else:
        error = theta
print(theta) # 理论上theta = [2,2,3,4]

源码获取：此链接下的SGD.py文件

5.3 小批量梯度下降(MBGD)

"""
 author:jjk
 datetime:2019/9/21
 coding:utf-8
 project name:Pycharm_workstation
 Program function:

"""

import numpy as np

# 构造训练数据集
x_train = np.array([[2, 0., 3], [3, 1., 3], [0, 2., 3], [4, 3., 2], [1, 4., 4]])
m = len(x_train)
x0 = np.full((m, 1), 1)
# 构造一个每个数据第一维特征都是1的矩阵
input_data = np.hstack([x0, x_train])
m, n = input_data.shape
theta1 = np.array([[2, 3, 4]]).T
# 构建标签数据集，后面的np.random.randn是将数据加一点噪声，仪表模拟数据集
# y_train = (input_data.dot(np.array([1, 2, 3, 4]).T)).T
y_train = x_train.dot(theta1) + np.array([[2], [2], [2], [2], [2]])

# 设置两个终止条件
loop_max = 1000000
epsilon = 1e-5
# 初始theta
np.random.seed(0)  # 设置随机种子
theta = np.random.randn(n, 1)  # 随机去一个1维列向量初始化theta

# 初始化步长/学习率
alpha = 0.00001
# 初始化误差，每个维度的theta都应该有一个误差，所以误差是4维
error = np.zeros((n, 1))  # 列向量

# 初始化偏导数
diff = np.zeros((input_data.shape[1], 1))
# 初始化循环次数
count = 0
# 设置小批量的样本数
minibatch_size = 2

while count < loop_max:
    count += 1
    sum_m = np.zeros((n, 1))
    for i in range(1, m, minibatch_size):
        for j in range(i - 1, i + minibatch_size - 1, 1):
            # 计算每个维度的theta
            diff[j] = (input_data[i].dot(theta) - y_train[i]) * input_data[i, j]
        # 求每个维度的梯度的累加和
        sum_m = sum_m + diff
    # 利用这个累加和更新梯度
    theta = theta - alpha * (1.0 / minibatch_size) * sum_m
    # else中将前一个theta赋值给error，theta-error便表示前后两个梯度的变化，当梯度变化小(在接收的范围内)时，便停止迭代

    if np.linalg.norm(theta - error) < epsilon:
        break
    else:
        error = theta
print(theta)  # 输出梯度：真实的应该是2234

源码获取：此链接下的MBGD.py文件

5.4 梯度下降—一元二次函数

"""
 author:jjk
 datetime:2019/9/21
 coding:utf-8
 project name:Pycharm_workstation
 Program function: 一元二次函数-梯度下降变化：0.5, 1.5，2.0，2.5-变化率
"""

import numpy as np
import matplotlib as mpl # 画图
import matplotlib.pyplot as plt
import math # 数学公式
from mpl_toolkits.mplot3d import Axes3D
# 解决中文显示问题
mpl.rcParams['font.sans-serif'] = [u'SimHei']
mpl.rcParams['axes.unicode_minus'] = False

# 一维原始图像
def f1(x):
    return  0.5 * (x-0.25) ** 2 # 1/2*(x-0.25)^2
# 导函数
def h1(x):
    return 0.5 * 2 * (x-0.25) # 原函数求导

# 使用梯度下降法求解
GD_X = []
GD_Y = []
x = 4  # 起始位置
alpha = 0.5  # 学习率

f_change = f1(x) # 调用原始函数
f_current = f_change

GD_X.append(x)
GD_Y.append(f_current)
iter_num = 0
# 变化量大于1e-10并且迭代次数小于100时执行循环体

while f_change >1e-10 and iter_num<100:
    iter_num += 1
    x = x - alpha * h1(x)
    tmp = f1(x)
    f_change = np.abs(f_current-tmp) # 变化量
    f_current = tmp # 此时的函数值
    GD_X.append(x)
    GD_Y.append(f_current)
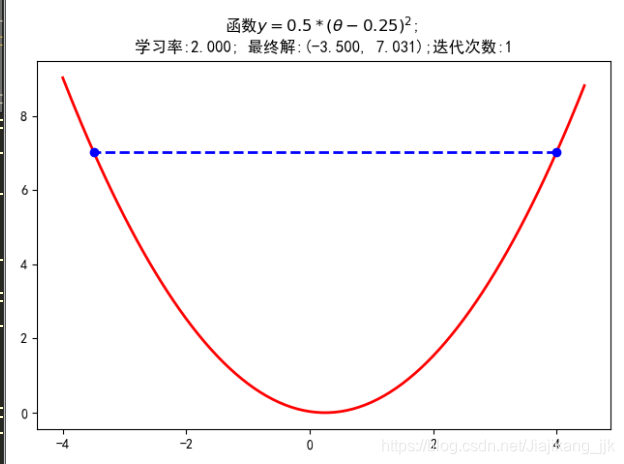
print(u'最终结果为:(%.5f,%.5f)' % (x,f_current))
print(u"迭代过程中x的取值，迭代次数:%d" % iter_num)
print(GD_X)

# 构建数据
X = np.arange(-4, 4.5, 0.05)  # 随机生成-4到4.5，步长为0.05的数
Y = np.array(list(map(lambda t: f1(t), X)))  # X对应的函数值

# 画图
plt.figure(facecolor='w')
plt.plot(X,Y,'r-',linewidth=2) # 函数原图像
plt.plot(GD_X,GD_Y,'bo--',linewidth=2) # 梯度迭代图
plt.title(u'函数$y=0.5 * (θ - 0.25)^2$; \n学习率:%.3f; 最终解:(%.3f, %.3f);迭代次数:%d' % (alpha, x, f_current, iter_num))
plt.show()

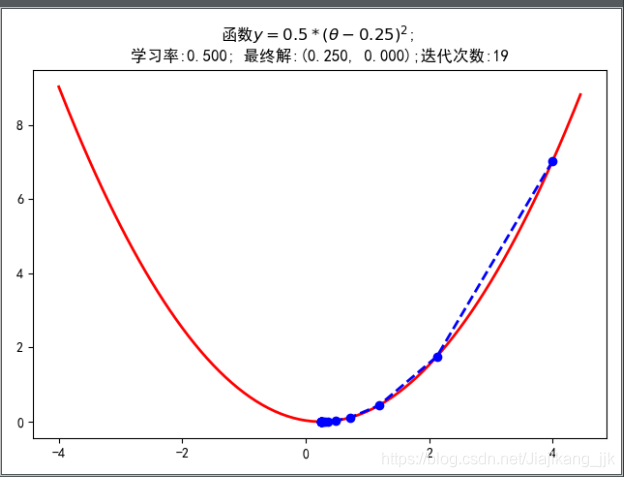
• 学习率比较低的时候，不会出现“之”字型
• 学习率过大，结果不收敛，找不到最小值
  源码获取：此链接下的GD.py文件

5.5 梯度下降—二元二次函数

"""
 author:jjk
 datetime:2019/9/21
 coding:utf-8
 project name:Pycharm_workstation
 Program function:
 
"""
import numpy as np
import  math
import  matplotlib.pyplot as plt
import  matplotlib as mpl
from mpl_toolkits.mplot3d import Axes3D

# 解决中文显示问题
mpl.rcParams['font.sans-serif'] = [u'SimHei']
mpl.rcParams['axes.unicode_minus'] = False


def f2(x,y):
    return  0.6 * (x + y) ** 2 - x * y # 二元函数原型

# 二元函数求导
def hx2(x,y):
    return 0.6 * 2 * (x + y) - y
def hy2(x,y):
    return 0.6 * 2 * (x + y) - x

# 使用梯度下降法求解
GD_X1 = []
GD_X2 = []
GD_Y = []
x1 = 4 # 起始位置
x2 = 4
alpha = 0.5 # 学习率

f_change = f2(x1,x2)
f_current = f_change

GD_X1.append(x1)
GD_X2.append(x2)
GD_Y.append(f_current)
iter_num = 0 # 统计循环次数

while f_change > 1e-10 and iter_num <100:
    iter_num += 1
    prex1 = x1
    prex2 = x2
    x1 = x1 - alpha * hx2(prex1,prex2)
    x2 = x2 - alpha * hy2(prex1,prex2)

    tmp = f2(x1,x2)
    f_change = np.abs(f_current-tmp)
    f_current = tmp
    GD_X1.append(x1) # 迭代
    GD_X2.append(x2)
    GD_Y.append(f_current)

print(u"最终结果为:(%.5f, %.5f, %.5f)" % (x1, x2, f_current))
print(u"迭代过程中X的取值，迭代次数:%d" % iter_num)
print(GD_X1)

# 构建数据
X1 = np.arange(-4,4.5,0.2)
X2 = np.arange(-4,4.5,0.2)
X1,X2 = np.meshgrid(X1,X2)
Y = np.array(list(map(lambda t: f2(t[0], t[1]), zip(X1.flatten(), X2.flatten()))))
Y.shape = X1.shape

# 画图
fig = plt.figure(facecolor='w')
ax = Axes3D(fig)
ax.plot_surface(X1,X2,Y,rstride=1,cstride=1,cmap=plt.cm.jet)
ax.plot(GD_X1,GD_X2,GD_Y,'bo--')

ax.set_title(u'函数$y=0.6 * (θ1 + θ2)^2 - θ1 * θ2$;\n学习率:%.3f; 最终解:(%.3f, %.3f, %.3f);迭代次数:%d' % (alpha, x1, x2, f_current, iter_num))
plt.show()

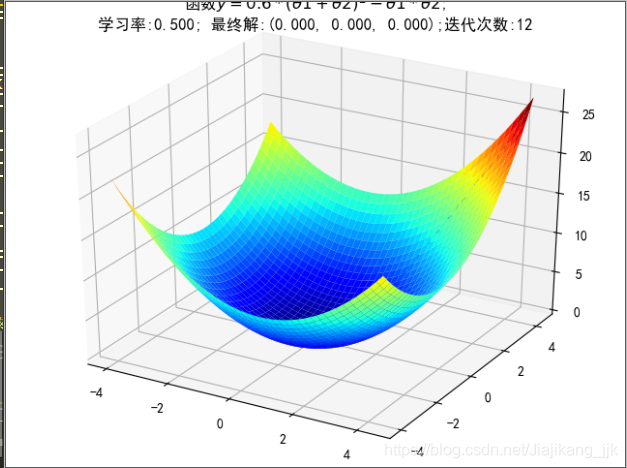
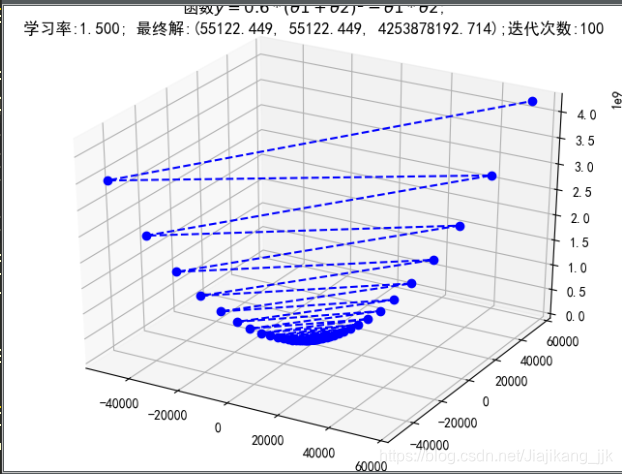
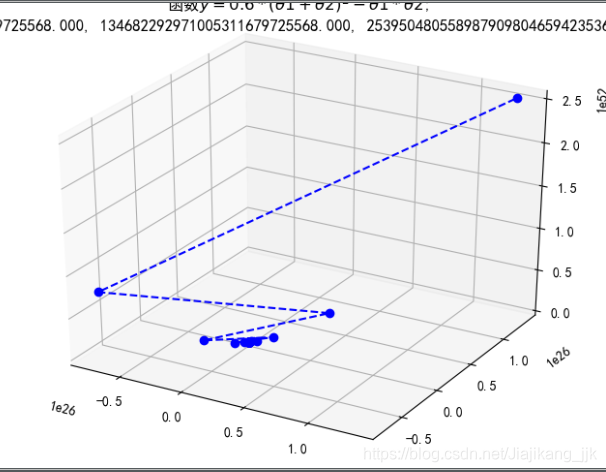
学习率较小时，迭代次数比较小
学习率增大，迭代次数增加
学习率过大，结果不收敛

源码获取：此链接下的GD_02.py文件

好嘛，到了此处关于梯度下降算法的了解和学习就结束了，重点是还得回顾，不然还是会忘~~~
另外，也大量参考了词链接内容。