逻辑回归
之前介绍的线性回归主要用于回归预测,而逻辑回归主要用于分类任务。逻辑回归是在线性回归的基础上,加上了Sigmoid函数。
线性回归的模型是:
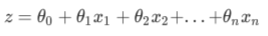
也可以写作:
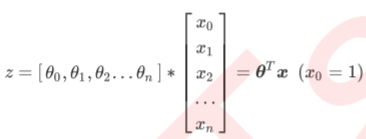
如果需要预测的值是0-1分布的,那么可以引入一个函数,将线性方程z变为g(z),让g(z)的值在(0,1)之间,当g(z)的值接近0时,样本的类别判为类别0;当g(z)的值接近1时,样本的类别判为类别1.
这个函数即为Sigmoid函数。其值域在(0,1)之间,定义域是负无穷到正无穷。
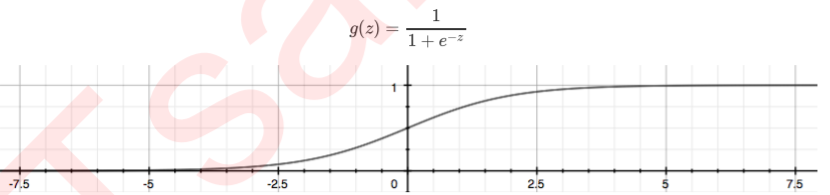

引入Sigmoid函数后,得到了逻辑回归模型的一般形式:
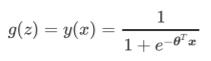
此时,y的取值都在[0,1]之间,因此y和1-y相加必然为1。如果我们令y除以1-y可以得到形似几率(odds)的y/(1-y) ,可看作类别为1的与类别为0的概率比。线性回归的值也就是对数几率。

y(x)的形似几率取对数的本质其实就是我们的线性回归z,我们实际上是在对线性回归模型的预测结果取对数几率,来让其结果无限逼近0和1。
线性回归的任务:通过求解参数构建预测函数z,并希望预测函数z能够尽量拟合数据,
逻辑回归的核心任务也是类似的:求解参数来构建一个能够尽量拟合数据的预测函数y(x),并通过向预测函数中输入特征矩阵来获取相应的标签值y。
y(x)的并非像贝叶斯,输出的是某一类别的概率,它只是(0,1)之间的值,人们近似认为它是概率。一般以0.5为分界点。

逻辑回归的损失函数
二元逻辑回归的标签服从伯努利分布(即0-1分布),因此我们可以将一个特征向量为x,参数为θ的模型中的一个样本i的预测情况表现为如下形式:

当样本i的真实类别为1时,如果P1为1,P0为0,此时预测结果与真实值一致,没有信息损失。若P1为0,P0为1,则预测结果与真实值相反,信息完全损失。反之亦然。

将两种取值的概率整合,可以得到如下等式(单个样本):
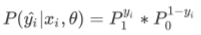
当样本i的真实标签为1时,P0的0次方为1,这个时候P=P1,如果P1为1(P1代表预测值为类别1的概率),模型的效果就好,损失就小;同理,可证样本i的真实标签为0时,如果P0为1(P0代表预测值为类别0的概率),模型的效果就好,损失就小。
所以,为了让模型拟合的好,我们追求的是让P的值为1.而P的本质是样本i由特征向量x和参数θ组成的预测函数中,预测出所有可能的y^的概率,因此1是它的最大值。即我们需要的就是求出P的最大值。这就将模型拟合中的“最小化损失”问题,转换成了对函数求解极值的问题。(找出一组参数,使得P的值达到最大)这个推导过程,其实就是“极大似然法”的推导过程,即通过P值最大化来求参数θ。
所有可能的y^的概率P为:
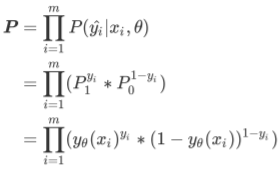
对P取对数:
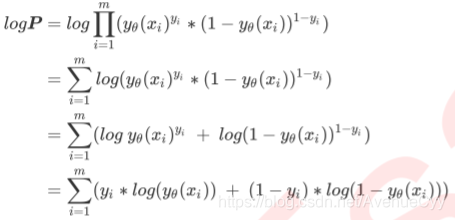
这就是我们的交叉熵函数。为了更好地定义”损失”的含义,我们希望将极大值问题转换为极小值问题,因此我们对log§取负,并且让参数作为函数的自变量,就得到了我们的损失函数J。(将求P的极大值转为求J的极小值)
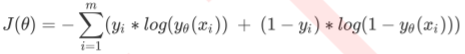
这个是基于逻辑回归返回值的概率性质得出的损失函数。在这个函数上,我们只要追求最小值,就能让模型在训练数据上的拟合效果最好,损失最低。

似然函数和极大似然估计
似然函数:
对于函数:p(x|θ)输入有两个:x表示某一个具体的数据;θ表示模型的参数。
- 如果θ是已知确定的,x是变量,这个函数叫做概率函数(probability function),它描述对于不同的样本点x,其出现概率是多少,求x。
- 如果x是已知确定的,θ是变量,这个函数叫做似然函数(likelihood function), 它描述对于不同的模型参数,出现x这个样本点的概率是多少。求θ。
- 概率函数和似然函数是两个相反的过程。
极大似然估计:
一般投硬币,对于概率来说,是已知该硬币的分布0-1分布,求正反面出现的概率。而对于似然来说,是已知投硬币正反面出现的概率,求该硬币对应的分布。
如何通过已知概率求分布,这时就用到了极大似然估计。其思想是要求得参数让出现的结果(正反面出现的概率)最大,也比较符合我们的正常认知。
举个例子:若我们把投100次硬币出现正面50次,反面50次,记出现正面的概率记为P(投币结果|分布)。
P(投币结果|分布)
=P(x1,x2,…,x100|分布)
=P(x1|分布)P(x2|分布)…P(x100|分布) # 假设每次投硬币结果是独立的。
= P ^ 50 (1-P) ^ 50
此时,P可以取0.5,也可以取0.3,总之P有无数的取值,但是哪种取值和我们投硬币的结果最为相近,最符合常理呢?(我们求的参数是在该分布下,最大化支持出现的结果,即让P值最大化)答案是P=0.5,此时P ^ 50 (1-P) ^ 50的结果最大。可以通过求导,令其导数为0,来求P值。
逻辑回归中的正则化
正则化是用来防止模型过拟合的过程,常用的有L1正则化和L2正则化两种选项,分别通过在损失函数后加上参数向量的L1范式和L2范式的倍数来实现。
损失函数改变,基于损失函数的最优化来求解的参数取值必然改变,我们以此来调节模型拟合的程度。
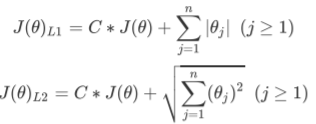
其中:
J是之前的损失函数,
C是用来控制正则化程度的超参数,C越小,损失函数会越小,模型对损失函数的惩罚越重,正则化的效力越强,参数会逐渐被压缩得越来越小。
n是方程中特征的总数,也是方程中参数的总数,
j代表每个参数。在这里,j要大于等于1,是因为我们的参数向量θ中,第一个参数是θ0,是我们的截距,它通常是不参与正则化的。
L1正则化和L2正则化虽然都可以控制过拟合,但它们的效果并不相同。当正则化强度逐渐增大(即C逐渐变小),参数的取值会逐渐变小,但L1正则化会将参数压缩为0(用于特征选择),L2正则化只会让参数尽量小,不会取到0(用于防止过拟合)。(在之前的线性回归中提到过,对参数求偏导后,可以得出该结论)
逻辑回归的特征工程:
对于分类问题选择特征,可考虑使用逻辑回归,因为PCA和SVD的可解释性不强。
逻辑回归对数据的要求低于线性回归,由于我们不是使用最小二乘法来求解,所以逻辑回归对数据的总体分布和方差没有要求,也不需要排除特征之间的共线性。
梯度下降求解逻辑回归
逻辑回归的数学目的是求解能够让模型最优化,拟合程度最好的参数的值,即求解能够让损失函数J最小化的参数值。这里选择用梯度下降法求解。
梯度的定义:


梯度下降:
梯度是一个向量,因此它有大小也有方向。它的大小,就是偏导数组成的向量的大小,又叫做向量的模,记作d。
它的方向,几何上来说,就是损失函数J 的值增加最快的方向。只要沿着梯度向量的反方向移动坐标,损失函数J的取值就会减少得最快,也就最容易找到损失函数的最小值。
在逻辑回归中的损失函数如下:
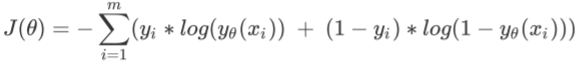
对自变量θ求导,可以得到梯度向量在第j组θ的坐标点上的表示形式:
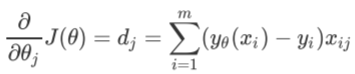
给定一组θ,带入公式,计算得到梯度d。
利用θ和梯度,可以求得下一次迭代的θ+1,整个过程都使得损失函数在不断变小。

步长的概念:
步长的概念,类似于三角形的夹角∠A,取tan值。
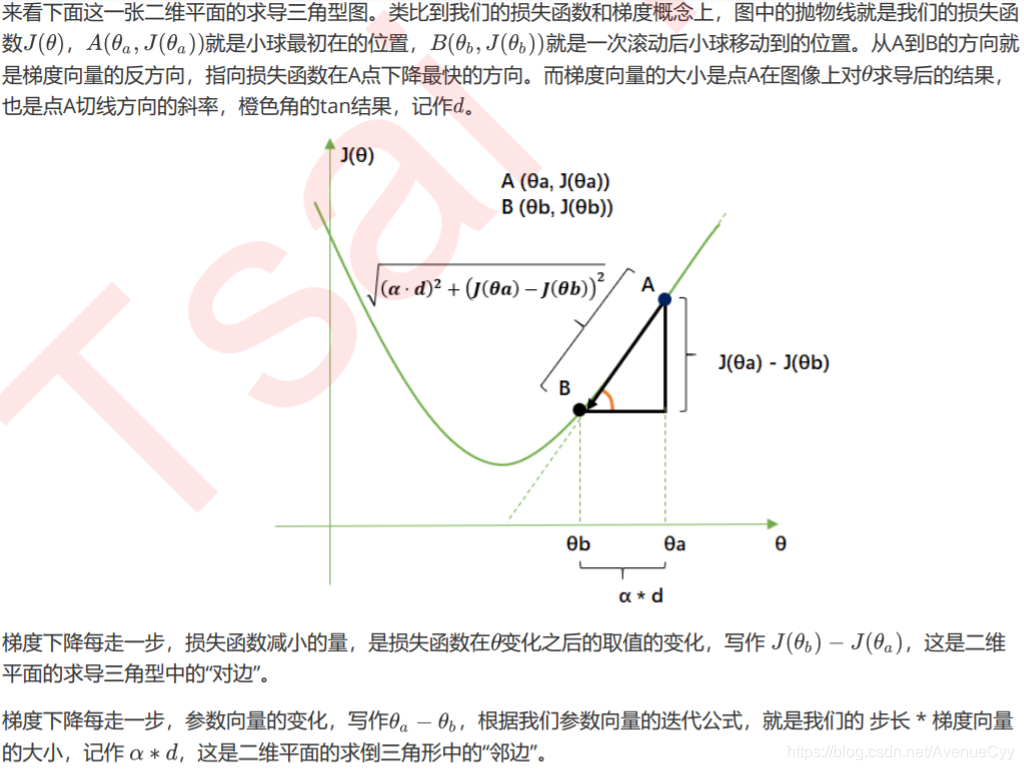

由于参数迭代是靠梯度向量的大小d* 步长a实现的,而J的降低又是靠调节θ来实现的,所以步长可以调节损失函数下降的速率。
在损失函数降低的方向上,步长越长(∠A的值越大),θ的变动就越大,相对的,步长如果很短,θ的每次变动就很小。
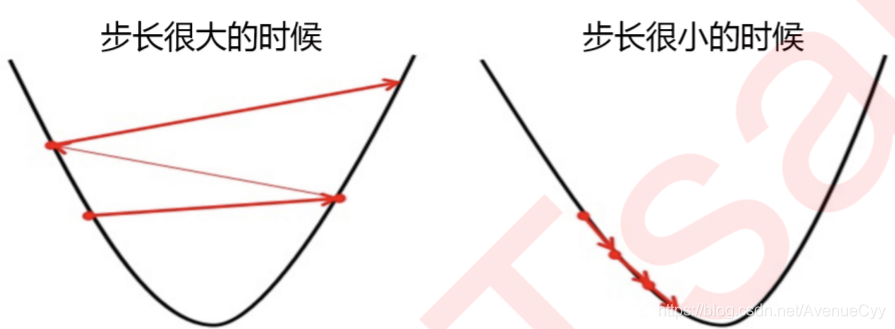
- 步长太大:损失函数下降得就非常快,需要的迭代次数就很少,但梯度下降过程可能跳过损失函数的最低点,无法获取最优值。
- 步长太小:虽然函数会逐渐逼近我们需要的最低点,但迭代的
速度却很缓慢,迭代次数就需要很多。
迭代结束,获取到J的最小值,就可以找出这个最小值对应的参数向量θ,逻辑回归的预测函数也就可以根据这个参数向量θ来建立了。
逻辑回归的数据处理
分类数据
分类数据需要进行标签处理,然后做独热编码处理,这里截取别人做的说明。逻辑回归用于评分卡中,可用WOE来处理分类数据。

数值数据
由于采用最大似然估计法而不是最小二乘法,不用作特殊处理。但可以考虑归一化,加快运算速度。
参考文献
https://zhuanlan.zhihu.com/p/26614750?utm_source=wechat_session&utm_medium=social&utm_oi=672213749885177856
https://www.bilibili.com/video/BV1vJ41187hk?from=search&seid=13147394097118063633
https://www.cnblogs.com/lianyingteng/p/7792693.html
