算法思想:
一、双指针
思想:双指针主要用于遍历数组,两个指针指向不同的元素,从而协同完成任务。
1.排序数组的两数之和(easy 167)
给定一个已按照升序排列 的有序数组,找到两个数使得它们相加之和等于目标数。
函数应该返回这两个下标值 index1 和 index2,其中 index1 必须小于 index2。
说明:
返回的下标值(index1 和 index2)不是从零开始的。
你可以假设每个输入只对应唯一的答案,而且你不可以重复使用相同的元素。
//O(n) O(1)
//使用双指针,一个指针指向值较小的元素,一个指针指向值较大的元素。
//指向较小元素的指针从头向尾遍历,指向较大元素的指针从尾向头遍历。
//如果两个指针指向元素的和 sum == target,那么得到要求的结果;
//如果 sum > target,移动较大的元素,使 sum 变小一些;
//如果 sum < target,移动较小的元素,使 sum 变大一些。
class Solution {
public:
vector<int> twoSum(vector<int>& numbers, int target) {
vector<int> res;
int le=0,ri=numbers.size()-1;
while(le<ri){
int sum=numbers[ri]+numbers[le];
if(sum==target){
res.push_back(le+1);
res.push_back(ri+1);
return res;
}
else if(sum<target){
le++;
}
else{
ri--;
}
}
return res;
}
};
2.平方数之和(easy 633)
给定一个非负整数 c ,你要判断是否存在两个整数 a 和 b,使得 a2 + b2 = c。
//思路与上题一致 j初始设置为c^2
//注意i j sum都用long
class Solution {
public:
bool judgeSquareSum(int c) {
if (c< 0) {return false;}
long i = 0, j = sqrt(c);
while (i <= j) {
long powSum = i * i + j * j;
if (powSum == c) {
return true;
} else if (powSum > c) {
j--;
} else {
i++;
}
}
return false;
}
};
3.反转字符串中的元音字母
编写一个函数,以字符串作为输入,反转该字符串中的元音字母。
示例 1:
输入: “hello”
输出: “holle”
示例 2:
输入: “leetcode”
输出: “leotcede”
说明:
元音字母不包含字母"y"。
//双指针,遇见元音交换
class Solution {
public:
string reverseVowels(string s) {
set<char> vowels={'a', 'e', 'i', 'o', 'u', 'A', 'E', 'I', 'O', 'U'};
int left=0,right=s.size()-1;
while(left<=right){
char cl=s[left];
char cr=s[right];
if(!vowels.count(cl)){
left++;
}
else if(!vowels.count(cr)){
right--;
}
else{
s[left]=cr;
s[right]=cl;
left++;
right--;
}
}
return s;
}
};
4.验证回文字符串II(easy 680)
给定一个非空字符串 s,最多删除一个字符。判断是否能成为回文字符串。
示例 1:
输入: “aba”
输出: True
示例 2:
输入: “abca”
输出: True
解释: 你可以删除c字符。
//O(n) O(1)
//双指针判断两边是否相等,遇到不相等,试着删除一个i或j来继续判断是否回文
class Solution {
public:
bool validPalindrome(string s) {
for(int i=0,j=s.size()-1;i<j;i++,j--){
if(s[i]!=s[j]){
return isPalindrome(s,i+1,j)||isPalindrome(s,i,j-1);
}
}
return true;
}
bool isPalindrome(string s,int i,int j){
while(i<j){
if(s[i++]!=s[j--]){
return false;
}
}
return true;
}
};
5.合并两个有序数组(easy 88)
给你两个有序整数数组 nums1 和 nums2,请你将 nums2 合并到 nums1 中,使 num1 成为一个有序数组。
说明:
初始化 nums1 和 nums2 的元素数量分别为 m 和 n 。
你可以假设 nums1 有足够的空间(空间大小大于或等于 m + n)来保存 nums2 中的元素。
示例:
输入:
nums1 = [1,2,3,0,0,0], m = 3
nums2 = [2,5,6], n = 3
解法一:
一般而言,对于有序数组可以通过 双指针法 达到O(n + m)的时间复杂度。
最直接的算法实现是将指针p1 置为 nums1的开头, p2为 nums2的开头,在每一步将最小值放入输出数组中。
由于 nums1 是用于输出的数组,需要将nums1中的前m个元素放在其他地方,也就需要 O(m)的空间复杂度。
class Solution {
public:
void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
vector<int> numscp1=nums1;
int i=0,j=0,p=0;
while(i<m&& j<n){
nums1[p++] = (numscp1[i] < nums2[j]) ? numscp1[i++] : nums2[j++];
}
while(i<m){
nums1[p++]=numscp1[i++];
}
while(j<n){
nums1[p++]=nums2[j++];
}
}
};
解法二:
解法一的延伸版:如果从结尾开始改写 nums1 的值这里没有信息,因此不需要额外空间。

//Java版本
class Solution {
public void merge(int[] nums1, int m, int[] nums2, int n) {
// two get pointers for nums1 and nums2
int p1 = m - 1;
int p2 = n - 1;
// set pointer for nums1
int p = m + n - 1;
// while there are still elements to compare
while ((p1 >= 0) && (p2 >= 0))
// compare two elements from nums1 and nums2
// and add the largest one in nums1
nums1[p--] = (nums1[p1] < nums2[p2]) ? nums2[p2--] : nums1[p1--];
// add missing elements from nums2
System.arraycopy(nums2, 0, nums1, 0, p2 + 1);
}
}
6.判断环形链表
给定一个链表,判断链表中是否有环。
为了表示给定链表中的环,我们使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。 如果 pos 是 -1,则在该链表中没有环。
思路一:
使用两个slow, fast指针从头开始扫描链表。指针slow 每次走1步,指针fast每次走2步。如果存在环,则指针slow、fast会相遇;如果不存在环,指针fast遇到NULL退出。。
放一个证明 证明此方法判断单链表有环的正确性
//O(n) O(1)
class Solution {
public:
bool hasCycle(ListNode *head) {
if(head==NULL){return false;}
ListNode* l1=head;
ListNode* l2=head->next;
while(l1!=NULL && l2!=NULL && l2->next!=NULL){
if(l1==l2){
return true;
}
l1=l1->next;
l2=l2->next->next;
}
return false;
}
};
思路2:
遍历所有结点并在哈希表中存储每个结点的引用(或内存地址)。如果当前结点为空结点 null(即已检测到链表尾部的下一个结点),那么我们已经遍历完整个链表,并且该链表不是环形链表。如果当前结点的引用已经存在于哈希表中,那么返回 true(即该链表为环形链表)。
//O(n) O(1)
class Solution {
public:
bool hasCycle(ListNode *head) {
set<ListNode*> s;
while(head!=NULL){
if(s.count(head)){
return true;
}
else{
s.insert(head);
}
head=head->next;
}
return false;
}
};
7.通过删除字母匹配到字典中最长的单词(medium 524)
给定一个字符串和一个字符串字典,找到字典里面最长的字符串,该字符串可以通过删除给定字符串的某些字符来得到。如果答案不止一个,返回长度最长且字典顺序最小的字符串。如果答案不存在,则返回空字符串。
示例 1:
输入:
s = “abpcplea”, d = [“ale”,“apple”,“monkey”,“plea”]
输出:
“apple”
思路:
其实是一个最长子序列问题。通过删除字符串 s 中的一个字符能得到字符串 t,可以认为 t 是 s 的子序列,我们可以使用双指针来判断一个字符串是否为另一个字符串的子序列。
class Solution {
public:
//前提是可以通过删除s中得字符,直接得到target,说明顺序相同,只是插入了其他字母
string findLongestWord(string s, vector<string>& d) {
//定义变量储存最大值
string longestStr="";
//遍历容器
for(int i=0;i<d.size();i++){
//如果比当前最长已经匹配的单词还短,一定不是
if(longestStr.size()>d[i].size()){
continue;
}
//如果一样长顺序更大,一定不是,这里compare是比较了两个字符串的顺序大小
if(d[i].size()==longestStr.size() && longestStr.compare(d[i])<0){
continue;
}
//如果是子序列,储存最大
if(SubString(s,d[i])){
longestStr=d[i];
}
}
return longestStr;
}
//双指针判断是否是子序列
bool SubString(string s,string target){
int i=0,j=0;
while(i<s.length()&&j<target.length()){
//相同两个指针都后移一位
if(s[i]==target[j]){
j++;
}
//如果不相同,删除相当于s后移一位指针
i++;
}
if(j==target.length()){
return true;
}
return false;
}
};
二、二分查找
二分查找也称为折半查找,每次都能将查找区间减半,这种折半特性的算法时间复杂度为 O(logN)。 有序
正常实现代码
Input : [1,2,3,4,5]
key : 3
return the index : 2
public int binarySearch(int[] nums, int key) {
int l = 0, h = nums.length - 1;
while (l <= h) {
int m = l + (h - l) / 2;
if (nums[m] == key) {
return m;
} else if (nums[m] > key) {
h = m - 1;
} else {
l = m + 1;
}
}
return -1;
}
中值m的计算:有两种计算中值 m 的方式:
m = (l + h) / 2
m = l + (h - l) / 2
l + h 可能出现加法溢出,也就是说加法的结果大于整型能够表示的范围。但是 l 和 h 都为正数,因此 h - l 不会出现加法溢出问题。所以,最好使用第二种计算法方法。
未成功查找的返回值
循环退出时如果仍然没有查找到 key,那么表示查找失败。可以有两种返回值:
(1)-1:以一个错误码表示没有查找到 key
(2) l:将 key 插入到 nums 中的正确位置
变种
二分查找可以有很多变种,实现变种要注意边界值的判断。例如在一个有重复元素的数组中查找 key 的最左位置的实现如下:
public int binarySearch(int[] nums, int key) {
int l = 0, h = nums.length - 1;
while (l < h) {
int m = l + (h - l) / 2;
if (nums[m] >= key) {
h = m;
} else {
l = m + 1;
}
}
return l;
}
该实现和正常实现有以下不同:
h 的赋值表达式为 h = m
循环条件为 l < h
最后返回 l 而不是 -1
在 nums[m] >= key 的情况下,可以推导出最左 key 位于 [l, m] 区间中,这是一个闭区间。h 的赋值表达式为 h = m,因为 m 位置也可能是解。
在 h 的赋值表达式为 h = m 的情况下,如果循环条件为 l <= h,那么会出现循环无法退出的情况,因此循环条件只能是 l < h。以下演示了循环条件为 l <= h 时循环无法退出的情况:
nums = {0, 1, 2}, key = 1
l m h
0 1 2 nums[m] >= key
0 0 1 nums[m] < key
1 1 1 nums[m] >= key
1 1 1 nums[m] >= key
…
当循环体退出时,不表示没有查找到 key,因此最后返回的结果不应该为 -1。为了验证有没有查找到,需要在调用端判断一下返回位置上的值和 key 是否相等。
8.x的平方根(easy 69)
实现 int sqrt(int x) 函数。
计算并返回 x 的平方根,其中 x 是非负整数。
由于返回类型是整数,结果只保留整数的部分,小数部分将被舍去。
思路1:
一个数 x 的开方 sqrt 一定在 0 ~ x 之间,并且满足 sqrt == x / sqrt。可以利用二分查找在 0 ~ x 之间查找 sqrt。
对于 x = 8,它的开方是 2.82842…,最后应该返回 2 而不是 3。在循环条件为 l <= h 并且循环退出时,h 总是比 l 小 1,也就是说 h = 2,l = 3,因此最后的返回值应该为 h 而不是 l。
class Solution {
public:
int mySqrt(int x) {
if(x<=1){return x;}
int l=1,h=x;
while(l<=h){
int mid=l+(h-l)/2;
if(mid==(x/mid)){
return mid;
}
else if(mid<(x/mid)){
l=mid+1;
}
else{
h=mid-1;
}
}
return h;
}
};
9.寻找比目标字母大的最小字母
给定一个只包含小写字母的有序数组letters 和一个目标字母 target,寻找有序数组里面比目标字母大的最小字母。
//法一:有序,所以直接扫描,遇到比目标大的就是
//O(n) O(1)
class Solution {
public:
char nextGreatestLetter(vector<char>& letters, char target) {
for(int i=0;i<letters.size();i++){
if(letters[i]>target){
return letters[i];
}
}
return letters[0];
}
};
法2:二分查找,只需将target插入正确的位置,l即是target右边的第一个位置
O(logn) O(1)
class Solution {
public:
char nextGreatestLetter(vector<char>& letters, char target) {
int l=0,h=letters.size()-1;
while(l<=h){
int mid=l+(h-l)/2;
if(letters[mid]<=target){
l=mid+1;
}
else{
h=mid-1;
}
}
return l<letters.size()?letters[l]:letters[0]; //若l>总长,说明target插在末尾,返回第一个字符
}
};
给定一个只包含整数的有序数组,每个元素都会出现两次,唯有一个数只会出现一次,找出这个数。
示例 1:
输入: [1,1,2,3,3,4,4,8,8]
输出: 2
注意: 您的方案应该在 O(log n)时间复杂度和 O(1)空间复杂度中运行。
思路:
看见时间复杂度要求就知道要用二分查找了
数组:[1,1,2,2,3,4,4,8,8]
下标:[0,1,2,3,4,5,6,7,8]
令 index 为 单元素在数组中的位置。在 index 之后,数组中原来存在的成对状态被改变。如果 m 为偶数,并且 m + 1 < index,那么 nums[m] == nums[m + 1];m + 1 >= index,那么 nums[m] != nums[m + 1]。
从上面的规律可以知道,令m为偶数,如果 nums[m] == nums[m + 1],那么 index 所在的数组位置为 [m + 2, h],此时令 l = m + 2;如果 nums[m] != nums[m + 1],那么 index 所在的数组位置为 [l, m],此时令 h = m。
因为 h 的赋值表达式为 h = m,那么循环条件也就只能使用 l < h 这种形式。
//O(log(n/2) 仅仅对偶数进行搜索
class Solution {
public:
int singleNonDuplicate(vector<int>& nums) {
int l=0,h=nums.size()-1;
while(l<h){
int mid=l+(h-l)/2;
if(mid%2==1){ //使m保持为该对相同数的偶数下标
mid--;
}
if(nums[mid]==nums[mid+1]){
l=mid+2;
}
else{
h=mid;
}
}
return nums[l];
}
};
11.旋转数组中的最小值(medium 153)
假设按照升序排序的数组在预先未知的某个点上进行了旋转。
( 例如,数组 [0,1,2,4,5,6,7] 可能变为 [4,5,6,7,0,1,2] )。
请找出其中最小的元素。
你可以假设数组中不存在重复元素。
示例 1:
输入: [3,4,5,1,2]
输出: 1
//O(logN)
class Solution {
public:
int findMin(vector<int>& nums) {
int l=0,h=nums.size()-1;
while(l<h){
int mid=l+(h-l)/2;
if(nums[mid]<=nums[h]){
h=mid;
}
else{
l=mid+1;
}
}
return nums[l];
}
};
若是非递减数组,存在重复元素,例如出现1101111这样的,mid=h,只能h–,挨个查找
class Solution {
public:
int findMin(vector<int>& nums) {
int l=0,h=nums.size()-1;
while(l<h){
int mid=l+(h-l)/2;
if(nums[mid]<nums[h]){
h=mid;
}
else if(nums[mid]>nums[h]) {
l=mid+1;
}
else{
h--; //防止类似1101111这种情况出现
}
}
return nums[l];
}
};
12.在排序数组中查找目标元素的第一个位置和最后一个位置(medium 34)
给定一个按照升序排列的整数数组 nums,和一个目标值 target。找出给定目标值在数组中的开始位置和结束位置。
你的算法时间复杂度必须是 O(log n) 级别。
如果数组中不存在目标值,返回 [-1, -1]。
示例 1:
输入: nums = [5,7,7,8,8,10], target = 8
输出: [3,4]
思路:
可以用二分查找找出第一个位置和最后一个位置,但是寻找的方法有所不同,需要实现两个二分查找。我们将寻找 target 最后一个位置,转换成寻找 target+1 第一个位置,再往前移动一个位置。这样我们只需要实现一个二分查找代码即可。
注意
在寻找第一个位置的二分查找代码中,需要注意 h 的取值为 nums.length,而不是 nums.length - 1。先看以下示例:
nums = [2,2], target = 2
如果 h 的取值为 nums.length - 1,那么 last = findFirst(nums, target + 1) - 1 = 1 - 1 = 0。这是因为 findLeft 只会返回 [0, nums.length - 1] 范围的值,对于 findFirst([2,2], 3) ,我们希望返回 3 插入 nums 中的位置,也就是数组最后一个位置再往后一个位置,即 nums.length。所以我们需要将 h 取值为 nums.length,从而使得 findFirst返回的区间更大,能够覆盖 target 大于 nums 最后一个元素的情况。
class Solution {
public:
vector<int> searchRange(vector<int>& nums, int target) {
vector<int> res;
int first = findFirst(nums, target);
int last = findFirst(nums, target + 1) - 1;
if (first == nums.size() || nums[first] != target) {
res.push_back(-1);
res.push_back(-1);
}
else {
res.push_back(first);
res.push_back(last);
}
return res;
}
private:
int findFirst(vector<int>& nums, int target) {
int l = 0, h = nums.size(); // 注意 h 的初始值
while (l < h) {
int m = l + (h - l) / 2;
if (nums[m] >= target) {
h = m;
}
else {
l = m + 1;
}
}
return l;
}
};
也可以用两次二分法,分别查找左边界和右边界
lass Solution {
public:
vector<int> searchRange(vector<int>& nums, int target) {
vector<int> res(2,-1);
if(nums.empty()) return res;
int n=nums.size(),l=0,r=n-1;
while(l<r){
int m=l+(r-l)/2;
if(nums[m]>=target) r=m;
else l=m+1;
}
if(nums[l]!=target) return res;
res[0]=l;
r=n; //注意此处r=n,第二次找的是最后一个位置+1的位置,有可能超出边界,覆盖 target 大于 nums 最后一个元素的情况。可以看下C++ upper_bound的实现
while(l<r){
int m=l+(r-l)/2;
if(nums[m]<=target) l=m+1;
else r=m;
}
res[1]=l-1;
return res;
}
};
插入一个大佬总结的好用的二分法查找模板
用“排除法”(减治思想)写二分查找问题、与其它二分查找模板的比较
三.排序
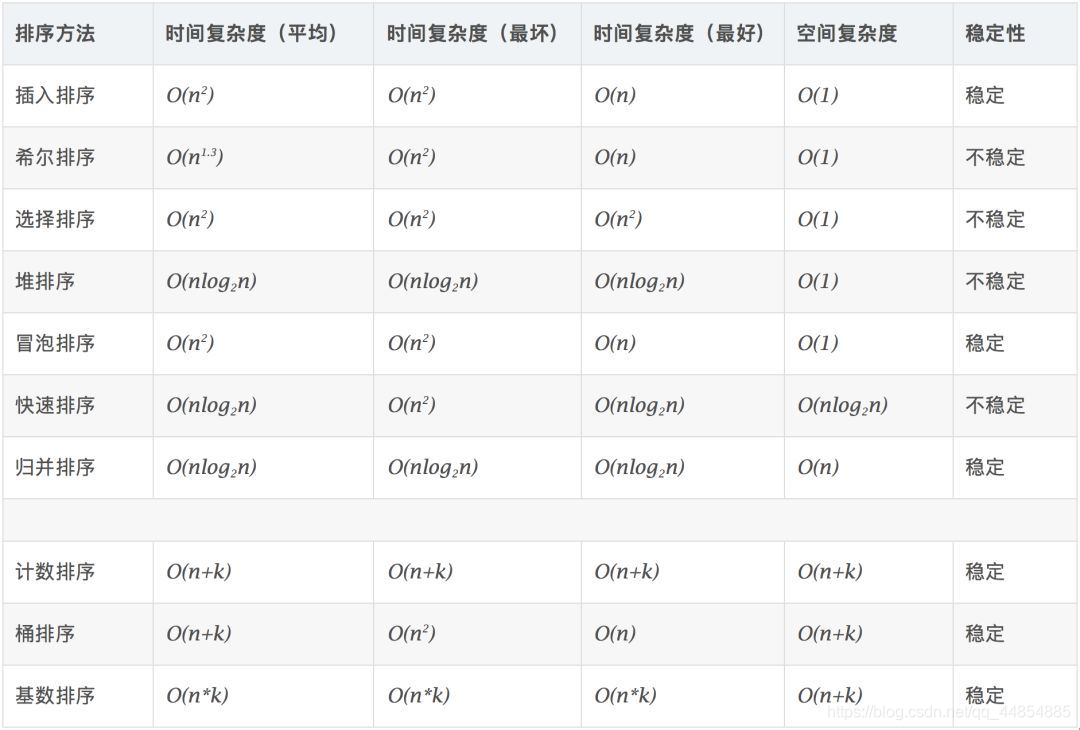
(1)数据结构 堆
堆就是用数组实现的二叉树,所有它没有使用父指针或者子指针。堆根据“堆属性”来排序,“堆属性”决定了树中节点的位置。
数据结构:堆的详细介绍及操作
堆的常用方法:
构建优先队列
支持堆排序
快速找出一个集合中的最小值(或者最大值)
堆分为两种:最大堆和最小堆,两者的差别在于节点的排序方式。
在最大堆中,父节点的值比每一个子节点的值都要大。在最小堆中,父节点的值比每一个子节点的值都要小。这就是所谓的“堆属性”,并且这个属性对堆中的每一个节点都成立。最大堆:
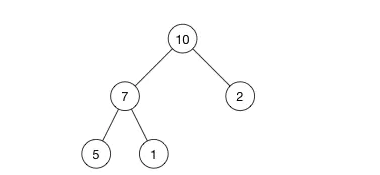
堆的存储:[ 10, 7, 2, 5, 1 ]
堆中父节点和子节点的关系
parent(i) = floor((i - 1)/2)
left(i) = 2i + 1
right(i) = 2i + 2
最大堆:array[parent(i)] >= array[i]
注意:在堆中,在当前层级所有的节点都已经填满之前不允许开是下一层的填充,
cpp中:构建最小堆(小顶堆)
priority_queue<int, vector<int>, greater<int>> pq;
构建大顶堆:
priority_queue<int, vector<int>, less<int>> pq;
有两个原始操作用于保证插入或删除节点以后堆是一个有效的最大堆或者最小堆:
shiftUp(): 如果一个节点比它的父节点大(最大堆)或者小(最小堆),那么需要将它同父节点交换位置。这样是这个节点在数组的位置上升。
shiftDown(): 如果一个节点比它的子节点小(最大堆)或者大(最小堆),那么需要将它向下移动。这个操作也称作“堆化(heapify)”。
shiftUp 或者 shiftDown 是一个递归的过程,所以它的时间复杂度是 **O(log n)。**
其它删除 插入等操作都是基于这两个原始操作
(2选择排序
1.在一个长度为 N 的无序数组中,第一次遍历 n-1 个数找到最小的和第一个数交换。
2.第二次从下一个数开始遍历 n-2 个数,找到最小的数和第二个数交换。
3.重复以上操作直到第 n-1 次遍历最小的数和第 n-1 个数交换,排序完成。
时间复杂度O(n^2)
(3)快速选择排序(partition)
快速选择排序:是一个在平均情况下的时间复杂度为O(nlogn),最坏的时间复杂度为O(n^{2}) ,且是一个不稳定的排序方法,但一般情况下它的排序速度很快,只有当数据基本有序的时候速度是最慢的。
排序的过程:
1 一般选择待排序表中的第一个记录作为基准数,然后初始化两个指针 low 和 high ,分别指向表的上界和下界
2 从表的最右侧开始依次向左搜索,找到第一个关键字小于基准数的记录,将其移到 low 处并high--。
3 接着从表的最左侧位置开始依次向右边搜索,找到第一个大于基准数的记录,将其移到 high 的位置后 low++.
4 重复操作2和3,直至 low 和 high 相等,此时 low 和 high 的位置即为基准数在此序列中的最终位置。
5 通过递归调用把小于基准元素和大于基准元素的子序列进行排序。
void quick_sort(int low, int high)
{
if(low < high)
{
//有些快速选择排序是将中间的值作为基准数作为排序,这样当数据基本有序的时候可以降低运行时间 swap(s[low], s[(low + high) / 2]);
int i = low, j = high, x = s[low];
while(i < j)
{
while(i < j && s[j] >= x) //从右往左找第一个小于x的数
j--;
if(i < j) //跟左边的l位置上进行交换
s[i++] = s[j];
while(i < j && s[i] < x) //从左往右找第一个大于或等于x的数
i++;
if(i < j) //同理
s[j--] = s[i];
}
s[i] = x; //注意最后排序好后要将基准数填进去
quick_sort(a, low, i - 1); //递归排序左边的区间
quick_sort(a, i + 1, high); //递归排序右边的区间
}
}
另一种写法的快排:这一种方法是从左右两个方向同时进行的快排(速度更快)
//例 从初始序列“6 1 2 7 9 3 4 5 10 8”两端开始“探测”。先从右往左找一个小于6的数,再从左往右找一个大于6的数,然后**交换**他们。
//第一次交换结束。接下来开始哨兵j继续向左挪动(再友情提醒,每次必须是哨兵j先出发)。
//他发现了4(比基准数6要小,满足要求)之后停了下来。哨兵i也继续向右挪动的,
//他发现了9(比基准数6要大,满足要求)之后停了下来。此时再次进行交换
//第二次交换结束,“探测”继续。哨兵j继续向左挪动,他发现了3之后又停了下来。
//哨兵i继续向右移动.此时哨兵i和哨兵j相遇了,哨兵i和哨兵j都走到3面前。说明此时“探测”结束。我们将基准数6和3进行交换.
//到此第一轮“探测”真正结束。此时以基准数6为分界点,6左边的数都小于等于6,6右边的数都大于等于6
void quick_sort(int l, int r)
{
int i = l, j = r, m = a[(l+r)/2];
while(i <= j)
{
while(a[j] > m)
j--;
while(a[i] < m)
i++;
if(i <= j)
{
swap(a[i], a[j]);
i++;
j--;
}
}
//至此,i > j, l 到 j 部分为小于基准数, i 到 r 部分为大于基准数
if(l < j)
quick_sort(l, j);
if(i < r)
quick_sort(i, r);
}
1.数组中第K大的元素(medium 215)
在未排序的数组中找到第 k 个最大的元素。请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。
示例 1:
输入: [3,2,1,5,6,4] 和 k = 2
输出: 5
法一:
//堆排序,创建小顶堆
//大小为 k 的堆中添加元素的时间复杂度为 O(logk),我们将重复该操作 N 次,故总时间复杂度为 O(Nlogk)。
//空间复杂度 : O(k),用于存储堆元素
class Solution {
public:
int findKthLargest(vector<int>& nums, int k) {
priority_queue<int, vector<int>, greater<int>> pq; //构建最小堆
for (auto& n : nums){
pq.push(n);
if (pq.size() > k){
pq.pop();
}
}
return pq.top();
}
};
法2.快速选择排序
四、分治算法思想
“分而治之”,就是把一个复杂的问题分成两个或更多的相同或相似的子问题,再把子问题分成更小的子问题……直到最后子问题可以简单的直接求解,原问题的解即子问题的解的合并。
(1)为运算符表达式设计优先级(241 medium)
给定一个含有数字和运算符的字符串,为表达式添加括号,改变其运算优先级以求出不同的结果。你需要给出所有可能的组合的结果。有效的运算符号包含 +, - 以及 * 。
示例 1:
输入: “2-1-1”
输出: [0, 2]
解释:
((2-1)-1) = 0
(2-(1-1)) = 2
分治思想分解过程
输入:23-45
以运算符为分界
第一步的分解:a:2和3-45;b:23和45;c:23-4和5;
第二部的细分:a部分:左边:直接返回2 右边:在分解,aa:3和45,ab:3-4和5
补充:同一个符号的左右各会产生至少一个,至多多个数值。左多个数和右多个数进行运算(两个循环搞定所有结果) 如a:2和3-45 ,左边产生2,右边产生-5和-17,那么a这一级最终有-10,-34两个数值。
class Solution {
public:
vector<int> diffWaysToCompute(string input) {
vector<int> res;
for(int i=0;i<input.size();i++){
if(input[i]=='+'||input[i]=='-'||input[i]=='*'){
//分治关键,以运算符作为分界
vector<int> preNums=diffWaysToCompute(input.substr(0,i));
vector<int> posNums=diffWaysToCompute(input.substr(i+1));
for(int j=0;j<preNums.size();j++){ //此处注意多重
for(int k=0;k<posNums.size();k++){ //的for循环,这是为了应对结果中的多运算符情况
int pre=preNums[j];
int pos=posNums[k];
switch (input[i]){
case '+':
res.push_back(pre+pos);
break;
case '-':
res.push_back(pre-pos);
break;
case '*':
res.push_back(pre*pos);
break;
}
}
}
}
}
//这个退出条件很重要,比如单元素时,就以此判断而得以退出
if(res.empty()){
int num=stoi(input);
res.push_back(num);
}
return res;
}
};
五.贪心算法
贪心算法一般用来解决需要 “找到要做某事的最小数量” 或 “找到在某些情况下适合的最大物品数量” 的问题,且提供的是无序的输入。
贪心算法的思想是每一步都选择最佳解决方案,最终获得全局最佳的解决方案。
标准解决方案具有 O(NlogN) 的时间复杂度且由以下两部分组成:
1.思考如何排序输入数据(\mathcal{O}(N \log N)O(NlogN) 的时间复杂度)。
2.思考如何解析排序后的数据O(N) 的时间复杂度)
如果输入数据本身有序,则我们不需要进行排序,那么该贪心算法具有 O(N) 的时间复杂度。
如何证明你的贪心思想具有全局最优的效果:可以使用反证法来证明。
1.分发饼干(easy 455)
假设你是一位很棒的家长,想要给你的孩子们一些小饼干。但是,每个孩子最多只能给一块饼干。对每个孩子 i ,都有一个胃口值 gi ,这是能让孩子们满足胃口的饼干的最小尺寸;并且每块饼干 j ,都有一个尺寸 sj 。如果 sj >= gi ,我们可以将这个饼干 j 分配给孩子 i ,这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子,并输出这个最大数值。
注意:
你可以假设胃口值为正。
一个小朋友最多只能拥有一块饼干。
示例 1:
输入: [1,2,3], [1,1]
输出: 1
解析:
1.给一个孩子的饼干应当尽量小并且又能满足该孩子,这样大饼干才能拿来给满足度比较大的孩子。
2.因为满足度最小的孩子最容易得到满足,所以先满足满足度最小的孩子。
在以上的解法中,我们只在每次分配时饼干时选择一种看起来是当前最优的分配方法,但无法保证这种局部最优的分配方法最后能得到全局最优解。我们假设能得到全局最优解,并使用反证法进行证明,即假设存在一种比我们使用的贪心策略更优的最优策略。如果不存在这种最优策略,表示贪心策略就是最优策略,得到的解也就是全局最优解。
证明:假设在某次选择中,贪心策略选择给当前满足度最小的孩子分配第 m 个饼干,第 m 个饼干为可以满足该孩子的最小饼干。假设存在一种最优策略,可以给该孩子分配第 n 个饼干,并且 m < n。我们可以发现,经过这一轮分配,贪心策略分配后剩下的饼干一定有一个比最优策略来得大。因此在后续的分配中,贪心策略一定能满足更多的孩子。也就是说不存在比贪心策略更优的策略,即贪心策略就是最优策略。
//时间复杂度:O(Nlog(N)),排序算法的复杂度
//空间复杂度:O(1)
class Solution {
public:
int findContentChildren(vector<int>& g, vector<int>& s) {
sort(s.begin(),s.end());
sort(g.begin(),g.end());
int i=0,j=0;
while(i<g.size()&&j<s.size()){
if(g[i]<=s[j]){
i++;
}
j++;
}
return i;
}
};
2.无重叠区间(mediu,435)
给定一个区间的集合,找到需要移除区间的最小数量,使剩余区间互不重叠。
注意:
可以认为区间的终点总是大于它的起点。
区间 [1,2] 和 [2,3] 的边界相互“接触”,但没有相互重叠。
示例 1:
输入: [ [1,2], [2,3], [3,4], [1,3] ]
输出: 1
解释: 移除 [1,3] 后,剩下的区间没有重叠。
思路:
先计算最多能组成的不重叠区间个数,然后用区间总个数减去不重叠区间的个数。
在每次选择中,区间的结尾最为重要,选择的区间结尾越小,留给后面的区间的空间越大,那么后面能够选择的区间个数也就越大。
按区间的结尾进行排序,每次选择结尾最小,并且和前一个区间不重叠的区间。
//时间复杂度:O(nlog(n))。排序需要O(nlog(n)) 的时间。
//空间复杂度:O(1)
class Solution {
public:
int eraseOverlapIntervals(vector<vector<int>>& intervals) {
if(intervals.size()==0){return 0;}
//按结尾对区间进行排序
sort(intervals.begin(), intervals.end(),
[&](const vector<int> & i1, const vector<int> & i2){
return i1[1] < i2[1];
});
int count=1;
int end=intervals[0][1];
for(int i=1;i<intervals.size();i++){
if(intervals[i][0]<end){
continue;
}
else{
end=intervals[i][1];
count++;
}
}
return intervals.size()-count;
}
};
3.用最少数量的箭引爆气球(medium 452)
在二维空间中有许多球形的气球。对于每个气球,提供的输入是水平方向上,气球直径的开始和结束坐标。由于它是水平的,所以y坐标并不重要,因此只要知道开始和结束的x坐标就足够了。开始坐标总是小于结束坐标。平面内最多存在104个气球。
一支弓箭可以沿着x轴从不同点完全垂直地射出。在坐标x处射出一支箭,若有一个气球的直径的开始和结束坐标为 xstart,xend, 且满足 xstart ≤ x ≤ xend,则该气球会被引爆。可以射出的弓箭的数量没有限制。 弓箭一旦被射出之后,可以无限地前进。我们想找到使得所有气球全部被引爆,所需的弓箭的最小数量。
Example:
输入:
[[10,16], [2,8], [1,6], [7,12]]
输出:
2
解释:
对于该样例,我们可以在x = 6(射爆[2,8],[1,6]两个气球)和 x = 11(射爆另外两个气球)
思路:
我们可以跟踪气球的结束坐标,若下个气球开始坐标在当前气球的结束坐标前,则我们可以用一支箭一起引爆;若下个气球的开始坐标在当前气球的结束坐标后,则我们必须增加箭的数量。并跟踪下个气球的结束坐标。
所以也是计算不重叠的区间个数,跟上一题思路一样,不过和 Non-overlapping Intervals 的区别在于,[1, 2] 和 [2, 3] 在本题中算是重叠区间。
class Solution {
public:
int findMinArrowShots(vector<vector<int>>& points) {
if(points.size()==0){return 0;}
//按结尾对区间进行排序
sort(points.begin(), points.end(),
[&](const vector<int> & i1, const vector<int> & i2){
return i1[1] < i2[1];
});
int count=1;
int end=points[0][1];
for(int i=1;i<points.size();i++){
if(points[i][0]<=end){ //
continue;
}
else{
end=points[i][1];
count++;
}
}
return count;
}
};
4.根据身高重建队列(medium 406)
假设有打乱顺序的一群人站成一个队列。 每个人由一个整数对(h, k)表示,其中h是这个人的身高,k是排在这个人前面且身高大于或等于h的人数。 编写一个算法来重建这个队列。
注意:
总人数少于1100人。
示例
输入:
[[7,0], [4,4], [7,1], [5,0], [6,1], [5,2]]
输出:
[[5,0], [7,0], [5,2], [6,1], [4,4], [7,1]]
思路:
核心思路非常简单:
先排身高更高的,这是要防止后排入人员影响先排入人员位置
每次排入新人员[h,k]时,已处于队列的人身高都>=h,所以新排入位置就是people[k]
有了这两个思路代码实现就非常简单了
先将people按照身高降序排序,又由于每次插入的位置是k,所以相同身高需要按k升序排序,否则插入位置会越界
由于后续需要频繁使用insert()操作,建议使用list作为中间容器
循环地从头读取people,根据people[i][1]也就是k,插入list,注意list的迭代器不支持随机访问,需要使用advance()找到应插入位置
将完成所有插入操作的list重建为vector返回
// 先排序
// [7,0], [7,1], [6,1], [5,0], [5,2], [4,4]
// 再一个一个插入。
// [7,0]
// [7,0], [7,1]
// [7,0], [6,1], [7,1]
// [5,0], [7,0], [6,1], [7,1]
// [5,0], [7,0], [5,2], [6,1], [7,1]
// [5,0], [7,0], [5,2], [6,1], [4,4], [7,1]
sort(people.begin(), people.end(), [](const vector<int>& a, const vector<int>& b) {
if (a[0] > b[0]) return true;
if (a[0] == b[0] && a[1] < b[1]) return true;
return false;
});
vector<vector<int>> res;
for (auto& e : people) {
res.insert(res.begin() + e[1], e);
}
return res;
}
};
5.买卖股票的最佳时机(easy 121)
给定一个数组,它的第 i 个元素是一支给定股票第 i 天的价格。
如果你最多只允许完成一笔交易(即买入和卖出一支股票一次),设计一个算法来计算你所能获取的最大利润。
注意:你不能在买入股票前卖出股票。
示例 1:
输入: [7,1,5,3,6,4]
输出: 5
解释: 在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 。
注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格。
思路:
只要记录前面的最小价格,将这个最小价格作为买入价格,然后将当前的价格作为售出价格,查看当前收益是不是最大收益。
//时间复杂度:O(n),只需要遍历一次。
//空间复杂度:O(1),只使用了常数个变量。
class Solution {
public:
int maxProfit(vector<int>& prices) {
if(prices.size()==0){return 0;}
int buy=prices[0];
int max_profits=0;
for(int i=1;i<prices.size();i++){
if(buy>prices[i]){
buy=prices[i];
}
else{
max_profits=max(max_profits,prices[i]-buy);
}
}
return max_profits;
}
};
6.股票买卖最佳时机II(122 easy)
给定一个数组,它的第 i 个元素是一支给定股票第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易(多次买卖一支股票)。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入: [7,1,5,3,6,4]
输出: 7
解释: 在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6-3 = 3
思路1:
对于 [a, b, c, d],如果有 a <= b <= c <= d ,那么最大收益为 d - a。而 d - a = (d - c) + (c - b) + (b - a) ,所以算法可以直接简化为只要今天比昨天大,就卖出。当访问到一个 prices[i] 且 prices[i] - prices[i-1] > 0,那么就把 prices[i] - prices[i-1] 添加到收益中。
//O(n) O(1)
class Solution {
public:
int maxProfit(vector<int>& prices) {
int profit=0;
for(int i=1;i<prices.size();i++){
if((prices[i]-prices[i])>0){
profit +=prices[i]-prices[i];
}
}
return profit;
}
};
思路2:
不断的找谷值和峰值,计算利润(注意不要错过一个峰值而去寻找下一个峰值,这样可能会损失一笔收益)
//JAVA代码 O(n) O(1)
class Solution {
public int maxProfit(int[] prices) {
int i = 0;
int valley = prices[0];
int peak = prices[0];
int maxprofit = 0;
while (i < prices.length - 1) {
while (i < prices.length - 1 && prices[i] >= prices[i + 1])
i++;
valley = prices[i];
while (i < prices.length - 1 && prices[i] <= prices[i + 1])
i++;
peak = prices[i];
maxprofit += peak - valley;
}
return maxprofit;
}
}
7.种花问题(easy 605)
思路1:
贪心思想,我们从左到右扫描数组 flowerbed,如果数组中有一个 0,并且这个 0 的左右两侧都是 0,那么我们就可以在这个位置种花,即将这个位置的 0 修改成 1,并将计数器 count 增加 1。对于数组的第一个和最后一个位置,我们只需要考虑一侧是否为 0。
class Solution {
public:
bool canPlaceFlowers(vector<int>& flowerbed, int n) {
if(n==0){return true;}
int count=0;
for(int i=0;i<flowerbed.size();i++){
if(flowerbed[i]==0 && (i==0 ||flowerbed[i-1] ==0)&& (i==flowerbed.size()-1 ||flowerbed[i+1]==0)){
flowerbed[i]=1;
count++;
}
}
return count>=n;
}
};
思路2:
在最左侧和左右侧分别加一个0,这样可以不用考虑边界问题,只要出现连续三个0,就可以在中间种一棵树
class Solution {
public:
bool canPlaceFlowers(vector<int>& flowerbed, int n) {
if(n==0){return true;}
flowerbed.insert(flowerbed.begin(),0);
flowerbed.insert(flowerbed.end(),0);
int count=0;
for(int i=1;i<flowerbed.size()-1;i++){
if(flowerbed[i-1]==0 && flowerbed[i]==0 && flowerbed[i+1]==0){
flowerbed[i]=1;
count++;
}
}
return count>=n;
}
};
知识点:c++创建m*n的二维空数组
1.vector<vector<int> >dp(m,vector<int>(n));//定义二维数组dp[][],m行 n列
2.int dp[m][n]
3.vector< vector<int> > array(5);
for (i = 0; i < array.size(); i++)
array[i].resize(3); //设置每行的个数大小 5行3列
vector<int> arr(10) //创建长度为10的一维数组
六、动态规划(dynamic planning)
递归和动态规划都是将原问题拆成多个子问题然后求解,他们之间最本质的区别是,动态规划保存了子问题的解,避免重复计算
重点是找状态转移方程
1.斐波那契数列
(1) 爬楼梯(easy 70)
题目描述:有 N 阶楼梯,每次可以上一阶或者两阶,求有多少种上楼梯的方法。
从第三个台阶开始,满足斐波那契数列
第 i 个楼梯可以从第 i-1 和 i-2 个楼梯再走一步到达,走到第 i 个楼梯的方法数为走到第 i-1 和第 i-2 个楼梯的方法数之和。
考虑到 dp[i] 只与 dp[i - 1] 和 dp[i - 2] 有关,因此可以只用两个变量来存储 dp[i - 1] 和 dp[i - 2],使得原来的 O(N) 空间复杂度优化为 O(1) 复杂度。
//时间复杂度:O(n),单循环到 n 。
//空间复杂度:O(n),dp 数组用了 n 的空间。
class Solution {
public:
int climbStairs(int n) {
if(n<=2){return n;}
int pre1=2,pre2=1;
for(int i=2;i<n;i++){
int curr=pre1+pre2; //状态转移方程
pre2=pre1;
pre1=curr;
}
return pre1;
}
};
(2)打家劫舍初级版(easy 198)
抢劫一排住户,但是不能抢邻近的住户,求最大抢劫量
示例 1:
输入: [1,2,3,1]
输出: 4
解释: 偷窃 1 号房屋 (金额 = 1) ,然后偷窃 3 号房屋 (金额 = 3)。
偷窃到的最高金额 = 1 + 3 = 4 。
由于不能抢劫邻近住户,如果抢劫了第 i -1 个住户,那么就不能再抢劫第 i 个住户,
所以:对于第i家有两种可能,抢劫,或保持先前状态
最大的金额 dp[i]=max(num[i]+dp[i-2], dp[i-1])
O(n) O(1)
class Solution {
public:
int rob(vector<int>& nums) {
int pre1=0,pre2=0;
for(int i=0;i<nums.size();i++){
int curr=max(nums[i]+pre2,pre1);
pre2=pre1;
pre1=curr;
}
return pre1;
}
};
(3)打家劫舍II(medium 213)
这个地方所有的房屋都围成一圈,这意味着第一个房屋和最后一个房屋是紧挨着的。同时,相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
偷从第一个到倒数第二个 或 第二个到最后一个 其中金额比较大的一个即可
class Solution {
public:
int rob(vector<int>& nums) {
if(nums.size()==0){return 0;}
if(nums.size()==1){return nums[0];}
int n=nums.size();
return max(rob(nums,0,n-2),rob(nums,1,n-1));
}
int rob(vector<int>& nums,int first,int last) {
int pre1=0,pre2=0;
for(int i=first;i<=last;i++){
int curr=max(nums[i]+pre2,pre1);
pre2=pre1;
pre1=curr;
}
return pre1;
}
};
(4)母牛生产
题目描述:假设农场中成熟的母牛每年都会生 1 头小母牛,并且永远不会死。第一年有 1 只小母牛,从第二年开始,母牛开始生小母牛。每只小母牛 3 年之后成熟又可以生小母牛。给定整数 N,求 N 年后牛的数量。
第 i 年成熟的牛的数量为:
dp[i]=dp[i-1]+dp[i-3]
2.矩阵路径问题
(1)最小路径(medium 64)
给定一个包含非负整数的 m x n 网格,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明:每次只能向下或者向右移动一步。
示例:
输入:
[
[1,3,1],
[1,5,1],
[4,2,1]
]
输出: 7
解释: 因为路径 1→3→1→1→1 的总和最小。
思路:动态规划
状态转移方程:dp[i][j]=dp[i][j]+min(dp[i-1][j],dp[i][j-1]
注意在最左侧和最上侧的情况,此时只有一种走法
O(m*n) O(1)
class Solution {
public:
int minPathSum(vector<vector<int>>& grid) {
if(grid.size() == 0 || grid[0].size() == 0) {return 0;}
int m=grid.size();
int n=grid[0].size();
for(int i=0;i<m;i++){
for(int j=0;j<n;j++){
if(i==0&&j==0){
grid[i][j]= grid[i][j];
}
else if(i==0){
grid[i][j]+=grid[i][j-1];
}
else if(j==0){
grid[i][j]+=grid[i-1][j];
}
else{
grid[i][j]+=min(grid[i-1][j],grid[i][j-1]);
}
}
}
return grid[m-1][n-1];
}
};
(2)不同路径(medium 62)
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为“Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为“Finish”)。
问总共有多少条不同的路径?
//O(mn) O(2N)
class Solution {
public:
int uniquePaths(int m, int n) {
//vector<vector<int> >grid(m,vector<int>(n));
int grid[m][n];
for(int i=0;i<m;i++){
for(int j=0;j<n;j++){
if(i==0 || j==0){
grid[i][j]=1;
}
else{
grid[i][j]=grid[i-1][j]+grid[i][j-1];
}
}
}
return grid[m-1][n-1];
}
};
//一次只记一行,当换行的时候数组里存放的是第i-1行的数据,本行的dp[j] = 上一行的dp[j] + 本行的dp[j-1], 所以dp[j] = dp[j] + dp[j-1].
public int uniquePaths(int m, int n) {
int[] dp = new int[n];
Arrays.fill(dp, 1);
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[j] = dp[j] + dp[j - 1];
}
}
return dp[n - 1];
}
3.数组区间类问题
(1)区间和检索-数组不可变(easy 303)
给定一个整数数组 nums,求出数组从索引 i 到 j (i ≤ j) 范围内元素的总和,包含 i, j 两点。
示例:
给定 nums = [-2, 0, 3, -5, 2, -1],求和函数为 sumRange()
sumRange(0, 2) -> 1
sumRange(2, 5) -> -1
sumRange(0, 5) -> -3
说明:
你可以假设数组不可变。
会多次调用 sumRange 方法。
因为要多次调用,所以没办法每次都求一次[i,j]的和,
求区间 i ~ j 的和,可以转换为 sum[j + 1] - sum[i],其中 sum[i] 为 0 ~ i-1的和。
//预计算时间O(n) 查询时间O(1) 空间O(n)
class NumArray {
private:
vector<int> sum;
public:
NumArray(vector<int>& nums) {
sum= vector<int>(nums.size()+1, 0);
for(int i=1;i<=nums.size();i++){
sum[i]=sum[i-1]+nums[i-1];
}
}
int sumRange(int i, int j) {
return sum[j+1]-sum[i];
}
};
/**
* Your NumArray object will be instantiated and called as such:
* NumArray* obj = new NumArray(nums);
* int param_1 = obj->sumRange(i,j);
*/
4.分割整数问题(太难理解了,之后再补充吧)
(1)整数拆分(medium 343)
给定一个正整数 n,将其拆分为至少两个正整数的和,并使这些整数的乘积最大化。 返回你可以获得的最大乘积。
输入: 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1
思路:动态规划
令dp[i]表示整数i对应的最大乘积,那么dp[i]的值应是dp[j](i-j),j属于[1,i-1]的最大值,同时注意dp[i]对应的值是经过拆分了的,所以还应判断两个数拆分的情况,即j(i-j)的值,取最大即可。
//O(n^2) O(n)
class Solution {
public:
int integerBreak(int n) {
vector<int> dp(n+1);
dp[1]=1;
dp[2]=1;
for(int i=3;i<=n;i++){
for(int j=1;j<=i-1;j++){
dp[i]=max(dp[i],max(j*(i-j),j*dp[i-j]));
}
}
return dp[n];
}
};
(2)完全平方和数
给定正整数 n,找到若干个完全平方数(比如 1, 4, 9, 16, …)使得它们的和等于 n。你需要让组成和的完全平方数的个数最少。
示例 1:
输入: n = 12
输出: 3
解释: 12 = 4 + 4 + 4.
思路:
对于数字n,可以进行分解,分解成某个数s和完全平方数的和,于是就有了
dp[n] = dp[s] + 1 。
然后我们假设(dp(n) )表示数字(n )最少可以表示为(dp(n) )个完全平方数的和,就能写出状态转移方程:
dp[i]=min(dp[i],dp[i-j*j]+1)
class Solution {
public:
int numSquares(int n) {
vector<int> dp(n+1);
dp[0]=0;
for(int i=1;i<=n;i++){
dp[i]=i;
for(int j=1;j*j<=i;j++){
dp[i]=min(dp[i],dp[i-j*j]+1);
}
}
return dp[n];
}
};
七.搜索算法
1.BFS
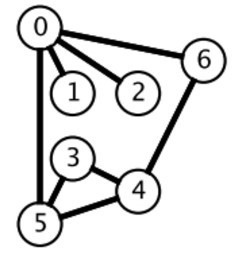
广度优先搜索一层一层地进行遍历,每层遍历都是以上一层遍历的结果作为起点,遍历一个距离能访问到的所有节点。需要注意的是,遍历过的节点不能再次被遍历
每一层遍历的节点都与根节点距离相同。设 di 表示第 i 个节点与根节点的距离,推导出一个结论:对于先遍历的节点 i 与后遍历的节点 j,有 di <= dj。利用这个结论,可以求解最短路径等 最优解 问题:第一次遍历到目的节点,其所经过的路径为最短路径。应该注意的是,使用 BFS 只能求解无权图的最短路径,无权图是指从一个节点到另一个节点的代价都记为 1。
在程序实现 BFS 时需要考虑以下问题:
队列:用来存储每一轮遍历得到的节点;
标记:对于遍历过的节点,应该将它标记,防止重复遍历。
代码模板如下:
void BFS()
{
定义队列;
定义备忘录,用于记录已经访问的位置;
判断边界条件,是否能直接返回结果的。
将起始位置加入到队列中,同时更新备忘录。
while (队列不为空) {
获取当前队列中的元素个数。
for (元素个数) {
取出一个位置节点。
判断是否到达终点位置。
获取它对应的下一个所有的节点。
条件判断,过滤掉不符合条件的位置。
新位置重新加入队列。
}
}
}
(1)二进制路径中的最短路径(1091 medium)
在一个 N × N 的方形网格中,每个单元格有两种状态:空(0)或者阻塞(1)。
一条从左上角到右下角、长度为 k 的畅通路径,由满足下述条件的单元格 C_1, C_2, …, C_k 组成:
相邻单元格 C_i 和 C_{i+1} 在八个方向之一上连通(此时,C_i 和 C_{i+1} 不同且共享边或角)
C_1 位于 (0, 0)(即,值为 grid[0][0])
C_k 位于 (N-1, N-1)(即,值为 grid[N-1][N-1])
如果 C_i 位于 (r, c),则 grid[r][c] 为空(即,grid[r][c] == 0)
返回这条从左上角到右下角的最短畅通路径的长度。如果不存在这样的路径,返回 -1 。

//O(n⋅sqrt(n) O(n)
),
class Solution {
public:
int shortestPathBinaryMatrix(vector<vector<int>>& grid) {
// breadth first search...
if (grid[0][0]) return -1;
const int N = grid.size();
const vector<vector<int>> DIRS = { // 顺时针的8个direction
{-1, 0}, {-1, 1}, {0, 1}, {1, 1}, {1, 0}, {1, -1}, {0, -1}, {1, -1}};
grid[0][0] = 2; // 标记为 visited ...
queue<pair<int, int>> q;
q.emplace(0, 0);
int ans = 1; // steps
while (!q.empty()) {
size_t size = q.size();
while (size--) {
int r = q.front().first, c = q.front().second;
q.pop();
if (r == N - 1 && c == N - 1) // 已经抵达右下角 ...
return ans;
for (auto& d : DIRS) {
int r1 = r + d[0], c1 = c + d[1];
if (r1 < 0 || c1 < 0 || r1 >= N || c1 >= N || grid[r1][c1])
continue;
grid[r1][c1] = 2; // visited ...
q.emplace(r1, c1);
}
}
ans++;
}
return -1;
}
};
(2)完全平方数(279 medium)
给定正整数 n,找到若干个完全平方数(比如 1, 4, 9, 16, …)使得它们的和等于 n。你需要让组成和的完全平方数的个数最少。
示例 1:
输入: n = 12
输出: 3
解释: 12 = 4 + 4 + 4.
思路一:BSF
可以一层一层的算。第一层依次减去一个平方数得到第二层,第二层依次减去一个平方数得到第三层。直到某一层出现了 0,此时的层数就是我们要找到平方数和的最小个数。
举个例子,n = 12,每层的话每个节点依次减 1, 4, 9…。如下图,灰色表示当前层重复的节点,不需要处理。
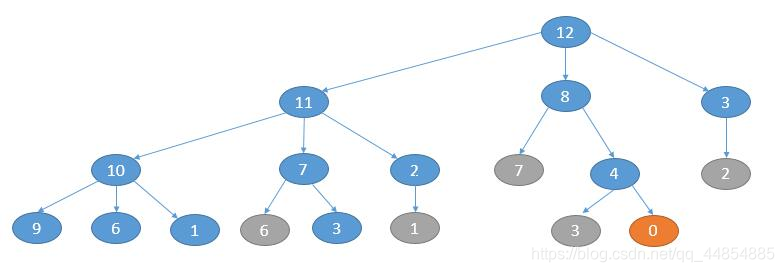
class Solution {
public:
int numSquares(int n) {
queue<int> q;
set<int> visit;
int path=0;
q.push(n);
while(!q.empty()){
int size=q.size();
path++; //每遍历完一层 path+1,先达到目标的层数就是最短路径
while(size-->0){ //一层一层遍历
int curr=q.front();
q.pop();
for(int i=1;i*i<=curr;i++){
int next=curr-i*i;
if(next==0){return path;}
if(visit.count(next)){continue;}
q.push(next);
visit.insert(next);
}
}
}
return n;
}
};
2.dfs
(1)岛屿的最大面积
给定一个包含了一些 0 和 1 的非空二维数组 grid 。
一个 岛屿 是由一些相邻的 1 (代表土地) 构成的组合,这里的「相邻」要求两个 1 必须在水平或者竖直方向上相邻。你可以假设 grid 的四个边缘都被 0(代表水)包围着。
找到给定的二维数组中最大的岛屿面积。(如果没有岛屿,则返回面积为 0 。)
示例 1:
[[0,0,1,0,0,0,0,1,0,0,0,0,0],
[0,0,0,0,0,0,0,1,1,1,0,0,0],
[0,1,1,0,1,0,0,0,0,0,0,0,0],
[0,1,0,0,1,1,0,0,1,0,1,0,0],
[0,1,0,0,1,1,0,0,1,1,1,0,0],
[0,0,0,0,0,0,0,0,0,0,1,0,0],
[0,0,0,0,0,0,0,1,1,1,0,0,0],
[0,0,0,0,0,0,0,1,1,0,0,0,0]]
对于上面这个给定矩阵应返回 6。注意答案不应该是 11 ,因为岛屿只能包含水平或垂直的四个方向的 1 。
思路:深度优先搜索
目的:知道网格中每个连通形状的面积,然后取最大值。
1.如果在一个土地上,以 4 个方向探索与之相连的每一个土地(以及与这些土地相连的土地),那么探索过的土地总数将是该连通形状的面积。
2.为了确保每个土地访问不超过一次,我们每次经过一块土地时,将这块土地的值置为 0。这样我们就不会多次访问同一土地。
//时间复杂度:O(R * C),其中 R 是给定网格中的行数,CC 是列数。我们访问每个网格最多一次。
//空间复杂度:O(R * C),递归的深度最大可能是整个网格的大小,因此最大可能使用 O(R * C) 的栈空间。
class Solution {
private:vector<vector<int>> direction={{1,0},{-1,0},{0,1},{0,-1}};
public:
int maxAreaOfIsland(vector<vector<int>>& grid) {
if(grid.size()==0 || grid[0].size()==0){return 0;}
int m=grid.size(),n=grid[0].size();
int maxarea=0;
for(int i=0;i<m;i++){
for(int j=0;j<n;j++){
maxarea=max(maxarea,grater(grid,i,j));
}
}
return maxarea;
}
int grater(vector<vector<int>>& grid,int i,int j){
int m=grid.size(),n=grid[0].size();
if(i<0 || i>=m || j<0||j>=n||grid[i][j]==0){//若超出边界或grid!=1,直接返回0
return 0;
}
grid[i][j]=0;//探索过的岛屿置零(沉岛)
int area=1;
for(auto d:direction){
area +=grater(grid,i+d[0],j+d[1]);
}
return area;
}
};
3.Backtracking(回溯)
Backtracking属于 DFS。
1.普通 DFS 主要用在 可达性问题 ,这种问题只需要执行到特点的位置然后返回即可。
2.而 Backtracking 主要用于求解 排列组合 问题,例如有 { ‘a’,‘b’,‘c’ } 三个字符,求解所有由这三个字符排列得到的字符串,这种问题在执行到特定的位置返回之后还会继续执行求解过程。
从全排列问题开始理解“回溯搜索”算法(深度优先遍历 + 状态重置 + 剪枝)
回溯算法详解
//回溯模板
for 选择 in 选择列表:
# 做选择
//将该选择从选择列表移除
路径.add(选择)
backtrack(路径, 选择列表)
# 撤销选择
路径.remove(选择)
(1) 电话号码的字母组合(medium 17)
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。

示例:
输入:“23”
输出:[“ad”, “ae”, “af”, “bd”, “be”, “bf”, “cd”, “ce”, “cf”].
思路:深度遍历,并记录每次组合的值,给res (回溯)
class Solution {
private:vector<string> table={"abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
public:
vector<string> letterCombinations(string digits) {
vector<string> res;
string str="";
dfs(res,digits,str,0);
return res;
}
void dfs(vector<string>& res,string& digits,string str,int i){
if(i>=digits.size()){
if(str.size()>0){
res.push_back(str);
}
return;
}
string s=table[digits[i]-'2'];
for(int j=0;j<s.size();j++){
str.push_back(s[j]);// 做选择
dfs(res,digits,str,i+1);
str.pop_back();//?////取消选择
}
}
};
(2)全排列(46 medium)
给定一个 没有重复 数字的序列,返回其所有可能的全排列。
示例:
输入: [1,2,3]
输出:
[
[1,2,3],
[1,3,2],
[2,1,3],
[2,3,1],
[3,1,2],
[3,2,1]
]
经典回溯问题
class Solution {
public:
vector<vector<int>> result;
vector<vector<int>> permute(vector<int>& nums) {
vector<int> track;
backtrack(nums, track);
return result;
}
void backtrack(vector<int> nums, vector<int> track) {
if(track.size() == nums.size()) {
result.push_back(track);
return;
}
int nums_size = nums.size();
for(int i = 0; i < nums_size; ++ i) {
//如果nums[i]没有出现在track中,即可供选择
if(find(track.begin(), track.end(), nums[i]) == track.end()) { //对于返回迭代器的查找,通过判断find(a.begin(),a.end(),value)==a.end(),来判断元素是否存在。如果不存在返回end(),所以判断value==a.end()
track.push_back(nums[i]);//做选择
backtrack(nums, track);//递归
track.pop_back();//取消选择
}
}
}
};
