作用有待更新....
大佬博客:https://www.cnblogs.com/jinkun113/p/4743694.html;
https://www.luogu.com.cn/problemnew/solution/P3809;
后缀数组:
复杂度:N(NlogN)
理论原理加模板:
后缀数组使用倍增法这里不加以叙述+桶排序;
先来了解一下桶排序,要拍一个1-99的数,我们先按照各位放到十个桶里,然后按照顺序取出来放到十位的桶里,这样我们在保证十位相同的时候个位小的先被放入桶里,所以答案的顺序就是对的,如图:
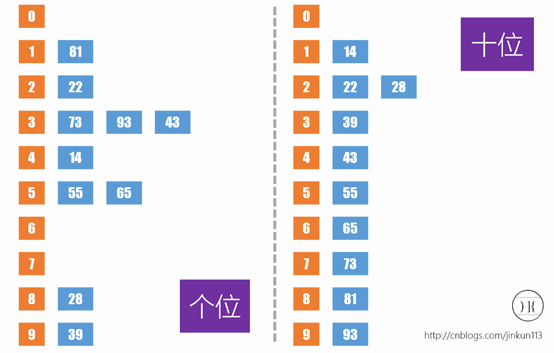
基于这个原理其实我们排序字符窜的时候也是先比较第一关键字是否相同然后判断第二关键字,所以我们在排序的时候,为了不多加一个桶,重复操作,我们可以按照第一关键字排序,然后按照第二关键字取出来,先被取出来的就是比较相同的一个排名区间里面比较小的,为什么是排名区间呢,我们桶排序时算出桶元素个数的前缀和,对于一个桶来说,他前面所拥有的元素都比他小,他后面桶的元素都比他大,所以我们知道的是一个区间,我们把元素小的先取出来附上排名,就可以确定这个区间的具体排名;
倍增:
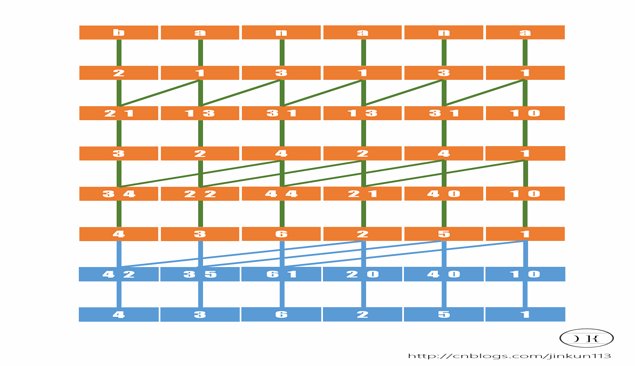
我们发现有些没有第二关键字,,就当作是0,放在最前面,有些排名做了别人的第二和关键字,位子随着循环次数是2的k次方的关系;
接下来看我们在更新第一关键字的时候就是rk,我们要判断两个排名是否相同就是第一和第二关键字是否相同,然后重新附上排名;看代码:
#include<iostream>
#include<cstdio>
using namespace std;
const int MAXN= ;
char s[MAXN];
int rk[MAXN],srk[MAXN],tax[MAXN],sa[MAXN],hi[MAXN];//rk第一关键字排名,srk第二关键字排名
int n,m=127;//'z'=126
void Rsort(int *rk,int *tp)
{
for(int i=1;i<=m;i++) tax[i]=0;//清空桶;
for(int i=1;i<=n;i++) tax[rk[i]]++;//按照第一关键字先放入不同的桶
for(int i=1;i<=m;i++) tax[i]+=tax[i-1];//要知道这个字符的排名就要先求出来他前面有多少个字符;
for(int i=1;i<=n;i++) sa[tax[rk[tp[i]]]--]=tp[i];//其实我们只要把桶中的每个元素取出来,他前面有多少数他的排名就是地基,只要按照第二个关键字把第一个关键字去出来
}
bool cmp(int r[],int a,int b,int k)
{
return r[a]==r[b]&&r[a+k]==r[b+k];
}
按照第一关键字放入不同的桶然后按照第二关键字把它取出来;完成基数排序;
void get_sa()
{
for(int i=1;i<=n;i++) rk[i]=a[i],tp[i]=i;
Rsort(rk,tp);
//因为我们要由2的k-1次到二的k次,那么需要找到下一个2的k-1次所在的位置的头位置,所以J代表我们要找的位置距离这个位置的距离
//循环桶排序
for(int j=1;j<n;j<<=1,m=p)//m=p的意思是我们看看这个排名最大到p所以只需要P个桶来排序
{
int p=0;
// 没有第二关键字,可以作为最小的0来处理
for(int i=1;i<=j;i++) srk[++p]=n-j+1;
// 然后我么根据平移的关系通过sa[i]遍历所有后缀的是否在可以作为其他字符的第二关键字
for(int i=1;i<=n;i++) if(sa[i]>j) srk[++p]=sa[i]-j;
Rsort(rk,srk);//按照第一关键字放入桶,按照第二关键字取出来
swap(rk,srk);//我们要更新rk,先把他放到第二关键字排序里面,因为如果第一关键字和第二关键字相同,则这两个字符窜相同
rk[sa[1]]=p=1;
for(int i=2;i<=n;i++)
rk[sa[i]]=comp(srk,sa[i],sa[i-1],j)?p:++p;//判断两个字符窜是否具有相同的排序
}
}
void gethi()
{
for (rint i=1;i<=n;++i) rk[sa[i]]=i;//使它没有重复排名
for(int i=1,j=0;i<=n;i++)
{
if(rk[i]==1) continue;//第一名的height=0
if(j) j--;
while(s[i+j]==s[sa[rk[i]-1]+j]) j++;
hi[rk[i]]=j;
}
}
int main()
{
scanf("%s",s+1);
n=strlen(s+1); 从第一个位置开始输入
get_sa();
}
作用用来O(N)求
最长公共前缀:LCA;
我们先看LCA的两条性质:
关于LCP的几条性质
显而易见的
- LCP(i,j)=LCP(j,i);
- LCP(i,i)=len(sa[i])=n-sa[i]+1;
这两条性质有什么用呢?对于i>j的情况,我们可以把它转化成i<j,对于i==j的情况,我们可以直接算长度,所以我们直接讨论i<j的情况就可以了。
我们每次依次比较字符肯定是不行的,单次复杂度为O(n),太高了,所以我们要做一定的预处理才行。
LCP Lemma
LCP(i,k)=min(LCP(i,j),LCP(j,k)) 对于任意1<=i<=j<=k<=n
证明:设p=min{LCP(i,j),LCP(j,k)},则有LCP(i,j)≥p,LCP(j,k)≥p。
设suff(sa[i])=u,suff(sa[j])=v,suff(sa[k])=w;
所以u和v的前p个字符相等,v和w的前p个字符相等
所以u和w的前p的字符相等,LCP(i,k)>=p
设LCP(i,k)=q>p 那么q>=p+1
因为p=min{LCP(i,j),LCP(j,k)},所以u[p+1]!=v[p+1] 或者 v[p+1]!=w[p+1]
但是u[p+1]=w[p+1] 这不就自相矛盾了吗
所以LCP(i,k)<=p
综上所述LCP(i,k)=p=min{LCP(i,j),LCP(j,k)}
LCP Theorem
LCP(i,k)=min(LCP(j,j-1)) 对于任意1<i<=j<=k<=n
这个结合LCP Lemma就很好理解了
我们可以把i~k拆成两部分i~(i+1)以及(i+1)~k
那么LCP(i,k)=min(LCP(i,i+1),LCP(i+1,k))
我们可以把(i+1)~k再拆,这样就像一个DP,正确性显然
怎么求LCP?
我们设height[i]为LCP(i,i-1),1<i<=n,显然height[1]=0;
由LCP Theorem可得,LCP(i,k)=min(height[j]) i+1<=j<=k
这里的i,j是sa中的顺序;这个很容易证明;把换元到sa数组
那么height怎么求,枚举吗?NONONO,我们要利用这些后缀之间的联系
设h[i]=height[rk[i]],同样的,height[i]=h[sa[i]];
那么现在来证明最关键的一条定理:
h[i]>=h[i-1]-1;
这个证明我觉得看上面第一个大佬的博客吧,我对代码进行一下简单的说明
证明过程来自曲神学长的blog,我做了一点改动方便初学者理解:
首先我们不妨设第i-1个字符串按排名来的前面的那个字符串是第k个字符串,注意k不一定是i-2,因为第k个字符串是按字典序排名来的i-1前面那个,并不是指在原字符串中位置在i-1前面的那个第i-2个字符串。
这时,依据height[]的定义,第k个字符串和第i-1个字符串的公共前缀自然是height[rk[i-1]],现在先讨论一下第k+1个字符串和第i个字符串的关系。
第一种情况,第k个字符串和第i-1个字符串的首字符不同,那么第k+1个字符串的排名既可能在i的前面,也可能在i的后面,但没有关系,因为height[rk[i-1]]就是0了呀,那么无论height[rk[i]]是多少都会有height[rk[i]]>=height[rk[i-1]]-1,也就是h[i]>=h[i-1]-1。
第二种情况,第k个字符串和第i-1个字符串的首字符相同,那么由于第k+1个字符串就是第k个字符串去掉首字符得到的,第i个字符串也是第i-1个字符串去掉首字符得到的,那么显然第k+1个字符串要排在第i个字符串前面。同时,第k个字符串和第i-1个字符串的最长公共前缀是height[rk[i-1]],
那么自然第k+1个字符串和第i个字符串的最长公共前缀就是height[rk[i-1]]-1。
到此为止,第二种情况的证明还没有完,我们可以试想一下,对于比第i个字符串的排名更靠前的那些字符串,谁和第i个字符串的相似度最高(这里说的相似度是指最长公共前缀的长度)?显然是排名紧邻第i个字符串的那个字符串了呀,即sa[rank[i]-1]。但是我们前面求得,有一个排在i前面的字符串k+1,LCP(rk[i],rk[k+1])=height[rk[i-1]]-1;
又因为height[rk[i]]=LCP(i,i-1)>=LCP(i,k+1)
所以height[rk[i]]>=height[rk[i-1]]-1,也即h[i]>=h[i-1]-1。
void gethi()
{
for (rint i=1;i<=n;++i) rk[sa[i]]=i;//使它没有重复排名
for(int i=1,j=0;i<=n;i++)
{
if(rk[i]==1) continue;//第一名的height=0
if(j) j--;//j只要减1,然后继续去匹配
while(s[i+j]==s[sa[rk[i]-1]+j]) j++;//这一部就是求第i个字符窜在sa中和他前面一个匹配;
hi[rk[i]]=j;
}
}