回归(Regression)算法指标
以下为一元变量和二元变量的线性回归示意图:
怎样来衡量回归模型的好坏呢?
我们自然而然会想到采用残差(实际值 \(y_i\) 与预测值 \(\hat y_i\) 差值)的均值来衡量,即:
\[ \text {residual}(y,\hat y_i)=\frac {1}{m} \sum_{i=1}^m(y_i- {\hat y_i}) \]
问题①:用残差的均值合理吗?
平均绝对误差 Mean Absolute Error
用残差的均值不合理,这样容易正负残差抵消。
平均绝对误差 MAE(Mean Absolute Error)又被称为 \(l1\) 范数损失(\(l1-normloss\))
\[ \text {MAE}(y,\hat y_i) = \frac {1}{m} \sum_{i=1}^n |y- {\hat y_i}| \]
问题②:MAE 有哪些不足?
均方误差 Mean Squared Error
MAE 绝对值函数不光滑,这不利于求导。
均方误差 MSE(Mean Squared Error)又被称为 \(l2\) 范数损失(\(l2-normloss\))
\[ \text {MSE}(y,\hat y_i) = \frac {1}{m} \sum_{i=1}^n (y-{\hat y_i})^2 \]
问题③:还有没有比 MSE 更合理的指标?
均方根误差 Root Mean Squared Error
回想一下方差和标准差的定义,可以试图让评估指标与参数的单位一致。
\[ \text {RMSE}(y,\hat y_i) = \sqrt {\frac {1}{m} \sum_{i=1}^n (y- {\hat y_i})^2} \]
问题④:有没有规范化(无量纲化)的指标?
决定系数 Coefficient of Determination
这就好像假设上海的房价均方根误差为 1000 ,这可以接受,可如果四五线城市是这个价格...所以需要把值归到 0 和 1 之间,以免对不同的场景和模型。
决定系数又称为 \(R^2 score\) ,反映因变量的全部变异能通过回归关系被自变量解释的比例。变异和方差有点类似,方差反映实际值均值 \(\overline y\) 附近样本点离散的程度,而实际值 \(y\) 的变异是方差的 \(m\) 倍,也就是下面的总离差平方和 SST :
\[ \text{SST} = \sum_i^m(y_i-\overline y)^2 \quad \text {SST=total sum of squares} \]
而回归平方和 SSR 是预测值的变异:
\[ \text{SSR} = \sum_i^m(\hat y_i-\overline y)^2 \quad \text {SSR=sum of due to regression} \]
残差平方和 SSE 表示实际值与预测值之间的差异:
\[ \text{SSE} = \sum_i^m(\hat y_i-y_i)^2 \quad \text {SSE=sum of due to errors} \]
你会发现 \(\text{SSE+SSR=SST }\) ,这个可以通过最小二乘法原理进行证明:
\[ y-\overline y=(y-\hat y)+(\hat y-\overline y) \\ \Rightarrow \sum (y-\overline y)^2 = \sum (y-\hat y)^2+\sum(\hat y-\overline y)^2+2\sum (y-\hat y)(\hat y-\overline y) \\ \begin {align*} \because \sum (y-\hat y)(\hat y-\overline y) &= \sum (y-\hat y)(a+bx-\overline y) \\ &= \sum (y-\hat y)[(a-\overline y) +bx] \\ &= (a-\overline y) \sum (y-\hat y)+b \sum (y-\hat y)x \\ &= (a-\overline y) \sum (y-a-bx)+b \sum (y-a-bx)x \end {align*} \]
根据最小二乘法原理,有:
\[ \sum (y-a-bx) = 0,\sum (y-a-bx)x=0 \\ \therefore \sum (y-\hat y)(\hat y-\overline y) = 0 \\ \therefore \sum (y-\overline y)^2 = \sum (y-\hat y)^2+\sum(\hat y-\overline y)^2 \]
证明出 \(\text{SSE+SSR=SST }\) 后,我们定义 \(R^2(y,\hat y)=\frac {\text{SSR}}{\text{SST}}\) ,就能够反映模型的预测能力。如果结果是 0,就说明模型预测不能预测因变量;如果结果是 1,就说明是函数关系。如果结果在 0 - 1 之间,就能表示模型的好坏程度,不受使用场景的影响。
化简上面的公式,分子就变成了均方误差 MSE,分母就变成了方差:
\[ \begin {align*} R^2(y,\hat y) &=\frac {\text{SSR}}{\text{SST}} = 1- \frac {\text{SSE}}{\text{SST}} \\ & = 1 - \frac { \sum_i^m(\hat y_i-y_i)^2 }{ \sum_i^m( y_i-\overline y)^2 } \\ & = 1 - \frac { \sum_i^m(\hat y_i-y_i)^2 /m}{ \sum_i^m( y_i-\overline y)^2/m } \\ & = 1 - \frac {\text{MSE}(\hat y,y)} {\text {Var}(y)} \end {align*} \]
在实际工作当中不会使用单个指标,而是权衡多个指标。
分类(Classification)算法指标
精度 Accuracy
预测正确的样本占总样本的比例,取值范围为 \([0,1]\) , 取值越大,模型预测能力越好。
\[ Acc(y,\hat y) = \frac {1}{m} \sum_{i=1}^m sign(\hat y_i,y_i) \]
其中 $sign(\hat y_i,y_i) = \begin{cases}1 \quad \hat y_i=y_i \ 0 \quad \hat y_i \neq y_i\end{cases} $
问题⑤: 什么时候精度指标会失效?
混淆矩阵 Confusion Matirx
混淆矩阵,在无监督学习中被称为匹配矩阵(matching matrix),之所以叫混淆矩阵,是因为我们能很容易地从图中看出学习器有没有将样本的类别给搞混淆。矩阵每一列表示分类器的预测,每一行表示样本所属的真实类别。如下图所示:
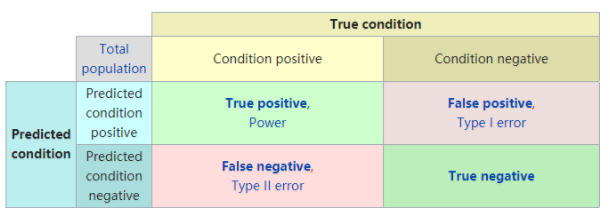
混淆矩阵维基百科:https://en.wikipedia.org/wiki/Confusion_matrix
这里牵扯到三个方面:真实值、预测值、预测值和真实值之间的关系,已知其中任意两个都可以求出第三个部分,通常取 预测值和真实值之间的关系 、预测值 对矩阵进行划分:
- True positive(TP)
真实值为 Positive,预测正确(预测值为 Positive)
- True negative(TN)
真实值为 Negative,预测正确(预测值为 Negative)
- False positive(FP)
真实值为 Negative,预测错误(预测值为 Positive),Type I error
- False negative(FN)
真实值为 Positive,预测错误(预测值为 Negative),Type II error
混淆矩阵的衍生指标:

实际上常用的就那么几个,有兴趣的可以自己了解其它的指标。
准确率(查准率) Precision
Precision 是分类器预测的正样本中预测正确的比例:
\[ \text{Precision}=\frac {\sum\text{True positive}}{\sum \text{Predicted condition positive}}= \frac {\text{TP}}{\text{TP+FP}} \]
召回率(查全率) Recall
Recall 是分类器识别出的正样本占所有正样本的比例:
\[ \text{Recall}=\frac {\sum\text{True positive}}{\sum \text{Condition positive}}= \frac {\text{TP}}{\text{TP+FN}} \]
\(F_1\) Score 和 \(F_\beta\) Score
Precision 和 Recall 是互相影响的,理想情况下很难做到两者值都很高,为了均衡两个指标,常常会使用他们的调和平均值 \(F_1\) Score:
\[ F_1=\frac {2}{\frac {1}{\text {recal}l}+\frac {1}{\text {precision}}} = 2 \frac {\text{precision}\cdot \text{recall}}{\text{precision } + \text{recall}} \]
更一般的情况下使用的是加权调和平均值 \(F_\beta\) Score:
\[ F_\beta=(1+\beta ^2)\frac {\text{precision}\cdot \text{recall}}{\beta ^2 \times \text{precision } + \text{recall}} \]
其中 \(\beta\) 表示权重,同样地可以表示为:
\[ F_\beta=\frac {1}{\frac {\beta^2}{(1+\beta^2) \times\text {recal}l}+\frac {1}{(1+\beta^2) \times\text {precision}}} \\ = \frac {1}{\frac {1}{(1+\frac {1} {\beta^2}) \times\text {recal}l}+\frac {1}{(1+\beta^2) \times\text {precision}}} \]
当 $\beta \to 0 $, \(F_\beta \approx P\) ;当 \(\beta \to \infty\) ,\(F_\beta \approx R\) ; \(\beta\) 取 \(1\) 时即为 \(F_1\) Score.
问题⑥:有没有不依赖于阈值的指标?