数据结构和算法之时间空间复杂度（上）

一、为什么需要复杂度分析？

我们不进行复杂度分析，而是把代码跑一遍，通过统计、监控就能得到算法执行时间和占用的内存大小，为什么还要做时间、空间复杂度分析呢？我将这种分析称之为事后统计法。

二、事后统计法问题

• 首先确认事后统计法确实没问题，可以很好的统计出算法的运行时间占比以及所占用的内存大小。但是存在如下两个问题：
• 测试结果非常依赖测试环境

测试环境硬件不同会对测试结果有很大影响，比如我们拿i9处理器和i3处理器来运行，两个事后统计法出来的结果差别是很大的。

• 测试结果受数据规模的影响很大

比如排序算法，待排序数据的有序度不一样，排序的执行时间就会有很大的差别，极端情况下，若数据都是有序的，那排序算法不需要做任何操作，时间会很短，若待排序的数据都是无序的，那么算法执行时间会很长。

• 综上两点：事后统计法是存在问题的，我们需要一个不用具体的测试数据来测试，就可以粗略的估算出算法的执行效率的方法。这就是此篇的时间、空间复杂度分析法。

三、大O复杂度表示法

1、实战分析

1.1、实战一

1 private int cal (int n) {
2	int sum = 0;
3	for (int i = 1; i <= n; i ++) {
4		sum += i;
5	}
6	return sum;
7 }

含义：求1，2，3，…n的累加和。

1.2、分析一

假设每一行代码执行的时间都是1个unit_time，那么如上程序可以拆解为如下：
第2行执行时间为1个unit_time，第3，4行执行时间分别为n个unit_time，也就是2n个unit_time，所以上个cal方法所需要的全部执行时间T(n)为(1+2n)unit_time。

1.3、实战二

1 private int cal (int n) {
2 	int sum = 0;
3	int i = 1;
4	int j = 1;
5	for (; i <= n; i ++) {
6		j = 1;
7		for (; j <= n; j ++) {
8			sum = sum + i * j;
9		}
10	 }
11 }

1.4、分析二

按照上面分析一的套路来分析这个案例二。第2，3，4行时间占比总和=3个unit_time，第5，6行占比2n个time_unit，第7，8行占比2n²unit_time（为什么是2n²，因为他外层还有一层for循环，这里为双层for，会执行n²遍，由于7，8是两行，所以2n²）。所以上面程序的总执行时间T(n) = (2n² + 2n + 3)unit_time。

1.5、实战总结

所有代码的执行时间T(n)与每行代码的执行次数n成正比。总结成公式如下：
T(n) = O(f(n))

公式解释
T(n)：代码执行的时间
n：数据规模大小
f(n)：每行代码执行的次数总和
O：表示代码的执行时间T(n)与f(n)表达式成正比
所以案例一：T(n) = O(1 + 2n)，案例二：T(n) = O(2n² + 2n + 3)，这就是著名的大O时间复杂度表示法。

2、三大忽略

2.1、忽略常数项

2.1.1、图解

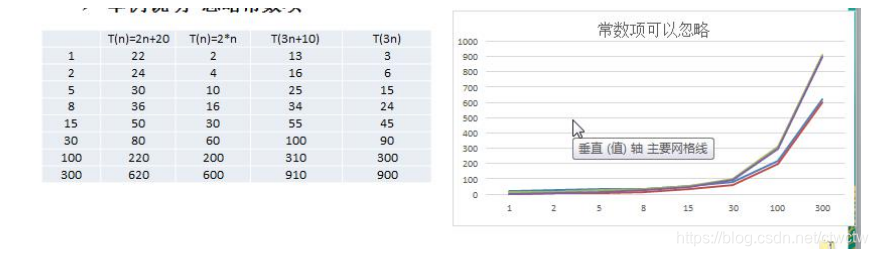
2.1.2、结论

• 2n+20和2n随着n变大，执行曲线无限接近，20可以忽略不记。
• 3n+10和3n随着n变大，执行曲线无限接近，10可以忽略不记。

2.2、忽略低次项（低阶）

2.2.1、图解

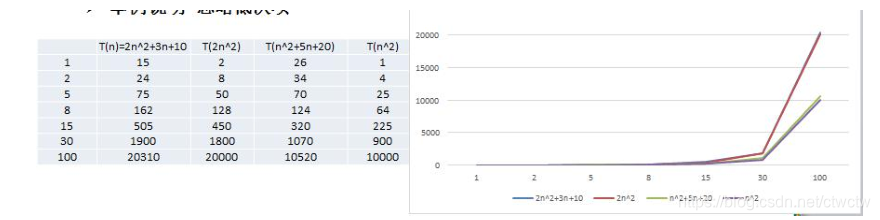
2.2.2、结论

• 2n²+3n+10和2n²随着n变大，执行曲线无限接近，可以忽略3n+10
• n²+5n+20和n²随着n变大，执行曲线无限接近，可以忽略5n+20

2.3、忽略系数

2.3.1、图解

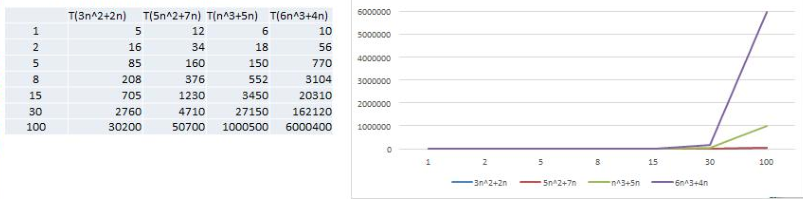
2.3.2、结论

• 随着n变大，5n²+7n和3n²+2n，执行曲线重合，说明这种情况下，系数5和3可以忽略。
• n³+5n和6n³+4n，执行曲线分离，说明多少次方是关键，和系数关系不大。

2.4、实战

上述实战一和实战二的时间复杂度按照如上三点忽略，就可以记为：T(n)=O(n)和T(n)=O(n²)

3、如何进行时间复杂度分析

3.1、只关注循环执行次数最多的一段代码

3.1.1、实战

1 private int cal (int n) {
2	int sum = 0;
3	int i = 1;
4	for (; i <= n; ++i) {
5		sum += i;
6	}
7	return sum;
8 }

3.1.2、分析

按照上面的套路那就是T(n)=O(2+2n)，再按照三大忽略的套路那就是T(n)=O(n)。
其实也可以按照只关注循环执行次数最多的一段代码这个法则来，那就是直接舍弃23行，直接奔入主题45两行，2n的复杂度，忽略系数记为O(n)。

3.2、加法法则：总复杂度等于量级最大的那段代码的复杂度

3.2.1、实战

private int cal (int n) {
	int sum1 = 0;
	int i = 1;
	for (; i < 100; i ++) {
		sum1 += i;
	}
	int sum2 = 0;
	int j = 1;
	for (; j < n; j ++) {
		sum2 += j;
	}
	int sum3 = 0;
	int m = 1;
	int p = 1;
	for (; m <= n; m ++) {
		p = 1;
		for (; p <= n; p ++) {
			sum3 = sum3 + m * p;
		}
	}
	return sum1 + sum2 + sum3;
}

3.2.2、分析

将上述代码分为三部分：分别求sum1、sum2和sum3。我们分别分析这三块的时间复杂度，然后找到最大的时间复杂度作为本段代码的最终结果。
1.第一段：T(n)=O(100)，忽略常数，则此段为O(1)
2.第二段：T(n)=O(n)
3.第三段：T(n)=O(n²)
所以整段代码的时间复杂度为O(n²)

3.3、乘法法则：嵌套代码的复杂度等于嵌套内外代码复杂度的乘积

3.3.1、实战

private int cal (int n) {
	int ret = 0;
	int i = 1;
	for (; i < n; i ++) {
		ret = ret + f(i);
	}
}
private int f (int n) {
	int sum = 0;
	int i = 1;
	for (; i < n; i ++) {
		sum += i;
	}
	return sum;
}

3.3.2、分析

第一个函数T1(n)=O(n)，第二个函数T2(n)=O(n)，因为第一个函数for里面调用第二个函数，所以整个cal函数的时间复杂度T(n)=T1(n)*T2(n)=O(n×n)=O(n²)

4、几种常见的时间复杂度

4.1、常量阶O(1)

4.1.1、描述

只要代码的执行时间不随n的增大而增长，这样代码的时间复杂度我们都记作O(1)。或者说，一般情况下，只要算法中不存在循环语句（若存在循环，且循环次数是固定已知的，那也是O(1)）、递归语句、即使有成千上万行的代码，其时间复杂度也是O(1)。

4.1.2、实战

int i = 8;
int j = 9;
int sum = i + j;
for (int n = 0; n < 10000; n ++) {
	sum += n;
}

不管你写多少代码，只要代码的执行时间不随 n 的增大而增长，这样代码的时间复杂度我们都记作 O(1)。

4.2、对数阶O(log₂n)

4.2.1、描述

对数阶，简单来讲就是2^x=n，不管底数是几，一般都称之为logn。最典型的案例就是二分查找法。

4.2.2、实战

int i = 1;
while (i <= n) {
	i = i * 2;
}

变量i的值从1开始，每次循环i都乘以2，当i>n的时候跳出循环，注意这里并不是每次i++，而是每次循环i*2，所以变量i的值其实就是一个等比数列，如下：
2⁰ 2¹ 2² 2³…2^x = n，所以2^x = n，x=log₂n，所以这段代码的时间复杂度就是O(log₂n)

4.3、线性阶O(n)

4.3.1、描述

只要代码的执行时间随n的增大而增长，这样代码的时间复杂度我们都记作O(n)。

4.3.2、实战

for (int i = 0; i < n; i ++) {
	// do somethings ...
}

类似这种n是未知数，n越大，这段代码执行时间越久的情况都称之为O(n)

4.4、线性对数阶O(nlog₂n)

4.2.1、描述

不管底数是几，一般都称之为nlogn。就是将对数阶（logn）外面套层循环(循环次数为n)。

4.2.2、实战

for (int m = 1; m < n; m ++) {
	int i = 1;
	while (i <= n) {
		i = i * 2;
	}
}

4.5、平方阶O(n²)

4.5.1、描述

O(n)的平方。换句话说就是双层嵌套for n。

4.5.2、实战

for (int x = 1; x <= n; x ++) {
	for (int i = 0; i < n; i ++) {
		// do somethings ...
	}
}

第一层for的T1(n)=O(n)，第二层for的T2(n)=O(n)，这段程序是嵌套for，所以T(n)=T1(n)*T2(n)=O(n×n)=O(n²)

4.6、立方阶O(n³)

同平方阶O(n²)，只是换成立方。说直接点就是三层嵌套for n。

4.7、K次方阶O(n^k)

平方阶O(n²)，只是换成n的k次方。。说直接点就是k层嵌套for n。

4.8、指数阶O(2ⁿ)和阶乘阶O(n!)

这两种比较特殊，属于非多项式量级。也就是说当数据规模n越来越大的时候，非多项式量级算法的执行时间会急剧增长，求解问题的执行时间会无限增长。效率贼低的算法，程序中必须避免。

5、时间复杂度的由小到大排序

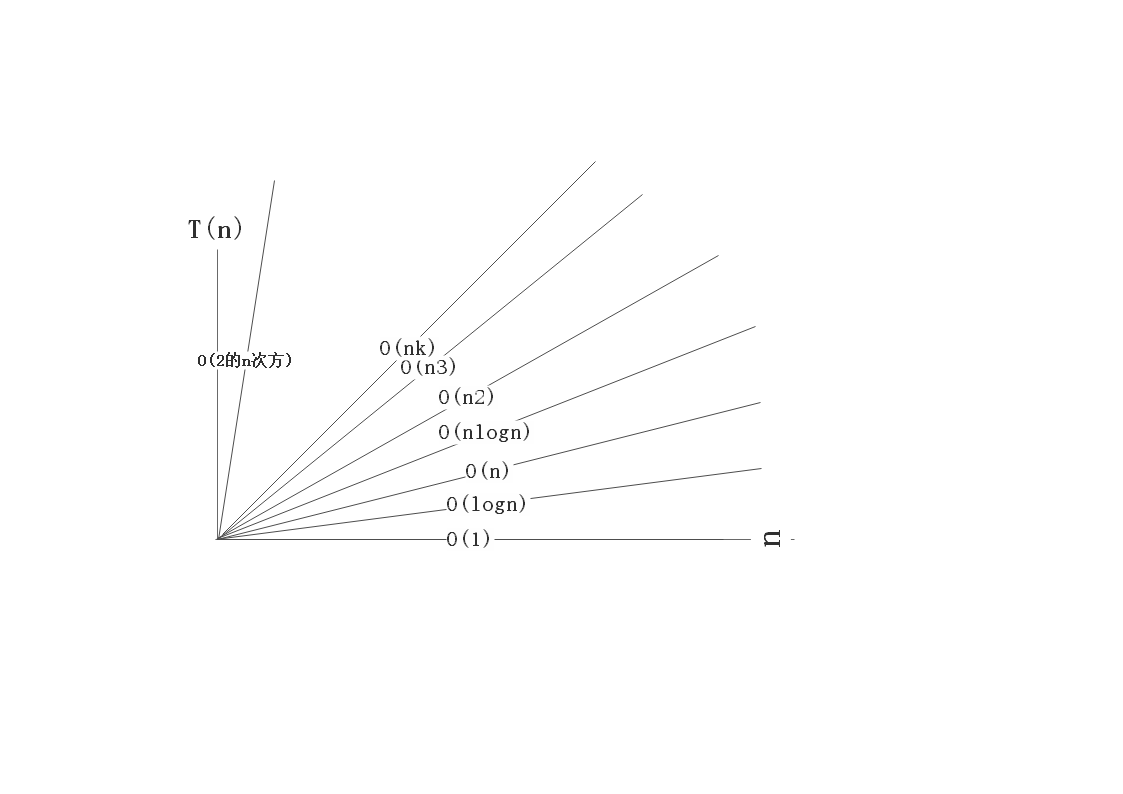
从低阶到高阶排序：O(1) < O(logn) < O(n) < O(nlogn) < O(n²) < O(n³) < O(n^k) < O(2_n) < O(n!)

四、空间复杂度

1、简介

表示算法的存储空间与数据规模之间的增长关系。

2、实战

1 private void test(int n) {
2	int i = 0;
3	int[] arr = new int[n];
4	for (i; i < n; i ++) {
5		a[i] = i * i;
6	}
}

分析：
第2行，申请了一个空间存储变量i，但是他是常量阶的，和n无关。所以为O(1)，第3行申请了一个大小为n的int类型数组，所以为O(n)，所以我们的口诀，加法法则：总复杂度等于量级最大的那段代码的复杂度。所以此段代码空间复杂度为O(n)。
空间复杂度常见的只有：O(1)、O(n)、O(n²)三个。