回溯算法团灭子集、排列、组合问题
一、子集
给定一组不含重复元素的整数数组 nums,返回该数组所有可能的子集(幂集)。
说明:解集不能包含重复的子集。
示例:
输入: nums = [1,2,3]
输出:
[
[3],
[1],
[2],
[1,2,3],
[1,3],
[2,3],
[1,2],
[]
]
第一个解法是利用数学归纳的思想:假设我现在知道了规模更小的子问题的结果,如何推导出当前问题的结果呢?
具体来说就是,现在让你求 [1,2,3] 的子集,如果你知道了 [1,2] 的子集,是否可以推导出 [1,2,3] 的子集呢?先把 [1,2] 的子集写出来瞅瞅:
[ [],[1],[2],[1,2] ]
你会发现这样一个规律:
subset([1,2,3]) - subset([1,2])
= [3],[1,3],[2,3],[1,2,3]
而这个结果,就是把 sebset([1,2]) 的结果中每个集合再添加上 3。换句话说,如果 A = subset([1,2]) ,那么:
subset([1,2,3])
= A + [A[i].add(3) for i = 1..len(A)]
这就是一个典型的递归结构嘛,[1,2,3] 的子集可以由 [1,2] 追加得出,[1,2] 的子集可以由 [1] 追加得出,base case 显然就是当输入集合为空集时,输出子集也就是一个空集。
翻译成代码就很容易理解了:
vector<vector<int>> subsets(vector<int>& nums) {
// base case,返回一个空集
if (nums.empty())
return {{}};
// 把最后一个元素拿出来
int n = nums.back();
nums.pop_back();
// 先递归算出前面元素的所有子集
vector<vector<int>> res = subsets(nums);
int size = res.size();
for (int i = 0; i < size; i++)
{
// 然后在之前的结果之上追加
res.push_back(res[i]);
//在每个结果后面push一个前面保存的元素n
res.back().push_back(n);
//eg:{1,2} : {},{1},{2},{1,2}
//n = 2 res = subsets()
// n = 1 res = sunsets()
// res = { {} }
// i = 0; i < 1;i ++
// res = { {}, {} }
// res = { {},{1} }
//i = 0;i < 2;i ++
//res = { {},{1},{} }
//res = { {},{1},{2} }
//res = { {},{1},{2},{1} }
//res = { {},{1},{2},{1,2} }
}
return res;
}
这个问题的时间复杂度计算比较容易坑人。我们之前说的计算递归算法时间复杂度的方法,是找到递归深度,然后乘以每次递归中迭代的次数。对于这个问题,递归深度显然是
,但我们发现每次递归 for 循环的迭代次数取决于 res 的长度,并不是固定的
根据刚才的思路,res 的长度应该是每次递归都翻倍,所以说总的迭代次数应该是 。或者不用这么麻烦,你想想一个大小为 N 的集合的子集总共有几个? 个对吧,所以说至少要对 res 添加 次元素.
那么算法的时间复杂度就是 吗?还是不对, 个子集是 push_back 添加进 res 的,所以要考虑 push_back 这个操作的效率:
for (int i = 0; i < size; i++) {
res.push_back(res[i]); // O(N)
res.back().push_back(n); // O(1)
}
因为 res[i] 也是一个数组呀,push_back 是把 res[i] copy 一份然后添加到数组的最后,所以一次操作的时间是 。
综上,总的时间复杂度就是 ,还是比较耗时的。
空间复杂度的话,如果不计算储存返回结果所用的空间的,只需要 的递归堆栈空间。如果计算 res 所需的空间,应该是 。
第二种通用方法就是回溯算法。而回溯算法的模板:
result = []
def backtrack(路径, 选择列表):
if 满足结束条件:
result.add(路径)
return
for 选择 in 选择列表:
做选择
backtrack(路径, 选择列表)
撤销选择
只要改造回溯算法的模板就行了
vector<vector<int>> res;
vector<vector<int>> subsets(vector<int>& nums) {
// 记录走过的路径
vector<int> track;
backtrack(nums, 0, track);
return res;
}
void backtrack(vector<int>& nums, int start, vector<int>& track) {
res.push_back(track);
for (int i = start; i < nums.size(); i++) {
// 做选择
track.push_back(nums[i]);
// 回溯
backtrack(nums, i + 1, track);
// 撤销选择
track.pop_back();
}
}
//eg : {1,2}
//backtrack(nums,0,track);
//res : { {} } i = 0;i < 2;i++
//track : {1};
// backtrack(i + 1)
// res = { {},{1}},i = 1;i < 2;i++
// track : { {1,2} };
// backtrack(nums,i + 1,track)
// res : {{},{1},{1,2}};i = 2;i < 2;i++ return;
// track : {1} return;
//track : { {} }
//track : { {2} };
// backtrack(i + 1);
// res : {{},{1},{1,2},{2}};i = 2;i < 2;i++;return
//track : { {} };
//return
不要看他比较复杂,但是其本身就是比较复杂,但是千万不要用脑袋去’递归‘,要记住框架逻辑再举个简单的例子即可
可以看见,对 res 更新的位置处在前序遍历,也就是说,res 就是树上的所有节点(所以代码中没有对结果进行if判断):
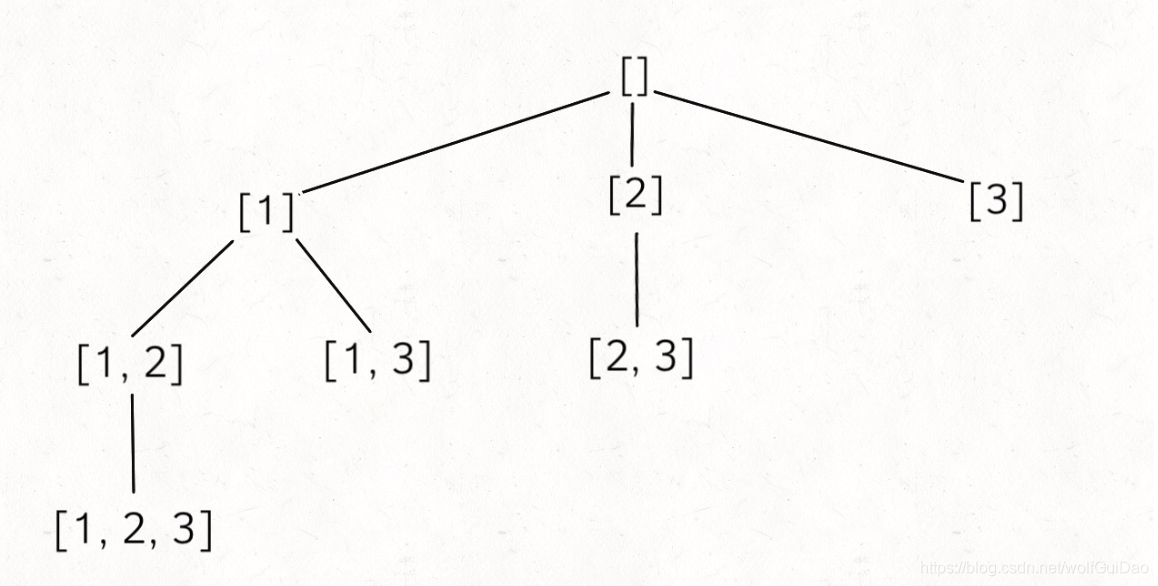
二、组合
给定两个整数 n 和 k,返回 1 … n 中所有可能的 k 个数的组合(不能重复)。
示例:
输入: n = 4, k = 2
输出:
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]
这也是典型的回溯算法,k 限制了树的高度,n 限制了树的宽度,继续套我们以前讲过的回溯算法模板框架就行了:
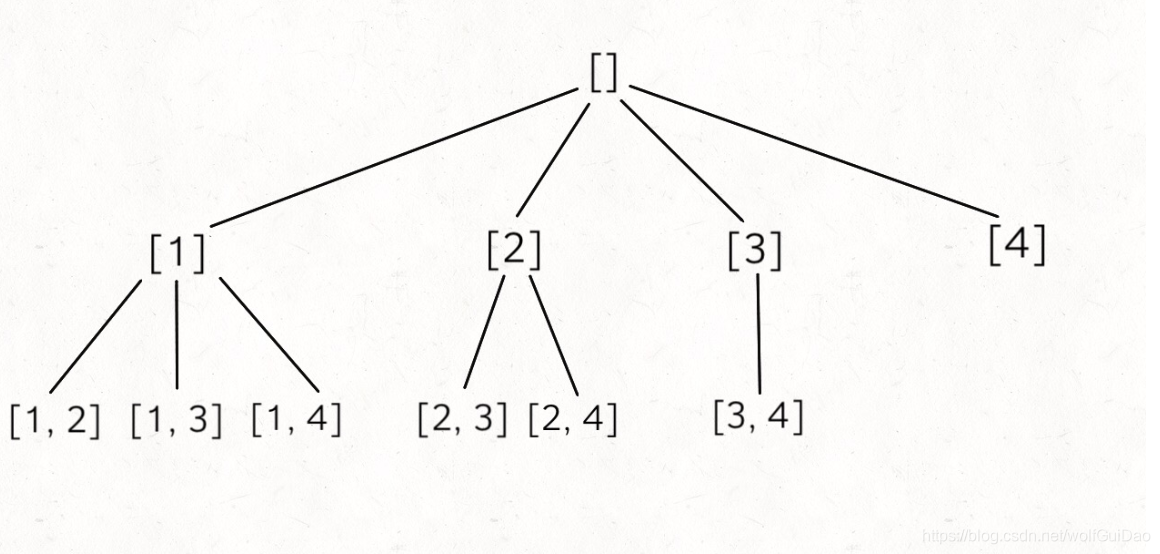
vector<vector<int>>res;
vector<vector<int>> combine(int n, int k) {
if (k <= 0 || n <= 0)
return res;
vector<int> track;
backtrack(n, k, 1, track);
return res;
}
void backtrack(int n, int k, int start, vector<int>& track) {
// 到达树的底部
if (k == track.size())
{
res.push_back(track);
return;
}
// 注意 i 从 start 开始递增
for (int i = start; i <= n; i++) {
// 做选择
track.push_back(i);
backtrack(n, k, i + 1, track);
// 撤销选择
track.pop_back();
}
}
backtrack 函数和计算子集的差不多,区别在于,更新 res 的时机是树到达底端时。
三、排列
给定一个没有重复数字的序列,返回其所有可能的全排列。
示例:
输入: [1,2,3]
输出:
[
[1,2,3],
[1,3,2],
[2,1,3],
[2,3,1],
[3,1,2],
[3,2,1]
]
首先画出回溯树来看一看:
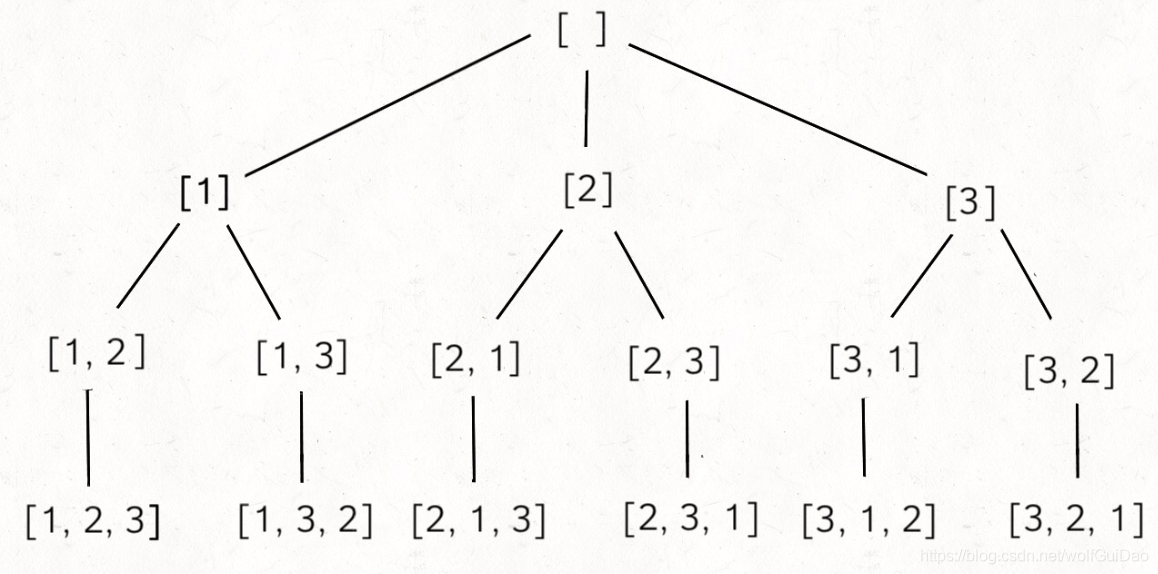
java代码:
List<List<Integer>> res = new LinkedList<>();
/* 主函数,输入一组不重复的数字,返回它们的全排列 */
List<List<Integer>> permute(int[] nums) {
// 记录「路径」
LinkedList<Integer> track = new LinkedList<>();
backtrack(nums, track);
return res;
}
void backtrack(int[] nums, LinkedList<Integer> track) {
// 触发结束条件
if (track.size() == nums.length) {
res.add(new LinkedList(track));
return;
}
for (int i = 0; i < nums.length; i++) {
// 排除不合法的选择
if (track.contains(nums[i]))
continue;
// 做选择
track.add(nums[i]);
// 进入下一层决策树
backtrack(nums, track);
// 取消选择
track.removeLast();
}
}
C++代码:
class Solution {
public:
vector<vector<int>> ret;//保存最后的结果
vector<vector<int>> permute(vector<int>& nums) {
if(nums.empty())
{
return ret;
}
vector<int> track;//保存单次结果
backtrack(nums,track);//递归
return ret;
}
void backtrack(vector<int>& nums,vector<int>& track)
{
if(track.size() == nums.size())//当track中的元素和nums中的元素个数相等
//时,代表是一种全排列,可以放到ret的结果中
{
ret.push_back(track);
return;
}
//循环回朔
for(int i = 0;i < nums.size();i++)
{
//如果nums[i]这个元素已经存在track中,代表上次的选择错误,
//continue回去,判断下一个元素
//反之,就把nums这个元素直接放到track中,继续回朔判断
if(IsExist(track,nums[i]))
{
track.push_back(nums[i]);
}
else
{
continue;
}
backtrack(nums,track);
//撤销选择
track.pop_back();
}
}
//在track中判断一个元素是否已经存在
bool IsExist(vector<int>& track,int val)
{
for(auto e : track)
{
if(e == val)
{
return false;
}
}
return true;
}
};
回溯模板依然没有变,但是根据排列问题和组合问题画出的树来看,排列问题的树比较对称,而组合问题的树越靠右节点越少。
在代码中的体现就是,排列问题每次通过 contains 方法来排除在 track 中已经选择过的数字;而组合问题通过传入一个 start 参数,来排除 start 索引之前的数字。
注意对于出现重复的数字的情况,如:
题目:
输入一个字符串,按字典序打印出该字符串中字符的所有排列。例如输入字符串abc,则打印出由字符a,b,c所能排列出来的所有字符串abc,acb,bac,bca,cab和cba。
输入:
输入一个字符串,长度不超过9(可能有字符重复),字符只包括大小写字母。
注意此处和之前的是不一样的,但是模版还是一样的,只不过换一种思维:
C++代码:
class Solution {
public:
vector<string>ret;
//判断结果是否已经在ret当中
bool IsEist(vector<string>& a,string& val)
{
for(auto e : a)
{
if(e == val)
{
return false;
}
}
return true;
}
void backtrack(string& str,int start)
{
//如果当start走到最后一个字符的位置
if(start == str.size() - 1)
{
//如果这次结果已经在ret当中就不添加进去
if(IsEist(ret,str))
ret.push_back(str);
}
else
{
for(int i = start;i < str.size();i++)
{
//做选择
swap(str[i],str[start]);
backtrack(str,start + 1);
//撤回
swap(str[i],str[start]);
}
}
}
vector<string> Permutation(string str) {
if(str.size()< 1)
{
return ret;
}
//str是字符串,0代表从哪里开始
backtrack(str,0);
//按字典排序
sort(ret.begin(),ret.end());
return ret;
}
};
四、总结一下
子集问题可以利用数学归纳思想,假设已知一个规模较小的问题的结果,思考如何推导出原问题的结果。也可以用回溯算法,要用 start 参数排除已选择的数字。
组合问题利用的是回溯思想,结果可以表示成树结构,我们只要套用回溯算法模板即可,关键点在于要用一个 start 排除已经选择过的数字。
排列问题是回溯思想,也可以表示成树结构套用算法模板,关键点在于使用 contains 方法排除已经选择的数字。
记住这几种树的形状,就足以应对大部分回溯算法问题了,无非就是 start 或者 contains 剪枝,也没啥别的技巧了。
模版模版模版!!!
