A regressão linear pode ser descrita pela seguinte fórmula:
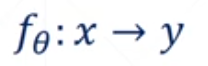
A regressão linear é um problema de predição de valor contínuo, isto é, sob o cálculo de um dado x e parâmetro do modelo θ, a equação correspondente pode ser infinitamente aproximada do valor verdadeiro y.
Aqui está um exemplo simples de previsão de valor contínuo:
y = w * x + b
Quando os dois conjuntos de parâmetros são conhecidos, os parâmetros w e b podem ser obtidos pelo método de eliminação, e a solução exata da equação pode ser obtida. Ou seja, w = 1,477, b = 0,089
1,567 = w * 1 + b
3,043 = w * 2 + b
No entanto, na vida real, muitas vezes é impossível resolvê-lo com precisão. Em primeiro lugar, porque a equação do modelo em si é desconhecida, os dados coletados estão todos com um certo desvio e, em segundo lugar, os dados que observamos muitas vezes são ruidosos. Portanto, um fator de ruído ε precisa ser adicionado à fórmula acima, a saber
y = w * x + b + ε, assumimos ε ~ N (0,1), ou seja, ε obedece a uma distribuição Gaussiana com uma média de 0 e uma variância de 1. A distribuição acima é mostrada na figura a seguir:
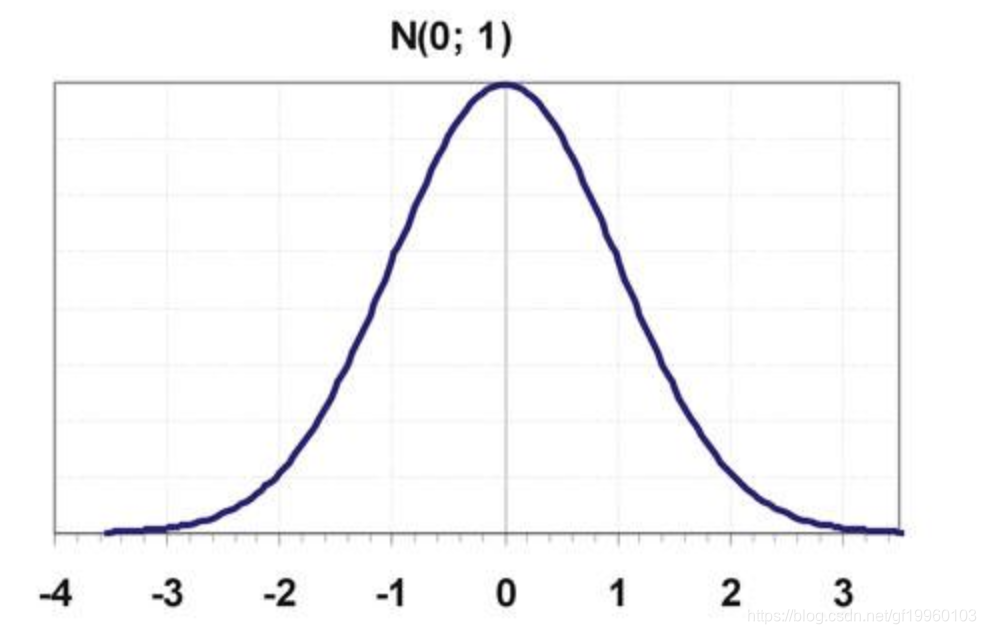
Ou seja, a maioria dos valores são distribuídos perto de 0 e os valores mais distantes de 0 são menos distribuídos.
Por meio da distribuição gaussiana, o processo de solução acima pode ser alterado para:
1,567 = w * 1 + b + eps
3.043 = w * 2 + b + eps
4.519 = w * 3 + b + eps
Quando queremos obter os valores apropriados de w e b, precisamos observar vários conjuntos de dados e, por meio da iteração de vários conjuntos de dados de observação, podemos obter o melhor desempenho geral de w e b.
Então, como resolvemos os dois parâmetros w e b?
Aqui, é necessário introduzir o conceito de função de perda, ou seja, o erro entre o valor verdadeiro e o valor previsto. A fórmula da função de perda é a seguinte:
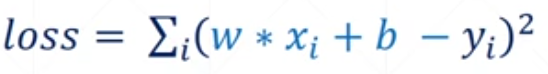
Para obter o melhor desempenho w e b, ou seja, w e b sob a condição de que a função de perda atinja o valor mínimo, a função de perda aqui é a soma dos erros de cada grupo de observações.
Portanto, transformamos o problema de estimar os parâmetros do modelo w e b em um problema de minimizar a função de perda.
Em seguida, usamos o algoritmo de descida gradiente para determinar os parâmetros do modelo w e b. Não vou explicar muito sobre o que é o algoritmo de descida de gradiente aqui. O gradiente pode ser simplesmente entendido como a derivada da função, e a direção do gradiente é a direção em que o valor da função aumenta. Por exemplo:
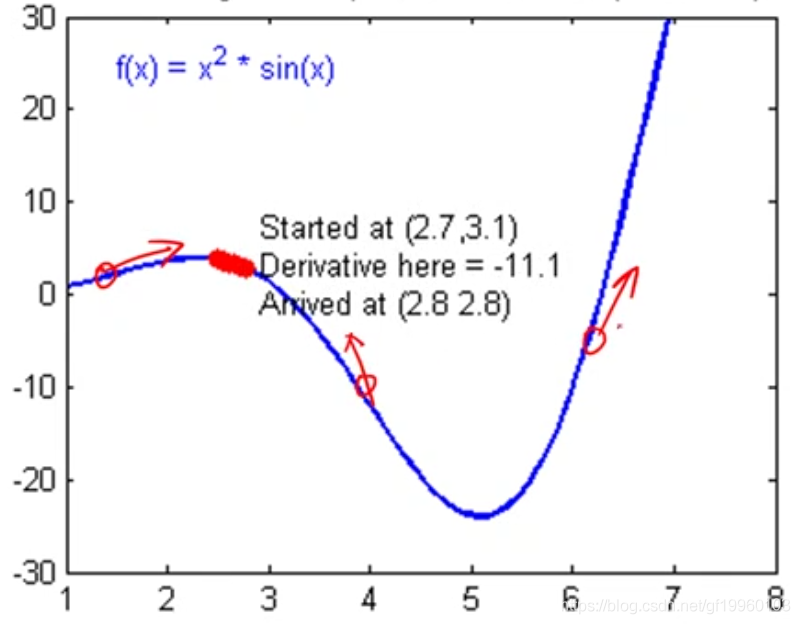
Por exemplo, a função objetivo é f (x), a direção da derivada da função nos três pontos acima aponta para a direção em que o valor da função aumenta. Também pode ser entendida como a direção do valor máximo da função. Quando queremos minimizar a função de perda, resolvemos a função de perda E obtenha web do ponto correspondente, ou seja, os parâmetros do modelo que desejamos obter. Na figura acima, o valor mínimo da função de perda é cerca de 5, deixe os parâmetros do modelo verificarem se o gradiente é alterado na direção oposta. Cada mudança tem um tamanho de passo fixo, ou seja, a taxa de aprendizado. Por meio de iterações repetidas, encontre os parâmetros do modelo ideais .
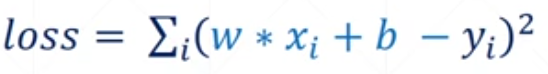
Portanto, precisamos encontrar a derivada parcial da função objetivo, ou seja, calcular w'e b'respectivamente
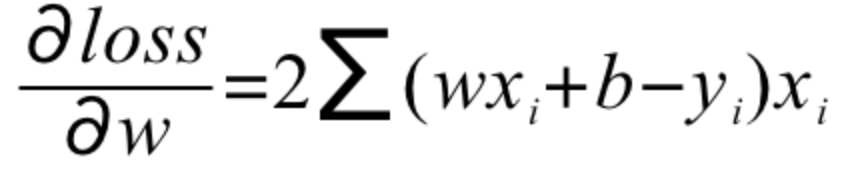
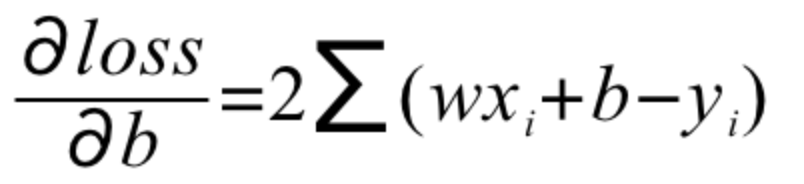
E atualize o gradiente da seguinte maneira
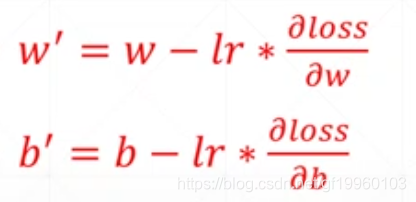
Dedução de código Python:
#!/usr/bin/env python
# -*- coding: utf-8 -*-
__author__ = 'Seven'
import numpy as np
# y = wx + b
def calculate_loss_function(w, b, points):
total_error = 0
for i in range(len(points)):
x = points[i, 0]
y = points[i, 1]
total_error += ((w * x + b) - y) ** 2
return total_error / float(len(points))
def step_gradient(w_current, b_current, points, learning_rate):
w_gradient = 0
b_gradient = 0
N = float(len(points))
for i in range(len(points)):
x = points[i, 0]
y = points[i, 1]
# w_gradient = 2x(wx+b-y)
w_gradient += 2 / N * x * ((w_current * x + b_current) - y)
# b_gradient = 2(wx+b-y)
b_gradient += 2 / N * ((w_current * x + b_current) - y)
new_w = w_current - learning_rate * w_gradient
new_b = b_current - learning_rate * b_gradient
return [new_w, new_b]
def gradient_descent_runner(starting_w, starting_b, learning_rate, num_iterations, points):
w = starting_w
b = starting_b
for i in range(num_iterations):
w, b = step_gradient(w, b, points, learning_rate)
return [w, b]
def run():
# 构建模拟数据并添加噪声，并拟合y = 1.477x + 0.089
x = np.random.uniform(0, 100, 100)
y = 1.477 * x + 0.089 + np.random.normal(0, 1, 1)
points = np.array([[i, j] for i, j in zip(x, y)])
learning_rate = 0.0001
initial_b = 0
initial_w = 0
num_iterations = 1000
print(f'原始损失函数值为:{calculate_loss_function(initial_w, initial_b, points)}, w={initial_w}, b={initial_b}')
w, b = gradient_descent_runner(initial_w, initial_b, learning_rate, num_iterations, points)
print(f'经过{num_iterations}次迭代, 损失函数的值为:{calculate_loss_function(w, b, points)}, w={w}, b={b}')
if __name__ == '__main__':
run()
O efeito da operação é o seguinte:
Como pode ser visto na figura acima, após 1000 iterações, o valor de w é cerca de 1,49, o valor de b é cerca de 0,08, o w real é 1,477 e b é 0,089. O efeito de corrida está muito próximo do valor real.