Aprendizado de máquina Xiaobai observa regressão linear em série

Esta série é voltada para as notas do grupo de estudos DataWhale.Na perspectiva de um iniciante que tem uma base fraca em estatística e teoria de aprendizado de máquina, com base nos materiais de estudo do grupo, o conhecimento é resumido e organizado do superficial ao profundo. O novo entendimento pode continuar a melhorar. Como o nível é realmente limitado, os erros são inevitáveis e os leitores podem criticar e corrigir. Se precisar reimprimir, entre em contato com o blogueiro, obrigado

Conceitos fundamentais de algoritmos de regressão linear

O que é regressão linear?

O modelo de regressão é uma função usada para expressar o relacionamento de mapeamento entre variáveis de entrada (variáveis independentes) e variáveis de saída (variáveis dependentes). Quando a função pertence a uma função linear, é chamada de modelo de regressão linear, que pode ser considerada como uma combinação linear de um ou mais parâmetros do modelo chamados coeficientes de regressão.
Em termos leigos, é uma equação linear usada para expressar quantitativamente a relação quantitativa entre vários indicadores (como o número de quartos, a área do quarto e o preço total da casa).

Formulário de realização geral de regressão linear

Suponha que \ (x_ {1} \) , \ (x_ {2} \) …… \ (x_ {d} \) seja a variável independente do objeto a ser estudado (como número de quartos, área da sala etc.), \ (y \) Para a variável dependente (preço total da casa) relacionada à variável independente, se expressa como uma função linear, o relacionamento entre os dois pode ser escrito como:

\ [\ begin {align *} f (x) & = \ theta_0 + \ theta_1x_1 + \ theta_2x_2 + ... + \ theta_dx_d \\ & = \ sum_ {i = 0} ^ {d} \ theta_ix_i \\ \ end {alinhar*}\]

Onde \ (θ_ {i} \) é o parâmetro do modelo, responsável por ajustar o peso da influência de cada variável independente na variável dependente. O processo de ajuste do modelo de regressão linear pode ser visto como usando o conjunto de dados que obtivemos (amostrado, onde cada conjunto de dados contém o valor de cada variável independente da amostra \ (x_ {i} \) e seu fator correspondente O valor da variável \ (y_ {i} \) ) para encontrar o parâmetro mais adequado \ (θ_ {i} \) , de modo que o valor previsto do modelo \ (f (x) \) seja o mais próximo possível do valor real \ (y \ ) Processo.

Para encontrar os parâmetros mais adequados, deve haver um padrão para avaliar a eficácia do modelo, bem como uma estratégia para ajustar os parâmetros.
O erro quadrático médio, como a soma dos quadrados da diferença entre o valor previsto e o valor real, é um dos indicadores de avaliação mais comumente usados em modelos de regressão linear, a saber:

\ [J (\ theta) = \ frac {1} {2} \ sum_ {j = 1} ^ {n} (f _ {\ theta} (x ^ {(i)}) - y ^ {(i)} ) ^ 2 \]

Nossa tarefa é encontrar os parâmetros ideais do modelo, minimizando o erro quadrático médio.O erro quadrático médio aqui também é chamado de função de custo , que é uma função usada para medir o desvio médio de todos os conjuntos de amostras .

Método de otimização do modelo de regressão linear

A partir da discussão acima, precisamos de uma estratégia de ajuste de parâmetros para minimizar a função de custo.Os métodos mais usados aqui são mínimos quadrados, gradiente descendente, Newton e quase-Newton:

Menos quadrados: Supõe-
se que não haja n amostras (valores observados) no conjunto de dados para um determinado problema, e cada amostra contenha m recursos (variáveis independentes), que podem ser expressos pela matriz como:

\ [X = \ left [\ begin {array} {cccc} (x ^ {(1)}) ^ T \\ (x ^ {(2)}) ^ T \\ \ ldots \\ (x ^ {( n)}) ^ T \ end {array} \ right] = \ begin {bmatrix} x_ {11} e x_ {12} e x_ {13} e \ ldots & x_ {1m} \\ x_ {21} e x_ {22} & x_ {23} & \ ldots & x_ {2m} \\ && \ ldots \\ x_ {n1} & x_ {n2} & x_ {n3} & \ ldots & x_ {nm} \ end {bmatrix} \]

Sua saída (variável dependente) pode ser expressa como:

\ [Y = \ left [\ begin {array} {cccc} y ^ {(1)} \\ y ^ {(2)} \\ \ ldots \\ y ^ {(n)} \ end {array} \ direita]\]

A equação linear pode ser escrita como:

\ [f_ \ theta (x) = X \ theta \]

Através da derivação, o parâmetro ótimo θ pode ser obtido pela seguinte fórmula:

\ [\ theta = (X ^ TX) ^ {(- 1)} X ^ TY \]

O método acima é um método de solução de matriz de mínimos quadrados, que é mais conciso do que outras soluções e também é conveniente para a operação do computador.É um dos métodos mais usados para obter mínimos quadrados.

Descida de gradiente:
a idéia central da descida de gradiente é usar a iteração para atualizar continuamente os parâmetros para fazer com que a função objetivo converja para o valor mínimo.O método de implementação específico é encontrar o valor da função mais degradável na posição atual da função diferenciável (função objetivo) A direção rápida (ou seja, a direção reversa do gradiente, o gradiente pode ser considerado como um vetor formado pela função derivada separadamente de cada variável independente) e, em seguida, a variável independente (ou seja, o parâmetro θ) é atualizada a uma certa velocidade ao longo da direção, como segue Como mostrado:

\ [\ theta_j: = \ theta_j- \ alpha \ frac {\ parcial {J (\ theta)}} {\ parcial \ theta} \]

α é a taxa de aprendizado, que determina o tamanho do passo de cada degrau de descida do gradiente.Quanto maior a taxa, mais rápido o valor da função diminui.No entanto, uma taxa de aprendizado excessivamente grande pode causar não convergência. Derivação de J (θ) na fórmula:

\ [\ begin {align *} \ frac {\ parcial {J (\ theta)}} {\ parcial \ theta} & = \ frac {\ parcial} {\ parcial \ theta_j} \ frac {1} {2} \ sum_ {i = 1} ^ {n} (f_ \ theta (x) ^ {(i)} - y ^ {(i)}) ^ 2 \\ & = 2 * \ frac {1} {2} \ sum_ {i = 1} ^ {n} (f_ \ theta (x) ^ {(i)} - y ^ {(i)}) * \ frac {\ parcial} {\ parcial \ theta_j} (f_ \ theta (x ) ^ {(i)} - y ^ {(i)}) \\ & = \ sum_ {i = 1} ^ {n} (f_ \ theta (x) ^ {(i)} - y ^ {(i )}) * \ frac {\ parcial} {\ parcial \ theta_j} (\ sum_ {j = 0} ^ {d} \ theta_jx_j ^ {(i)} - y ^ {(i)})) \\ & = \ sum_ {i = 1} ^ {n} (f_ \ theta (x) ^ {(i)} - y ^ {(i)}) x_j ^ {(i)} \\ \ end {align *} \]

Aqui, o subscrito j indica o j-ésimo parâmetro, e o sobrescrito i indica o i-ésimo ponto de dados. Substitua $$ frac {\ parcial {J (\ theta)}} {\ parcial \ theta} $$ em uma expressão de atualização de parâmetro expressa como um vetor:

\ [\ theta = \ theta + \ alpha \ sum_ {i = 1} ^ {n} (y ^ {(i)} - f_ \ theta (x) ^ {(i)}) x ^ {(i)} \]

Esse método se torna descendente do gradiente em lote, ou seja, calcula todas as amostras ao mesmo tempo em uma iteração. Quando a função objetivo é uma função convexa, pode-se garantir que atinja o valor mínimo, mas quando o tamanho da amostra for grande, trará uma grande quantidade de cálculo. Para resolver esse problema, as pessoas propuseram um método de descida de gradiente estocástico:

\ [\ theta = \ theta + \ alpha (y ^ {(i)} - f_ \ theta (x) ^ {(i)}) x ^ {(i)} \]

O método de descida de gradiente estocástico possui uma pequena quantidade de cálculo e o programa é executado rapidamente, mas possui as desvantagens de menor precisão e possível convergência para o ideal local. Portanto, um método de descida em gradiente de lote pequeno foi proposto posteriormente, ou seja, um número fixo de amostras foi calculado a cada vez para atualizar os parâmetros, que não serão repetidos aqui.

Método de Newton e métodos quase-Newton:
O método de Newton e o método quase-Newton também são métodos comumente usados para lidar com problemas irrestritos de otimização, e sua característica marcante é a convergência rápida. A idéia básica do método de Newton é usar a expansão de Taylor para aproximar uma função mais complexa na posição atual com uma função linear, aproximar o valor mínimo da função original localizando o valor mínimo da função na região e iterar através da iteração Procure o valor mínimo. A expansão de Taylor da função f (x) e ignorando termos de ordem superior mais de duas vezes fornece:

\ [f (x) = f (x_0) + f '(x_0) (x - x_0) + \ frac {1} {2} f' '(x_0) (x - x_0) ^ 2 \]

Expressa em forma vetorial como:

\ [f (x) = f (x_0) + \ bigtriangledown f (x_0) ^ {T} (x - x_0) + \ frac {1} {2} (x - x_0) ^ {T} \ bigtriangledown ^ {2 } f (x_0) (x - x_0) \]

Encontre o gradiente nos dois lados e faça o gradiente igual a 0:

\ [x = x_0 - \ esquerda (\ bigtriangledown ^ {2} f (x_0) \ right) ^ {- 1} \ bigtriangledown f (x_0) \]

Entre eles, \ (\ bigtriangledown ^ {2} f (x_0) \) é chamado de matriz hessiana, representada por H.
Voltando ao nosso problema de otimização de parâmetro, seja \ (l (\ theta) \) a função de perda, e nossa estratégia atualizada é:

\ [\ theta: = \ theta- \ frac {l '(\ theta)} {l' '(\ theta)} = \ theta - H ^ {- 1} \ Delta _ {\ theta} l (\ theta) \ ]

Entre eles, \ (\ Delta _ {\ theta} l (\ theta) \) é a derivada parcial de \ (l (\ theta) \) para \ (\ theta_i \) , que consiste em encontrar o gradiente. \ (H \) é a matriz hessiana de \ (J (\ theta) \) ,

\ [H_ {ij} = \ frac {\ parcial ^ 2l (\ theta)} {\ parcial \ theta_i \ parcial \ theta_j} \]

Para resumir as etapas completas do método de Newton são:

Defina o valor inicial \ (x_0 \) e o requisito de precisão ε.
Calcule o gradiente \ (\ Delta _ {\ theta} l (\ theta) \) e a matriz Hessiana da função aproximada atual .
Considera-se que, se o módulo do gradiente for menor que o requisito de precisão ε, o modelo converge e para de iterar, caso contrário, continua na próxima etapa.
Itere de acordo com a fórmula de atualização de parâmetro para obter o próximo local do ponto \ (x_1 \) e, em seguida, retorne à segunda etapa.

O cálculo da matriz hessiana é mais complicado e a influência é maior quando existem muitos parâmetros. Portanto, as pessoas propuseram um método quase-Newton e construíram uma matriz simétrica definida positiva B que pode aproximar a matriz de Hessian (ou o inverso da matriz de Hessian) sem a derivada parcial de segunda ordem para concluir o cálculo. Seja \ (x_k \) o valor da k-ésima iteração, os requisitos para a matriz recém-construída são os seguintes (ignore a prova ...):

\ [f '(x_ {k + 1}) - f' (x_k) = f '' (x_k) (x_ {k + 1} - x_k) = H (x_ {k + 1} - x_k) \]

A tabela de resumo das fórmulas de iteração do método quasi-Newton comumente usadas, vistas da Internet: No

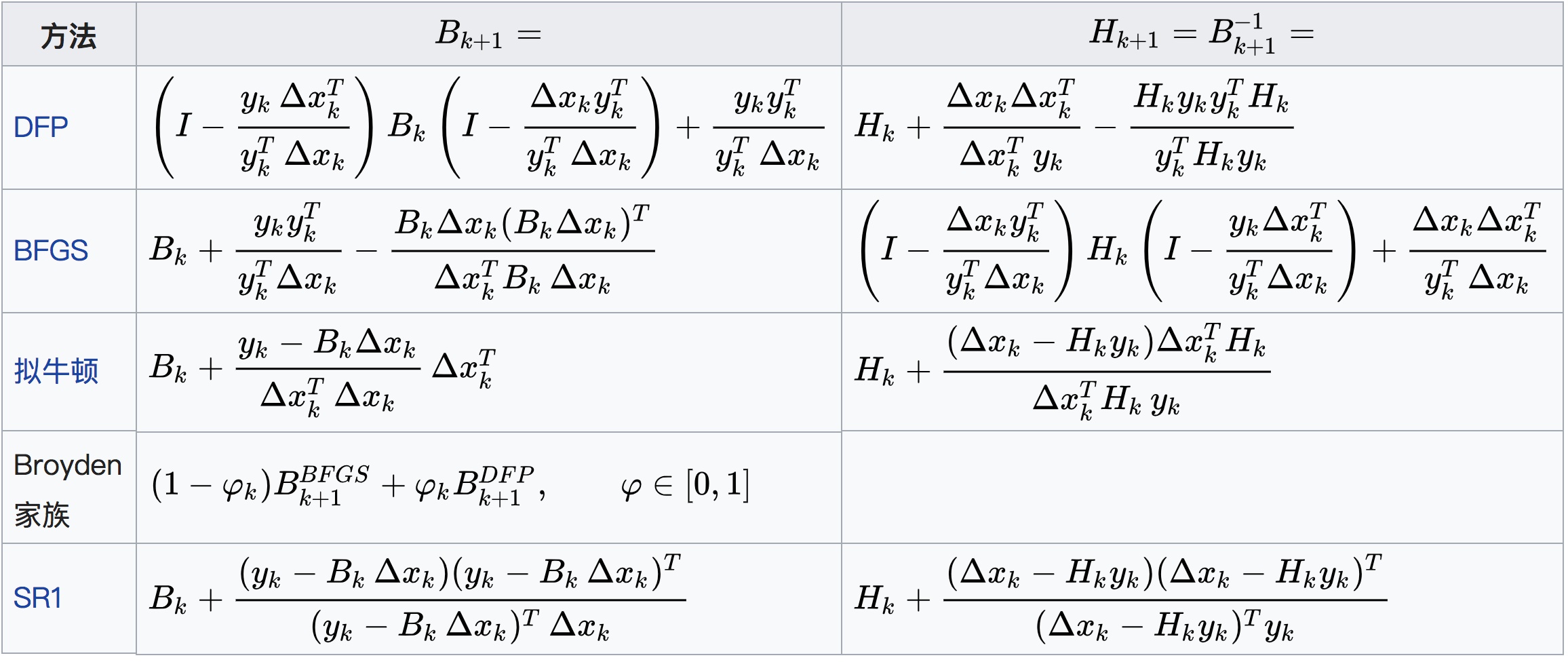
futuro, haverá algumas discussões aprofundadas sobre o método quasi-Newton.

Materiais de referência:

https://github.com/datawhalechina/team-learning/tree/master/ Noções básicas do algoritmo de aprendizado de máquina Materiais de aprendizado do grupo DataWhale
https://baike.baidu.com/item/ regressão linear / 8190345? fr = aladdin Regressão linear da enciclopédia Baidu
https://blog.csdn.net/qq_41800366/article/details/86583789 Explicação do princípio do método de descida de gradiente
https://blog.csdn.net/sigai_csdn/article/details/80678812Como entender o método Newton
https://zhuanlan.zhihu.com/p/46536960 Método de Newton e método quase-Newton