Máquina vectorial de soporte de aprendizaje automático (versión de fórmula de empuje manual)

prefacio

  Máquina de vectores de soporte $(VectordeapoyoV$ $Vecto$ M achine , SVM ) Machine,SVM$)$$Máquina,\_\_\_\_SVM)$ se originó a partir de la teoría del aprendizaje estadístico, es un modelo de clasificación binaria y es el algoritmo más importante en el aprendizaje automático. Sí, es el "más", no uno de$ellos$$.$

1. Márgenes y vectores de soporte

  La idea central del método de clasificación de máquinas de vectores de soporte es encontrar un hiperplano en el espacio de características como el límite de decisión para dividir las muestras en clases positivas y negativas, y hacer que el error de generalización del modelo en el conjunto de datos desconocido sea pequeño. como sea posible.

  Hiperplano: en geometría, un hiperplano es un subespacio de un espacio, que es un espacio cuya dimensión es uno menos que el espacio en el que reside. Si el espacio de datos en sí es tridimensional, su hiperplano es un plano bidimensional, y si el espacio de datos en sí es bidimensional, su hiperplano es una línea unidimensional.

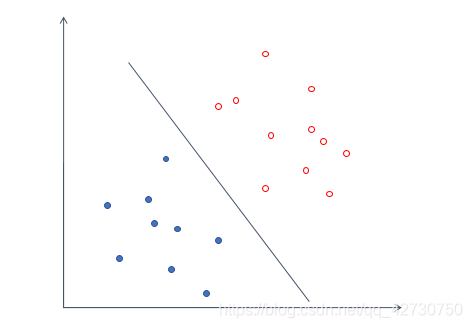
  Por ejemplo, el conjunto de datos anterior, podemos dibujar fácilmente una línea para dividir los datos anteriores en dos categorías, y el error es cero. Para un conjunto de datos, puede haber muchos hiperplanos con un error de 0, como los siguientes:

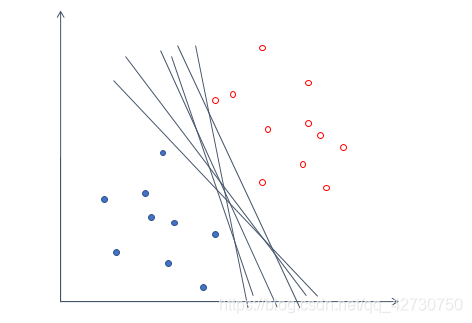
  Pero dicho modelo no puede garantizar un buen rendimiento de generalización, es decir, no puede garantizar que este hiperplano también funcione bien en conjuntos de datos desconocidos. Entonces introducimos un sustantivo ------ 间隔$\left(margen\right)$ es trasladar el hiperplano que encontramos a ambos lados hasta que se detiene en el punto de muestra más cercano al hiperplano para formar dos nuevos hiperplanos. La distancia entre los dos hiperplanos se llama "intervalo",$y$$el$$hiperplano$ está en medio de este "intervalo", es decir, la distancia entre el hiperplano que elegimos y los dos nuevos hiperplanos después de la traducción es igual. Los pocos puntos de muestra más cercanos al hiperplano se denominan支持向量$(vector\; de\; apoyoot)vector$ $vecto)$。$\_$

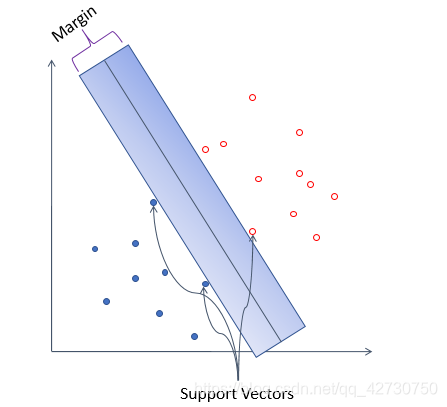
  Comparando las dos figuras anteriores, intuitivamente, las muestras se pueden dividir en dos categorías, pero si se le agrega algo de ruido, es obvio que el hiperplano azul tiene la mejor tolerancia a las perturbaciones locales, porque es "lo suficientemente ancho", si No puedo imaginarlo, mire el siguiente ejemplo:

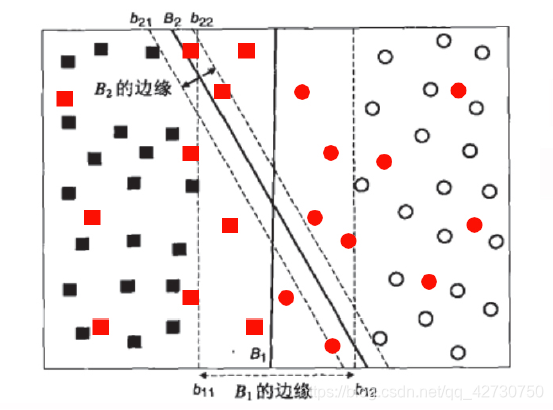
  Obviamente, después de introducir algunas muestras de datos nuevos, $B_{}$Este error de hiperplano sigue siendo 0, y el resultado de la clasificación es el más robusto, $B_{}$Este hiperplano tiene un error de clasificación debido al pequeño intervalo. Por lo tanto, cuando buscamos un hiperplano, esperamos que cuanto mayor sea el intervalo, mejor.
  Lo anterior es la máquina de vectores de soporte, es decir, 通过找出间隔最大的超平面，来对数据进行分类el clasificador de .
  El modelo de máquina de vectores de soporte se puede dividir en los siguientes tres tipos, de simple a complejo:
  $\bullet$ Máquinas de vectores de soporte linealmente separables
  $\bullet$ Máquinas de vectores soporte lineales
  $\bullet$
  MaximizaciónSVM no lineal$($ margen$duro$$margen$$\_$$m\; argen$ $maxximization)$ , aprenda un clasificador lineal, es decir, una máquina de vectores de soporte linealmente separable, también conocida como máquina de vectores de soporte de margen duro; cuando el conjunto de datos de entrenamiento sea aproximadamente separable linealmente, maximice el (soft ($(soft$ $m\; argen$ $maxximization)$ , también aprenda un clasificador lineal, es decir, una máquina de vectores de soporte lineal, también conocida como máquina de vectores de soporte de margen suave; cuando el conjunto de datos de entrenamiento es linealmente inseparable, mediante el uso de la técnica kernel (kernel ($(kernel$ $trckk)y$ maximización de margen suave, aprendiendo máquinas de vectores de soporte no lineales.

  La simplicidad es la base de la complejidad, y también es un caso especial de complejidad.

2. Descripción de la ecuación de la función

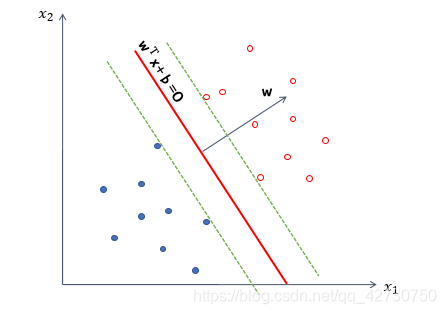
re = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , ... , ( xn , yn ) } , yi ∈ { − 1 , + 1 } re=\{(x_1,y_1   )$D=\{(x_{},y_{}),(X_{},y_{}),\dots ,(X_{},y_{})\},y_{}\in \{-1,+1\}$ , en el espacio de muestra anterior, cualquier línea se puede expresar como:$$w^{TX}\_+b=0$$  其中$w=(w_{},w_{},\dots ,w_{}{)}^T$ es el vector normal, que determina la dirección del hiperplano;$b$ es el término de desplazamiento, que determina la distancia entre el hiperplano y el origen. Obviamente, el hiperplano también puede ser un vector normal$w$ y desplazamiento$BOK$ .
  Para facilitar la derivación y el cálculo, hacemos las siguientes reglas:
  los puntos por encima del hiperplano se marcan como positivos y los puntos por debajo del hiperplano se marcan como negativos, es decir, para$(X_{},y_{})\in D$，若$y_{}=+1$，则有$w^{TX}{\_}_{}+b>0$；若$y_{}=-1$，则有$w^{TX}{\_}_{}+b<0$，表达式如下： { w T xi + segundo ≥ + 1 , yi = + 1 w T xi + segundo ≤ − 1 , yi = − 1 \begin{casos} \bm w^T\bm x_i+b\geq +1, & y_i=+1\\ \\ \bm w^T\bm x_i+b\leq-1, & y_i=-1 \end{casos}⎩ ⎨ ⎧wTX _yo+b≥+ 1 ,wTX _yo+b≤− 1 ,yyo=+ 1yyo=− 1  Entre ellos, +1和-1表示两条平行于超平面的虚线到超平面的相对距离.
  Entonces, cualquier punto $La\; distancia\; de\; x$ al hiperplano se puede escribir como:$$r=\frac{|w^T+b|}{||con||}$$  A partir de esto, la suma de las distancias desde los vectores soporte de dos etiquetas diferentes al hiperplano, es decir, el intervalo, se puede expresar como: $$C=\frac{}{||con||}$$  Nuestro objetivo es encontrar el hiperplano con el mayor intervalo, es decir, el parámetro $w$ y$b$ , tal que$\gamma$最大，即$$\begin{gathered} \underset{w,b}{\mathrm{máximo}}\frac{}{||con||} \\ Subjetoy{}_{}(w^{TX}{\_}_{}+segundo)\ge 1,i=1,2,\dots ,n \end{gathered}$$   Obviamente, maximizando el intervalo$\gamma$ solo necesita ser minimizado$||w||$ es suficiente, por lo que las restricciones son las siguientes:$$\begin{gathered} \underset{w,b}{}\frac{}{2}||w|{|}^2 \\ Subjetoy{}_{}(w^{TX}{\_}_{}+segundo)\ge 1,i=1,2,\dots ,norte \end{gathered}$$

  De hecho, es tomar el recíproco, entonces para qué agregar el cuadrado, como dije antes, $L_{}$Paradigma Bueno, sumar un cuadrado es eliminar la operación de raíz cuadrada y simplificar el proceso de cálculo.

3. Solución de parámetros

  Para resolver problemas de optimización con restricciones, se suele utilizar para introducir el multiplicador de Lagrange $\lambda$ construye la función lagrangiana. De hecho, esto pertenece al problema del extremo condicional de las funciones multivariadas.Puede consultar el extremo condicional de las funciones multivariadas y el método del multiplicador de Lagrange (estándar\Lagrange\multiplicador\método)en el segundo volumen de matemáticas avanzadas.$(métodomul\; i\; a\; li\; ar$ d e$s$$t$$y$$d$$a$$r$$d$$L$$a$$g$$r$$a$$g$$n$$e$$)$$,$$repasemos$$brevemente$$a$$continuación$$.$

3.1 Multiplicadores lagrangianos

  Para encontrar la función $z=f(x,y)$ en la condición adicional$\phi (x,y)=$Para los posibles puntos extremos debajo de$0$$$L(x,y)=f(x,y)+\lambda \phi (x,y)$$   donde,$\lambda$ es un parámetro, encuentre su par$x$、$y$和λ \lambdaLa primera derivada parcial de$\lambda$ , y hacerla cero, luego las ecuaciones simultáneas: { fx ( x , y ) + λ φ x ( x , y ) = 0 fy ( x , y ) + λ φ y ( x , y ) = 0 φ ( x , y ) = 0 \begin{casos} f_x(x,y)+\lambda \varphi_x(x,y)=0\\ \\ f_y(x,y)+\lambda \varphi_y( x ,y)=0\\ \\ \varphi(x,y)=0\\ \end{casos}⎩ ⎨ ⎧Fx( X ,y )+l fx( X ,y )=0Ftu( X ,y )+l ftu( X ,y )=0φ ( x ,y )=0  Con este sistema de ecuaciones resuelve $x$、$y$和$\lambda$ , el obtenido$(X,y)$ es la función$f(x,y)$ en la condición adicional$\phi (x,y)=$Posibles puntos extremos por debajo de$0\; .$
  Si la función tiene más de dos variables independientes y más de una condición adicional, por ejemplo, la función$$tu=f(x,y,z,t)$$ bajo la condición adicional$$\begin{gathered} \phi (x,y,z,t)=0 \\ \psi (x,y,z,t)=0 \end{gathered}$$ , primero puedes hacer la función lagrangiana$$L(x,y,z,t)=f(x,y,z,t)+\lambda f(x,y,z,t)+\mu f(x,y,z,t)$$   entre ellos,$yo,\mu$ es un parámetro, encuentre su par$x$、$y$ ,$z$ ,$t$、$\lambda$和$Derivada\; parcial\; de\; primer\; orden\; de\; \mu$ y conviértala en cero, luego resuelva las ecuaciones simultáneas para obtener$(X,y,z,t)$。

  Ven, veamos un pequeño problema:
  encuentra la función $tu=X^2+y^2+z^2$ en las restricciones$z=X^2+y^2$和$X+y+z=$Los valores máximos y mínimos menores de$4\; .$

3.2 Función dual lagrangiana

  Problemas de optimización convexa: la función en sí es cuadrática $\left(cuadrática\right),$ las restricciones de la función son lineales bajo sus parámetros, tal función se$llama$$un$$problema$$de$$optimización$$convexo$$.$

  Primero construya la función de Lagrange de la máquina de vectores de soporte, es decir, la función de pérdida: $$L(w,b,un)=\frac{}{2}||w|{|}^2+\sum _{yo=1}{a}_{}(1-y_{}(w^{TX}{\_}_{}+b)\left)\right(un{}_{}\ge 0)$$   entre ellos,$a=({un}_{},a_{},\dots ,a_{}{)}^{t.\_}$ _
  Se puede ver que la función de Lagrange se divide en dos partes: la primera parte es la misma que nuestra función de pérdida original y la segunda parte expresa nuestras restricciones. Esperamos que la función de pérdida construida no solo pueda representar nuestra función de pérdida y restricciones originales, sino que también exprese que queremos minimizar la función de pérdida para resolver$w$ y$La\; intención\; de\; b$ , entonces tenemos que empezar con$\alpha$ es un parámetro, resuelve$L(w,b,\alpha )$ , entonces$w$ y$b$ es un parámetro, resuelve$L(w,b,\alpha )$ valor mínimo. Por lo tanto, nuestro objetivo se puede escribir de la siguiente manera:$$\underset{w,b}{}\underset{a_{}\ge 0}{\mathrm{máximo}}L(w,b,un)(un{}_{}\ge 0)$$