2020-12-09 Análisis de la estructura de la red neuronal convolucional de aprendizaje profundo

1. Descripción general de la estructura

En primer lugar, analizamos el procesamiento de imágenes por redes neuronales tradicionales. Si aún usa imágenes en CIFAR-10, hay un total de 3072 características. Si se ingresa la estructura de red normal, cada unidad neuronal en la primera capa tendrá 3072 pesos. Si es más grande Después de ingresar a la imagen del píxel, hay más parámetros, y la red utilizada para el procesamiento de imágenes generalmente tiene una profundidad de más de 10 capas. En conjunto, la cantidad de parámetros es demasiado grande y demasiados parámetros causarán un ajuste excesivo, y la imagen también tiene su propia Funciones, necesitamos utilizar estas funciones para reformar la red tradicional para acelerar la velocidad y precisión de procesamiento.
Notamos que los píxeles de la imagen están compuestos por 3 canales, y aprovechamos esta característica para colocar sus neuronas en un espacio tridimensional (ancho, alto, profundidad), correspondiente a los 32x32x3 de la imagen (tome CIFAR como ejemplo) como se muestra a continuación. : El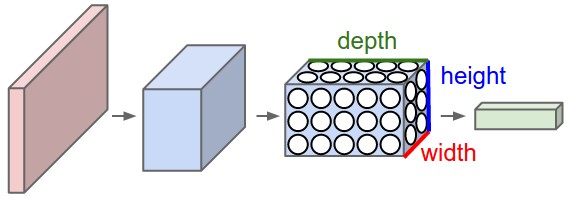

rojo es la capa de entrada donde la profundidad es 3 y la capa de salida es una estructura de 1x1x10. El significado de las otras capas se presentará más adelante, y ahora sabemos primero que cada capa tiene una estructura de altura x anchura x profundidad .

2. Capas de redes neuronales convolucionales

Las redes neuronales convolucionales tienen tres capas: capa convolucional, capa de agrupación y capa completamente conectada (capa convolucional, capa de agrupación y capa totalmente conectada).
Tomemos como ejemplo la red neuronal convolucional CIFAR-10. Una red simple debe contener estas capas:
[INPUT-CONV-RELU-POOL-FC] que es [input-convolution-activación-pooling-class score], Las capas se describen a continuación:

• ENTRADA [32x32x3] Longitud de entrada 32 ancho 32 imagen con tres canales
• CONV: Calcula el área local de la imagen, si queremos usar 12 filtros de fliters, su volumen será [32x32x12].
• RELU: Sigue siendo una capa de excitación máxima (0, x), y el tamaño sigue siendo ([32x32x12]).
• PISCINA: Muestreo a lo largo del (ancho, alto) de la imagen, reduciendo las dimensiones de largo y ancho, por ejemplo, el resultado es [16x16x12].
• FC (es decir, completamente conectado) calcula que el tamaño final de la puntuación de clasificación es [1x1x10], esta capa está completamente conectada y cada unidad está conectada a cada unidad de la capa anterior.

Nota:
1. Los volúmenes y las redes neuronales contienen diferentes capas (por ejemplo, CONV / FC / RELU / POOL también son las más populares)
2. Cada capa ingresa y emite datos de estructura 3D, excepto la última capa
3. Algunas capas pueden no Parámetros, algunas capas pueden tener parámetros (por ejemplo, CONV / FC sí, RELU / POOL no)
4. Algunas capas pueden tener hiperparámetros y algunas capas pueden no tener hiperparámetros (por ejemplo, CONV / FC / POOL sí, RELU no)
La siguiente figura es un ejemplo. No se puede representar en tres dimensiones y solo se puede expandir en una columna.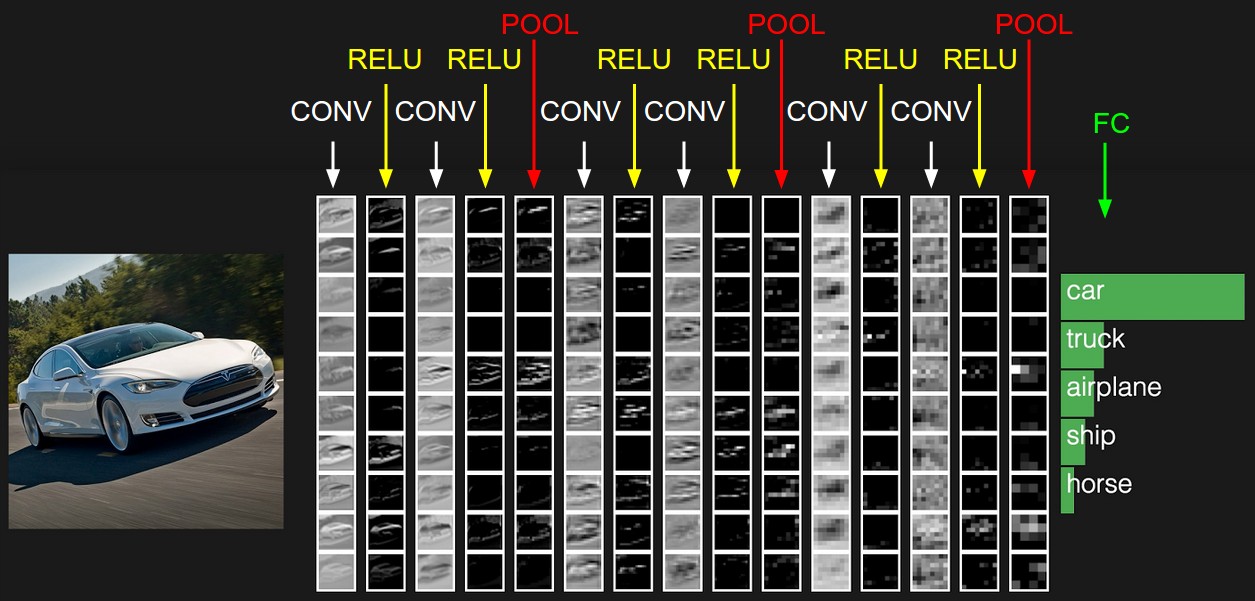

Los detalles específicos de cada capa se analizan a continuación:

2.1 Capa convolucional

La capa convolucional es la capa central de la red neuronal convolucional, lo que mejora enormemente la eficiencia computacional.
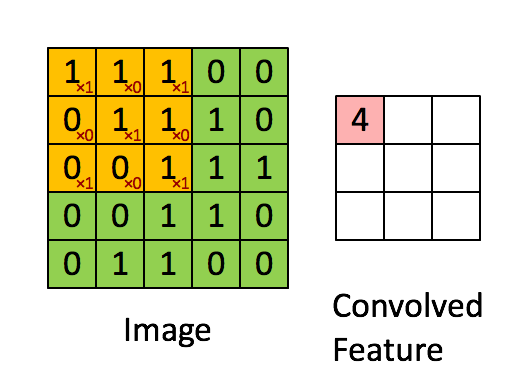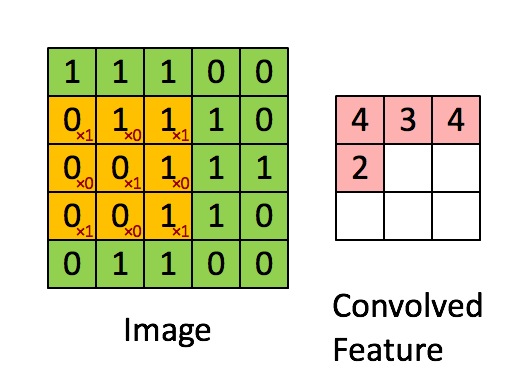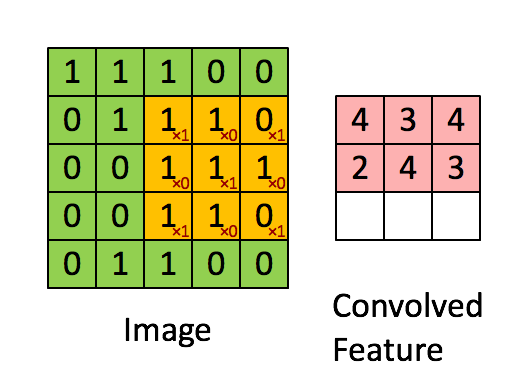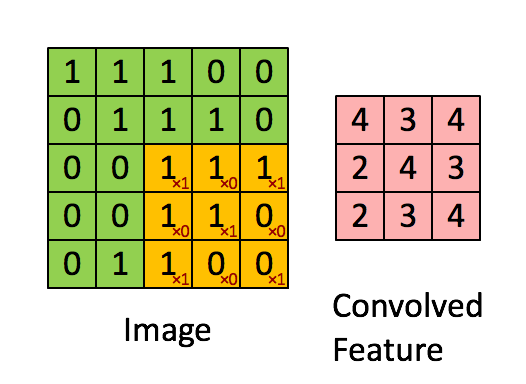
La capa convolucional se compone de muchos filtros, cada filtro tiene solo una pequeña parte, cada vez que solo se conecta a una pequeña parte de la imagen original, la imagen en UFLDL:

este es el resultado de un filtro que sigue deslizándose,
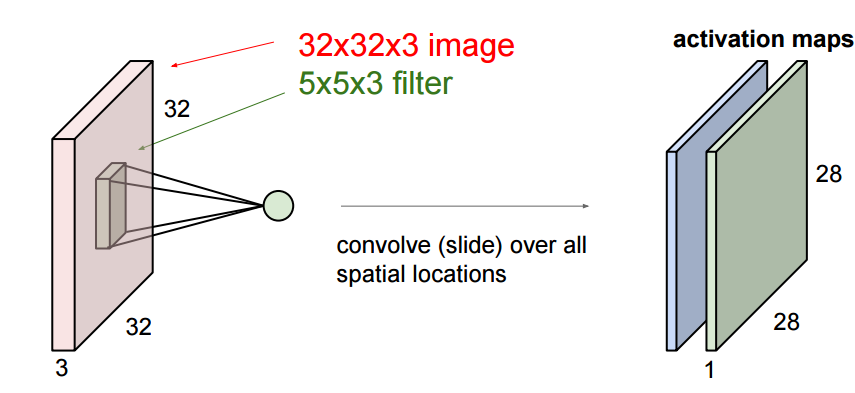
aquí estamos Para profundizar, la imagen que ingresamos es tridimensional, por lo que cada filtro también tiene tres dimensiones. Suponiendo que nuestro filtro es de 5x5x3, también obtendremos un mapeo similar al valor de activación en la imagen de arriba, es decir, convolucionado La característica se llama mapa de activación en la figura siguiente, y su método de cálculo es wT × x + bwT × x + b, donde w es 5x5x3 = 75 datos, que es el peso, que se puede ajustar.
Podemos tener múltiples filtros:

Profundizar , hay tres hiperparámetros cuando deslizamos: 1. Profundidad, profundidad, que está determinada por el número de filtros.
2. Zancada, zancada, el intervalo de cada deslizamiento, la animación anterior solo se desliza 1 número a la vez, es decir, la longitud del paso es 1.
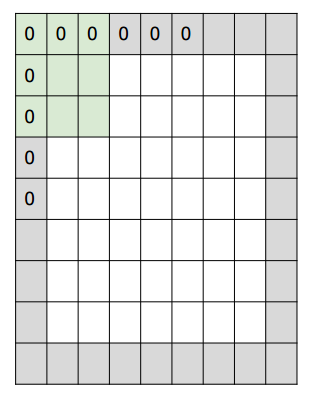
3. El número de relleno de ceros, relleno de ceros, a veces según sea necesario, usará cero Expanda el área de la imagen. Si el número de ceros es 1, la longitud se convierte en +2. La parte gris en la figura

siguiente es el cero del complemento. A continuación se muestra un ejemplo unidimensional:

la fórmula de cálculo de la dimensión del espacio de salida es

(W − F + 2P) / S + 1 (W − F + 2P) / S + 1

Donde w es el tamaño de la entrada, f es el tamaño del filtro, p es el tamaño del relleno con ceros y s es el tamaño del paso. En la figura, si el relleno con ceros es 1, la salida son 5 números, el tamaño del paso es 2 y la salida son 3 números. Hasta
ahora, parece que no hemos involucrado  el concepto de nervio wow, ahora lo entendemos desde una perspectiva neurológica:
cada valor de activación mencionado anteriormente es: wT × x + bwT × x + b, esta fórmula nos es familiar wow, esto Es la fórmula de puntuación de las neuronas, por lo que podemos considerar cada mapa de activación como una obra maestra de un filtro. Si hay 5 filtros, habrá 5 filtros diferentes conectados a una parte al mismo tiempo.
Las redes neuronales convolucionales tienen otra característica importante: el peso compartido : los  pesos de diferentes unidades neuronales (ventanas deslizantes) en el mismo filtro son los mismos. Esto reduce en gran medida el número de pesos.
De esta manera, el peso de cada capa es el mismo, y el resultado de cada cálculo de filtro es una convolución (se agregará un sesgo b más adelante):

esta es también la fuente del nombre de la red neuronal convolucional.
La imagen a continuación es incorrecta, consulte el sitio web oficial  http://cs231n.github.io/convolutional-networks/#conv , descubra el error y comprenda el principio de funcionamiento de la convolución.

Aunque el peso w de cada filtro se cambia aquí en tres partes, la forma de wx + b todavía se usa en la neurona.
-Propagación inversa: la propagación inversa de este tipo de convolución sigue siendo convolución, y el proceso de cálculo es relativamente simple
. Convolución -1x1: algunos artículos utilizan convolución 1 * 1, como la primera  red en red.Esto puede hacer de manera efectiva varios productos internos. La entrada tiene tres capas, por lo que cada capa debe tener al menos tres ws, es decir, el filtro del gráfico dinámico anterior se cambia a 1x1x3.
-Convoluciones dilatadas. Recientemente se han realizado investigaciones (  por ejemplo, ver el artículo de Fisher Yu y Vladlen Koltun ) agregaron un hiperparámetro a la capa convolucional: dilatación. Este es un control adicional del filtro. Activemos el efecto: cuando la dilatación es igual a 0, calcule la convolución w [0] x [0] + w [1] x [1] + w [2] x [2]; dilatación Cuando = 1, se vuelve así: w [0] x [0] + w [1] x [2] + w [2] x [4]; es decir, cada imagen que queremos procesar está separada por 1. Este Esto permite el uso de menos capas para fusionar la información espacial. Por ejemplo, usamos dos capas CONV 3x3 en la capa superior. Esta es la segunda capa que desempeña el papel de 5x5 (campo receptivo efectivo). Si usa convoluciones dilatadas, entonces esto es efectivo El campo receptivo crecerá exponencialmente.

 

2.2 Capa de agrupación

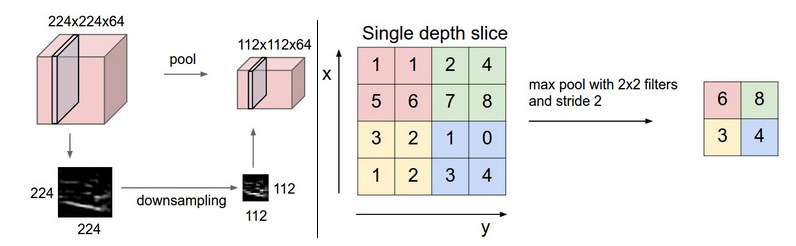
De lo anterior se puede ver que aún existen muchos resultados obtenidos después de la capa convolucional, y debido a la existencia de la ventana deslizante, también se superpone mucha información, por lo que existe una capa de pooling, que divide los resultados obtenidos por la capa convolucional en varios puntos sin superposición. Part, y luego seleccione el valor máximo de cada parte, o el valor promedio, o la norma 2, u otros valores que desee. Tomemos el grupo máximo con el valor máximo como ejemplo:

-Propagación inversa: el gradiente del valor máximo se invirtió antes Ya lo aprendí al propagar, aquí generalmente hacemos un seguimiento del valor máximo de activación, por lo que la eficiencia se mejorará durante la propagación hacia
atrás . -Deshacerse de la agrupación. Algunas personas piensan que la agrupación es innecesaria, como The All Convolutional Net  Mucha gente piensa que ninguna capa de agrupación es importante para los modelos generativos. Parece que la capa de agrupación puede disminuir o desaparecer gradualmente en el desarrollo futuro.

2.3 Otras capas

1. Capa de normalización, en el pasado, la capa de normalización se usaba para simular el efecto inhibidor del cerebro humano, pero gradualmente creo que no es muy útil, por lo que la uso menos. Este artículo presenta su función en la biblioteca cuda-convnet API de Alex Krizhevsky.
2. Capa completamente conectada, esta capa completamente conectada es la misma que hemos aprendido antes Como se mencionó anteriormente, la capa de clasificación final es una capa completamente conectada.

2.4 Conversión de capas FC a capas CONV

Excepto por los diferentes métodos de conexión, la capa completamente conectada y la capa convolucional se calculan en productos internos, que se pueden convertir entre sí:
1. Si el FC hace el trabajo de la capa CONV, es equivalente a que la mayoría de las posiciones de su matriz son 0 (matriz dispersa).
2. Si la capa FC se convierte en una capa CONV. Es equivalente a la conexión parcial de cada capa se convierte en todos los enlaces. Por ejemplo, la entrada de la capa FC con K = 4096 es 7 × 7 × 512, entonces la capa convolucional correspondiente es F = 7, P = 0, S = 1, K = 4096 la salida es 1 × 1 × 4096.
Ejemplo:
supongamos que un cnn ingresa una imagen de 224x224x3 y, después de varios cambios, una capa genera 7x7x512. Después de esto, se utilizan dos capas de 4096 FC y las últimas 1000 FC para calcular la puntuación de clasificación. A continuación se muestra el proceso de conversión de estas tres capas de fc a Conv:
1 .Use la capa conv con F = 7 para generar [1x1x4096];
2. Use el filtro con F = 1 para generar [1x1x4096];
3. Use la capa conv con F = 1 para generar [1x1x1000].

Cada conversión convertirá los parámetros FC en el formato de parámetro conv. Si se pasa una imagen más grande en el sistema convertido, el cálculo avanzará muy rápido. Por ejemplo, si ingresa una imagen de 384x384 en el sistema anterior, obtendrá la salida de [12x12x512] antes de las últimas tres capas, y la capa de conversión convertida arriba obtendrá [6x6x1000], ((12-7) / 1 + 1 = 6). Nosotros Se obtuvo un resultado de clasificación 6x6 con un solo clic.
Esto es más rápido que las 36 iteraciones originales. Esta es una técnica de aplicación práctica.
Además, podemos usar dos capas convolucionales con un tamaño de paso de 16 en lugar de una capa convolucional con un tamaño de paso de 32 para ingresar la imagen de arriba para mejorar la eficiencia.

3 Construye una red neuronal convolucional

A continuación, usaremos CONV, POOL, FC, RELU para construir una red neuronal convolucional:

3.1 Jerarquía

Construimos según la siguiente estructura

INPUT -> [[CONV -> RELU]*N -> POOL?]*M -> [FC -> RELU]*K -> FC

•  

Donde N> = 0 (generalmente N <= 3), M> = 0, K> = 0 (generalmente K <3)
Nota aquí: preferimos usar CONV multicapa y de tamaño pequeño.
¿por qué?
Por ejemplo, 3 3x3 y una capa de convivencia 7x7, todos pueden obtener campos receptivos de 7x7. Pero 3x3 tiene las siguientes ventajas:
1. La combinación no lineal de
3 capas tiene una capacidad expresiva más fuerte que la combinación lineal de 1 capa ; 2. 3 capas El número de parámetros de la capa convolucional de tamaño pequeño es menor, 3x3x3 <7x7;
3. En retropropagación, necesitamos usar más memoria para almacenar los resultados de la capa intermedia.

Vale la pena señalar que las arquitecturas Inception de Google y las Redes residuales de Microsoft Research Asia. Ambas han creado una estructura de conexión más compleja que la estructura anterior.

3.2 Tamaño de la capa

1. Capa de entrada: la capa de entrada está generalmente en forma exponencial de 2, como 32 (por ejemplo, CIFAR-10), 64, 96 (por ejemplo, STL-10) o 224 (por ejemplo, ImageNet ConvNets comunes), 384, 512, etc.
2. Capa convolucional: generalmente un filtro pequeño como 3x3 o máximo 5x5, el tamaño del paso se establece en 1, al agregar relleno de cero, la capa convolucional puede no cambiar el tamaño de la entrada, si debe usar un filtro grande, a menudo está en el primero La primera capa usa el método de relleno de ceros P = (F − 1) / 2.
3. Capa de agrupación: una configuración común es utilizar una capa de agrupación máxima de 2x2, y rara vez hay una capa de agrupación máxima superior a 3x3.
4. Si nuestro tamaño de paso es mayor que 1 o no hay relleno de cero, debemos prestar mucha atención a si nuestro tamaño de paso y filtro son lo suficientemente robustos, y si nuestra red está conectada de manera uniforme y simétrica.
5. Un tamaño de paso de 1 funciona mejor y es más compatible con la agrupación.
6. El beneficio del relleno de cero: si no rellena el cero, la información del borde se descartará rápidamente
7. Considere las limitaciones de memoria de la computadora. Por ejemplo, ingrese una imagen de 224x224x3, el filtro es 3x3, un total de 64 filtros y el relleno es 1. Cada imagen requiere 72 MB de memoria, pero si se ejecuta en la GPU, es posible que la memoria no sea suficiente, por lo que puede ajustar los parámetros como filter a 7x7 y stride a 2 (ZF net ). O filer11x11, zancada de 4. (AlexNet)

3.3 Caso

1. LeNet. La primera aplicación exitosa de cnn (Yann LeCun en la década de 1990). Sus puntos fuertes son los códigos postales, dígitos, etc.
2. AlexNet. El primero ampliamente utilizado en visión por computadora, (por Alex Krizhevsky, Ilya Sutskever y Geoff Hinton). El desafío ImageNet ILSVRC en 2012 brilla, similar a la estructura LeNet pero más profundo y más grande, con múltiples capas convolucionales superpuestas.
3. ZF Net. El ganador de ILSVRC 2013 (Matthew Zeiler y Rob Fergus). Se conoció como ZFNet (abreviatura de Zeiler & Fergus Net). Ajustó los parámetros estructurales de Alexnet, expandió la capa convolucional media para hacer la primera capa de filtros Y el tamaño del paso se reduce.
4. GoogLeNet. El ganador de ILSVRC 2014 (Szegedy et al. De Google.) Redujo en gran medida el número de parámetros (de 60M a 4M). Usando la agrupación promedio en lugar de la primera capa FC de ConvNet, eliminando muchos parámetros, hay muchos Variantes como: Inception-v4.
5. VGGNet. El subcampeón en ILSVRC 2014 (Karen Simonyan y Andrew Zisserman) demostró los beneficios de la profundidad. Se puede usar en Caffe. Pero hay demasiados parámetros, (140M), y muchos cálculos. Pero ahora hay muchos Los parámetros se pueden eliminar.
6. ResNet. (Kaiming He et al). Ganador de ILSVRC 2015. A 10 de mayo de 2016, este es el modelo más avanzado. También hay una versión mejorada de  Identity Mappings in Deep Residual Networks (publicado en marzo de 2016) .
   Entre ellos, VGG El costo de cálculo es:

INPUT: [224x224x3]        memory:  224*224*3=150K   weights: 0
CONV3-64: [224x224x64]  memory:  224*224*64=3.2M   weights: (3*3*3)*64 = 1,728
CONV3-64: [224x224x64]  memory:  224*224*64=3.2M   weights: (3*3*64)*64 = 36,864
POOL2: [112x112x64]  memory:  112*112*64=800K   weights: 0
CONV3-128: [112x112x128]  memory:  112*112*128=1.6M   weights: (3*3*64)*128 = 73,728
CONV3-128: [112x112x128]  memory:  112*112*128=1.6M   weights: (3*3*128)*128 = 147,456
POOL2: [56x56x128]  memory:  56*56*128=400K   weights: 0
CONV3-256: [56x56x256]  memory:  56*56*256=800K   weights: (3*3*128)*256 = 294,912
CONV3-256: [56x56x256]  memory:  56*56*256=800K   weights: (3*3*256)*256 = 589,824
CONV3-256: [56x56x256]  memory:  56*56*256=800K   weights: (3*3*256)*256 = 589,824
POOL2: [28x28x256]  memory:  28*28*256=200K   weights: 0
CONV3-512: [28x28x512]  memory:  28*28*512=400K   weights: (3*3*256)*512 = 1,179,648
CONV3-512: [28x28x512]  memory:  28*28*512=400K   weights: (3*3*512)*512 = 2,359,296
CONV3-512: [28x28x512]  memory:  28*28*512=400K   weights: (3*3*512)*512 = 2,359,296
POOL2: [14x14x512]  memory:  14*14*512=100K   weights: 0
CONV3-512: [14x14x512]  memory:  14*14*512=100K   weights: (3*3*512)*512 = 2,359,296
CONV3-512: [14x14x512]  memory:  14*14*512=100K   weights: (3*3*512)*512 = 2,359,296
CONV3-512: [14x14x512]  memory:  14*14*512=100K   weights: (3*3*512)*512 = 2,359,296
POOL2: [7x7x512]  memory:  7*7*512=25K  weights: 0
FC: [1x1x4096]  memory:  4096  weights: 7*7*512*4096 = 102,760,448
FC: [1x1x4096]  memory:  4096  weights: 4096*4096 = 16,777,216
FC: [1x1x1000]  memory:  1000 weights: 4096*1000 = 4,096,000



TOTAL memory: 24M * 4 bytes ~= 93MB / image (only forward! ~*2 for bwd)
TOTAL params: 138M parameters

•  

Tenga en cuenta que cuando la memoria se usa más, en las primeras capas CONV, los parámetros están básicamente en las últimas capas FC ¡La primera FC tiene 100M!

3.4 Uso de memoria

La memoria se consume principalmente en los siguientes aspectos:
1. Una gran cantidad de valores de activación y valores de gradiente. Al realizar la prueba, solo puede almacenar el valor de activación actual y descartar los valores de activación anteriores en las capas inferiores, lo que reducirá en gran medida la cantidad de almacenamiento del valor de activación.
2. El almacenamiento de los parámetros, el gradiente durante la propagación hacia atrás y la caché cuando se utilizan momentum, Adagrad o RMSProp ocuparán espacio de almacenamiento, por lo que la memoria utilizada por los parámetros estimados generalmente debe multiplicarse por al menos 3 veces
. 3. Cada vez que se ejecuta la red Recuerda todo tipo de información, como el lote de datos gráficos, etc.
Si se estima que la memoria requerida por la red es demasiado grande, puedes reducir adecuadamente el lote de imágenes, después de todo, el valor de activación ocupa mucho espacio de memoria.

otra información

1. Puntos de referencia de Soumith para el rendimiento de CONV
2. Demostración en  tiempo real de ConvNets del navegador de demostración ConvNetJS CIFAR-10 .
3. Caffe , la popular herramienta de ConvNets
4. ResNets de última generación en Torch7