Exam fairness is an important aspect in evaluating exam quality and is also an issue that has received widespread attention. Although modern education tends to be modernized and many teachings can be realized through computers, there are also many problems that cannot be solved by computers. This is because most exams cannot be separated from the personal review of judges, because computers cannot solve many academic problems. You know, so the workload can only be artificially evaluated. The most important thing is the reasonable and even distribution of test papers.
In the grading work of the college student mathematical modeling competition, M judges (M judges are from different schools) have to complete the scoring of N test papers. The competition test papers come from K schools. The i-th school has Ni copies of the competition test papers, which is To save manpower, each test paper only needs to be scored by p (p<M <K << N) judges.
1. According to the principle of avoidance, the judges are required not to read the test papers of their own schools. It is required to provide a mathematical model for a reasonable and even distribution plan of test papers so that the grading workload of each judge is balanced and the distribution of test papers is balanced and dispersed.
2. Due to special reasons, judges from P schools cannot participate in the evaluation. There are two options: (1) MP judges will participate in the evaluation; (2) P judges will be selected from schools that can participate in the evaluation. Let’s try to discuss the modifications of Model 1 through different choices.
Question one:
Question 1 is obviously a linear programming problem. In order to solve this problem, a combinatorial optimization method can be used to design a test paper distribution plan to achieve a balanced grading workload of judges and a balanced and decentralized distribution of test papers.
Suppose there are M judges and N test papers. The judges are numbered from 1 to M and the test papers are numbered from 1 to N. We introduce the following variables and parameters:
Variables:
- xij: xij is 1 if judge i is assigned to grade paper j, 0 otherwise. Among them, the value range of i is 1 to M, and the value range of j is 1 to N.
Parameters:
- K: the total number of schools
- Ni: the number of test papers in school i
- p: the number of judges who need to score each test paper
Objective function:
The goal is to make the judges' grading workload as balanced as possible, which can be measured by the variance of the judges' total workload. Define the total workload W as the sum of the workload of all judges, then the objective function can be expressed as minimization:
minimize Σ(i=1 to M) [(Σ(j=1 to N) xij) - (W/M)]^2
Constraints:
1. Each test paper can only be scored by p judges:
Σ(i=1 to M) xij = p, for all j = 1 to N
2. Judges cannot review examination papers from their own schools:
xij = 0, for all i = 1 to M and j = 1 to N where i and j represent the same school
3. All xij must be 0 or 1:
xij ∈ {0, 1}, for all i = 1 to M and j = 1 to N
The corresponding code is as follows: (For complete documentation, see the link at the end of the article)
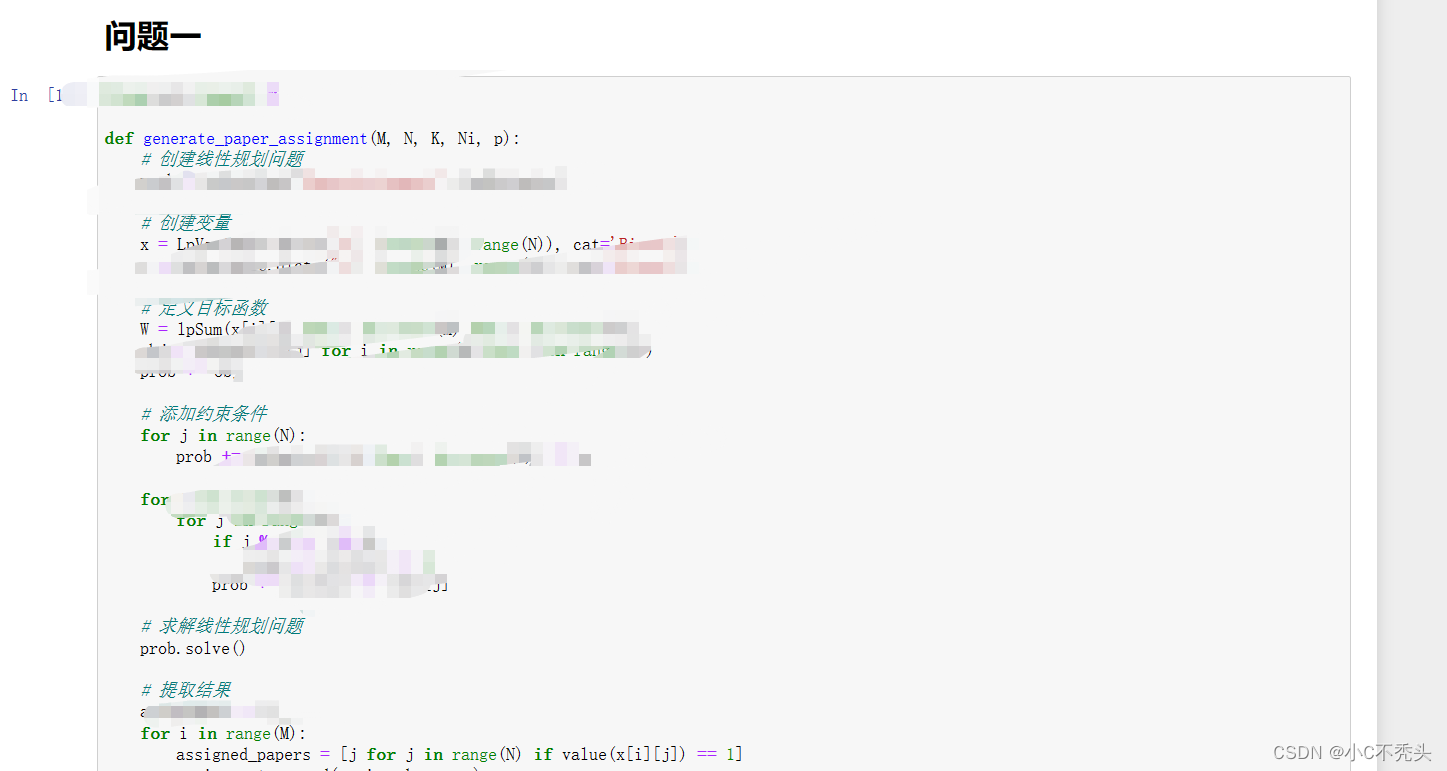
Substitute custom parameters into the program to view the results:

Question two:
Question 2 is actually to add constraints to the model built for the problem. For the specific modeling process, see the link at the end of the article:

Question 2 code implementation: For the specific process, see the link at the end of the article:

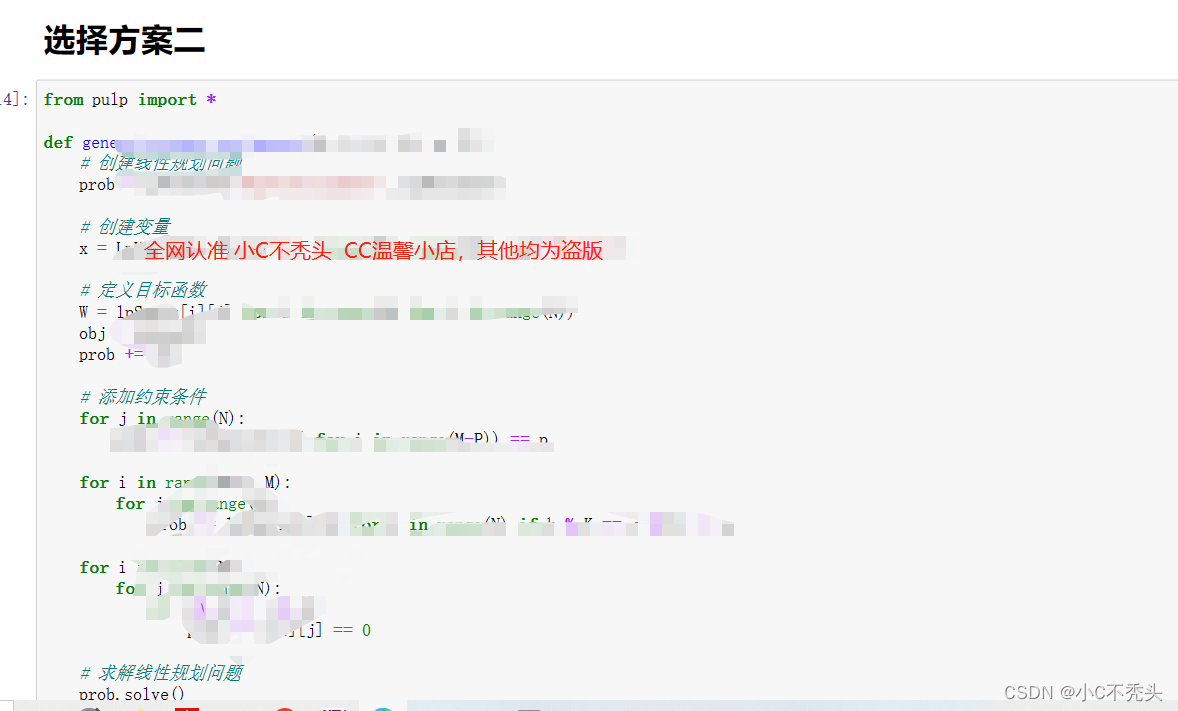
How to obtain specific documents:
