Refinement of "Guide to Discrete Mathematics" - Chapters 6 and 7 (type set theory, predicate logic)

“The more you know, the more you realize how much you don’t know.” - Socrates

introduction

The author has always felt that discrete mathematics is an extremely important knowledge base in the study of computer science. The idea of ​​discretization is reflected in all aspects of computer science. For example, the concept of "pixel" is familiar to us in our daily life. Splitting a picture into tiny pixels is to use the idea of ​​discretization. In order to help everyone lay a solid foundation of thinking in discrete mathematics, the author has opened a new column to refine the book "Guide to Discrete Mathematics" to make it easier to understand. This article is the third part of this column, mainly introducing chapters 6-7.
Chapter 1-3 Portal Portal
Chapter 4-5 Portal

text

Chapter 6 Type Set Theory

type of need

It doesn't make sense to have a collection with different types. We stipulate that the elements in a collection must be of the same type.
Empty sets also have types, and an empty set of natural number type is not the same as an empty set of set type.

collection description

A collection description takes the form:

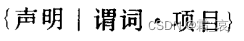
1. Declaration: Declare which type the element belongs to (actually not necessarily the elements in this collection)
2. Predicate: It acts as a filter, and elements that do not meet the requirements of the predicate are not included in the set
3. Item: How the elements in the collection are output.

Let's use an example to illustrate:

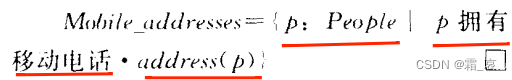
Among them, the first red line declares that p is of type people, the second red line requires that only p that "has a mobile phone" can be retained, and the third red line requires that the collection actually contains each The address() function of each p element, that is, the address of each p.

In practice, both the predicate and the item can be omitted.

abbreviation

Two natural numbers x, y, we can use x...y to represent [x, y].

Cartesian product (emphasis)

1. Order pair: x, y are two elements of any type, then (x, y) is an order pair.
2. Cartesian product: Cartesian product is a collection of ordinal pairs. Let's take an example to understand the Cartesian product:

If A={1, 2}, B={m, n}, then the Cartesian product of A and B, represented by A×B, is {(1, m), (1, n), (2, m), (2,n)}.

3. The type of ordinal pair: if 1 is of N (natural number) type and a is of letter (letter) type, then (1, a) is of N×letter type.
   Note: (1,a) and (a,1) are different types.

The Cartesian product of any set and the empty set is the empty set.

4. Note: We assume that the element type of set A is a, the element type of set B is b, and the element type of set C is C, then the type of A×B×C is ((a,b),c), which is not intuitive of (a, b, c).
5. Component screening: use the . operator for component screening, continue with examples:

{p:A×B|p=(a,b) p.1}, this set is {a}, which is the first part of all elements p. If p has two (a, b), (c, d), then the previous set is {a, c}.

Axiom definition

We can use axiom definitions to define a set:

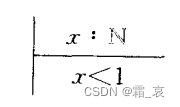
Unlike predicate descriptions, axiom definitions can also declare sets directly:

1. This axiom definition declares the elements of a collection, similar to the predicate description above
   
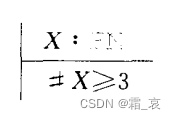
2. The following axiom definition directly declares the set (P(N) is the power set of N, and the statement means that X is a subset of N)
   
   

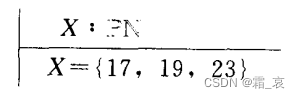
Chapter 7 Predicate Logic

Predicate logic is actually a concise way of writing propositional logic.

Universal quantifier ∀, existential quantifier ∃

There is nothing to say about these two, everyone knows it.

satisfiability, validity, unsatisfiability

A statement formed by predicate logic is a proposition and therefore also has a truth value.

1. Validity: When the variable in a predicate takes any value of the domain and the proposition is true, we call this predicate (note that it is a predicate, not the entire proposition) valid.
   
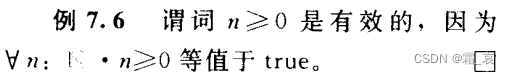
   The universal quantifier means that n takes any value of its domain.
2. Satisfiability: When the variable in the predicate takes a certain value of the domain, the proposition is true, then the predicate is said to be satisfiable.
   
   Existential quantifiers indicate that n takes a certain value in its domain.
3. Unsatisfiability: The proposition that the variable takes any value is false, and the predicate is unsatisfiable, needless to say.

free variable, constrained variable

A variable with a domain is a free variable, otherwise it is a constrained variable. For example:

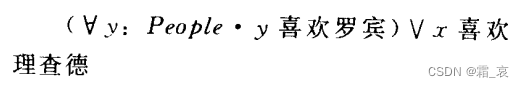
where y has a domain and is a constrained variable, and x is a free variable.
Note: The definition domain has its own scope of influence, and the variable outside the scope of influence is still a free variable.

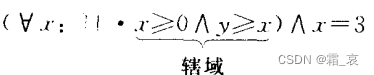
replace

The replacement symbol is [], we use an example to illustrate:

The result of n>0[3/n] is 3>0, that is, write all n places as 3.

Only free variables can be replaced. Constrained variables are restricted by the domain. If they are replaced, there will be one less symbol in the domain, and the meaning is completely different. For example:

The result of ∀n: N·n>0[3/n] is ∀n: N·n>0, which is unchanged. If it is replaced, it will be ∀n: N·3>0, so the symbol n in the domain of definition will disappear, which is obviously not acceptable.

Sequential replacement and simultaneous replacement

When replacing multiple variables, there are two ways of sequential replacement and simultaneous replacement.

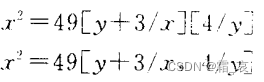
The former is sequential replacement, the latter is simultaneous replacement. There is no difference between the two, except that the former is replaced in two steps, and the latter is replaced directly in one step.

variable capture

If a constrained variable is used to replace a free variable, then this variable is also limited by the domain of definition, and variable capture occurs.
The solution is also very simple, just change the letter to replace the free variable, or change the constraint variable to a letter.

limit

Restrictions are actually predicates in propositional logic. Let me give you an example:

the part of the red line is the limitation of this propositional logic.

Restricted Transformation (Difficulty)

Restricted transformation is the transformation of a restricted statement into an unrestricted statement. For universal quantifiers and existential quantifiers, the conversion methods are different. The details are as follows:

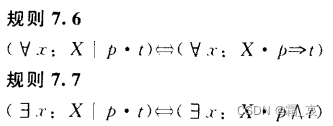
It can be seen that the statement of the universal quantifier uses the implication symbol after conversion, while the statement of the existential quantifier uses the conjunction symbol. In fact, it is not difficult to understand. You can give an example of universal quantifiers and existential quantifiers yourself, and then you will find that universal quantifiers can be described by the sentence pattern "if..., then...", while existential quantifiers are generally described by "...of... "More appropriate.
For example, the following statement:

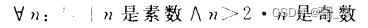
This sentence can be said to be " If n is a natural number, n is a prime number and greater than 2, then n is an odd number."
Look at the following statement:

This sentence obviously reads "There is a female Prime Minister of the United Kingdom "More appropriate.

unique existential quantifier

The only existential quantifier means "there is and only", let us give an example to illustrate:

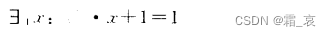
this description means "there is and only one x, so that x+1=1".

There is also a symbol μ for this x:

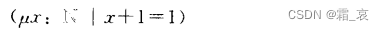
this description represents the set of x that satisfies this condition, and there is only one element in this set.
Note: This notation has no meaning if you count more than one element in the set. This notation is specific to unique existential quantifiers.

Equivalence Reasoning

We have introduced the equivalent reasoning of propositional logic. As an extension of propositional logic operations, predicate logic certainly has its own equivalent reasoning formula. Different from predicate logic, the equivalent reasoning formula here is far away from our inertial thinking, so it needs to be listed, but it is still not necessary to explain each one:

1. The following formula is unexpected, but easy to understand:
   
   
   
   
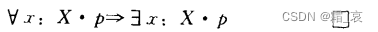
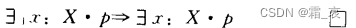
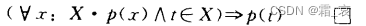
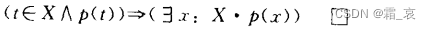
2. The following formula is obvious:
   
3. The following four formulas require careful consideration. Note that the premise of these four formulas is that x does not appear in q:
   
   
   
   
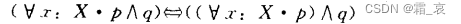
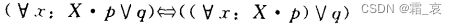
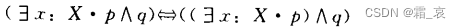
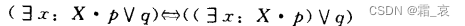
   since x does not appear in q, then x has no relationship with q, so q can naturally be taken out of the brackets.

natural deduction

Predicate logic naturally also has its own natural deductive formula. Before stating these formulas, a reminder that in natural deduction, the upper part is the premise and the lower part is the conclusion. In addition, since the universal quantifier is a generalized intersection operation, and the existential quantifier is a generalized union operation, the description with these two quantifiers can be divided into multiple intersection or union operations to understand: explain this formula, this formula refers to


any The x in the X set can be deduced through several steps to obtain p, then the conclusion is established.

This rule is not easy to understand. The author’s understanding is: if there is x that makes p true, and q can be deduced from the assumption that p is true, then q can also be true; but x does not appear in q, then the truth of q It has nothing to do with x, that is to say, the truth or falsehood of q cannot be changed from the perspective of x. Let me give an example to understand this point. See this description below:

∃x|x∈N·y

Obviously, whether this description is true has nothing to do with the value of x. Then if the existence of x makes this statement true, then it is also true for all x.
Going back to the explanation just now, the true value of q has nothing to do with the value of x, so as long as there is one x, q is true, then for all x, q is true, and the conclusion holds.
This rule also holds for multiple propositions:

one-point rule

The rule is as follows:

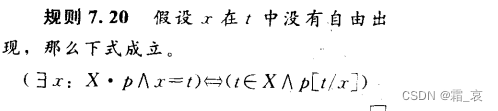
As the rule says, it follows that t is an element of X and that t satisfies p. Note that the premise that x does not appear freely in t is very important. If x is replaced by t containing x, it is obviously impossible to draw what elements can satisfy p.

I am Shuang_Ai, a newcomer working hard on the road of algorithms, thank you for reading! If you think it is good, you can pay attention to it, and I will bring more and more comprehensive algorithm explanations in the future!