Discrete Mathematics-Algebraic System

Binary operation

Basic concepts of binary operations

The concept of computing

Opposite number operations on integer sets

Addition operations on natural number sets

Any one or two elements in the set can be operated on, and the result of the operation is unique.
The concept of operation

Subtraction is not a closed binary operation on the set of natural numbers N
Division is not a binary operation on the set of integers I
Division is a closed binary operation on the set of real numbers R

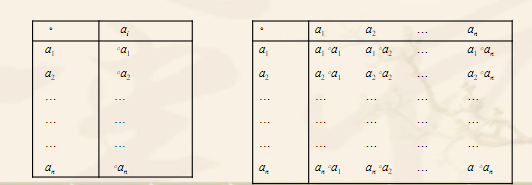
Operation representation and operation table

Operation table: used to represent operations on finite sets

The nature of binary operations

Closure:

Let * be a binary operation on X. If for any x, y∈X, there is x * y∈X, then * is said to be closed on X.
For example, addition and multiplication on the set of natural numbers N are closed, but subtraction is not. From the operation table, it is easy to see whether the operation is closed.
How to observe whether the operation table is closed.
No new elements appear in the operation table

Exchangeability

Let * be a binary operation on X. If for any x, y∈X, there is x * y∈y * x, then * is said to be commutative on X.
Addition, multiplication, intersection, union, and symmetric difference are commutative.

If an operation table is symmetrical on the main diagonal, then this operation is commutative.

Combinability

Let * be a binary operation on X. If for any x, y, z∈X, there is (x * y) * z∈x * (y * z), then * is said to be commutative on X.
The following operations are combinable:
the addition and multiplication of values, the intersection, union, and symmetric difference of sets, the composition of relations, the composition of functions, the conjunction and disjunction of propositions.
If ★ is a combinable operation, the ★ operation of element x can usually be written in the form of exponentiation. as follows:

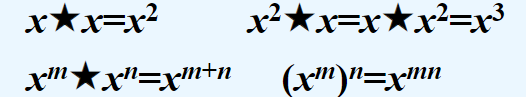
Distribution law

Suppose ★ and * are binary operations on X, if for any x, y, z ∈ X,
x ★ (y * z)=(x★y) * (x★z) (left distributive law)
( x * y)★z=(x★z) * (y★z) (right distributive law)
then it is called ★ to * distributable
distributive law must be two operations, and satisfy both left and right distributive. And also consider who assigns to whom the outside of the parentheses can be assigned to the inside of the parentheses.
For example: Multiplication can be assigned to addition. U and ∩ of the set can be assigned to each other. Disjunctions and conjunctions of propositions are mutually assignable.

Absorption law

Suppose ★ and * are binary operations on X, if for any x, y ∈ X,
x ★ (x * y)=x
x * (x ★ y)=x,
then ★ and * are said to satisfy the absorption law.
For example : U and ∩ of the set satisfy the absorption law. The disjunction and conjunction of propositions satisfy the law of absorption

. There are two ways to prove in mathematics. For example, here we can use definitions to prove that we must first know what is closeable, combinable, and distributable. The second way is to use theorems to prove, and we only learned the definitions here. After understanding these definitions, our proof is relatively simple.


Summary of the nature of operations

Special elements in binary operations

Idempotent

Let ★ be a binary operation on X. If a ∈ X satisfies a★a=a, then a is the idempotent element of ★ operation on X. If there is .x★x=x for any x∈X, it is said that ★ is idempotent on X.
If the element of the idempotent main diagonal of the ∩ operation is the same as

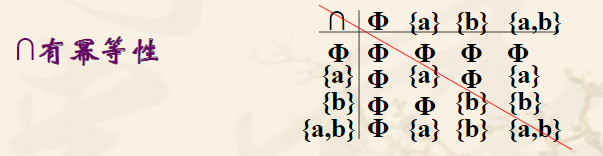
the element of the upper header (or the left header), it is idempotent

Unitary

Let ★ be a binary operation on X, if there is eL ∈ X, so that for any x ∈ X, there is eL★=x, then eL is the left unitary element relative to ★.
If there is eR∈X, so that for any x∈X, x*eR=x, then eR is the right unitary relative to ★.
If eL=eR=e, for any x∈X, there is x★e= e★x=x, then e is the unitary relative to ★.
Unitary yuan can also be called identity yuan, identity yuan.
●Addition + operation on the set of real numbers R, unitary is 0;
because 0+a=a+0=a (a is any real number)
●Multiplication X operation, unitary is 1;

subtraction does not exist unitary, but right Unitary

The theorem


x maps to the y end and is unique. If the x end is fixed, then y must be unique.

Zero dollar

Let ★ be a binary operation on X, if there is θL∈X, so that for any x∈X, there is θL★x=θL, then θL is the left zero element relative to ★.
If there is θR∈X, so that for any x∈X, x★θR=θR, then θR is the right zero element relative to ★.
If θL=θR=θ, for any x∈X, θ★x=x ★θ=θ, said θ is the zero element relative to ★

For example: multiplication X on the set of real numbers, the zero element is 0;
because aX0=0Xa=0 (a is any real number) the
union operation ∪ on the set family, the zero element is
the intersection operation ∩ on the set family of the complete set E , and the zero element is ∅;

Let ★ be a binary operation on X. If there is a left zero element θL∈X and a right zero element θR∈X, then θL=θR=θ, and the zero element θ is unique.
Let ★ be a binary operation on the set X, and |X|>1. If there are unite e and zero element θ in the algebraic system, then θ≠e
proof: use the method of proof by contradiction.
Assuming θ=e, then for any
x∈X, there must be x=ex=θx=θ=e.
This means that all elements in X are the same, so θ≠e

Inverse element

Let ★ be a binary operation with a unitary e on X, x∈X, if xL-1∈X, so that xL-1★x=e, then xL-1 is the left inverse of x relative to ★.
If there is xR-1∈X, so that x★xR-1=e, then xR-1 is the right inverse of x relative to ★.
If xL-1=xR-1=x-1, then x-1★x=x★x-1=e, x-1 is the inverse of x relative to ★. It is also said that x-1 and x are mutually inverse elements. Such as x-1 ∈ X, also called x reversible.

Note: The inverse element must have a unitary element, and the inverse element must involve a certain element.

Example: + and X on the set of real numbers R, x∈R
for addition +: x-1=-x
because e=0, x+(-x)=0
for multiplication X: x-1=1/x (x≠ 0)
Because e=1, x X 1/x=1

inverse element uniqueness theorem,
suppose ★ is a binary operation that has a unitary e on X and can be combined. If x ∈ X, both the left and right inverse elements of x exist , Then the left and right inverse elements of x must be equal, and the inverse element of x is unique.

Other properties of binary operations

Let ★ be a binary operation on X, a ∈ X, if for any x, y ∈ X, there is (a★x=a★y)=>x=y or
(x★a=y★a)=> x=y.
Then it is said that a is a relatively eliminated element of ★.
If for any a ∈ X and a≠θ, a is an erasable element, then it is said that the ★ operation is erasable on X.

For example, for multiplication, for any real number a≠0, a is eliminable.
Because when a≠0, if ax=ay, then x=y.
Therefore, multiplication can be eliminated on the set of real numbers.
However, the ∪ and ∩ operations on the set family do not satisfy the eliminability.
Because AUB= AUC or A∩B= A∩C,
there is not necessarily B=C.
Let ★ be a binary operation that can be combined on X. If a ∈ X, and a-1 ∈ X, then a is an eliminable element.

Summary of Special Elements of Binary Operations

Example: The following are three operation tables
(1) Explain that those operations are commutative, associative, and idempotent.
(2) Find the unitary, zero-element, and inverse element

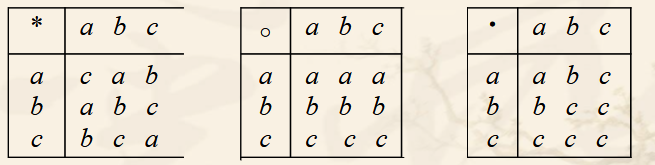
solutions of all reversible elements of each operation : (1)*The operation satisfies the commutative law and the associative law, but does not satisfy the idempotent law.
(2) The o operation does not satisfy the commutative law, the associative law, and the idempotent law.
(3) The operation satisfies the commutative law and the associative law, Does not satisfy the idempotent law.
Explanation: The judgment of the associative law needs to be verified for each choice of operation elements. If |A|=n, it is generally necessary to verify n3 equations.
Identity element and zero element do not need to participate in verification.
The complexity of verification may be simplified by analyzing the nature of specific operations.

Basic concepts of algebraic systems

The concept of algebraic system

X is a non-empty set, X and m operations on X, f1, f2,...fm constitute an algebraic system U, denoted as U=<X, f1,f2...fm.> (m>=1)

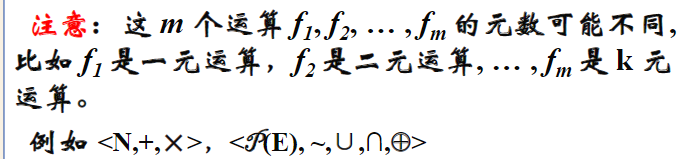
U=<X, f1, f2,..., fm> is an algebraic system. If X is a finite set, then U is called a finite algebraic system.
Given two algebraic systems U=<X, f,fz…,.fm>,V=<Y, g1,g2…,gm>, if the corresponding operations fi and gi have the same element number (i=1,2 ,3,...m), it is said that U and V are the same type of algebraic system.

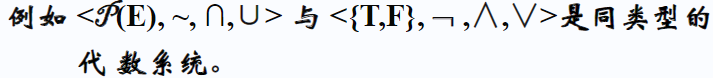
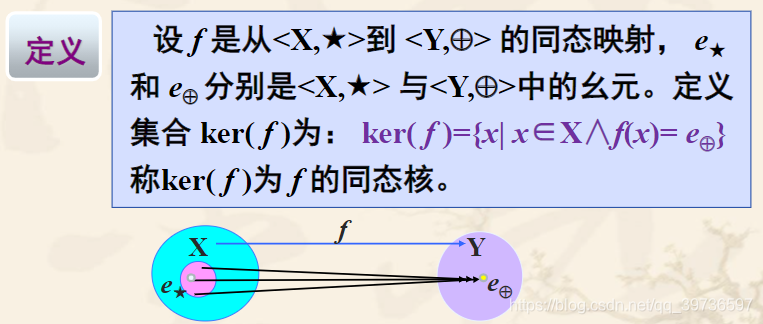
Homomorphism and Isomorphism of Algebraic Systems

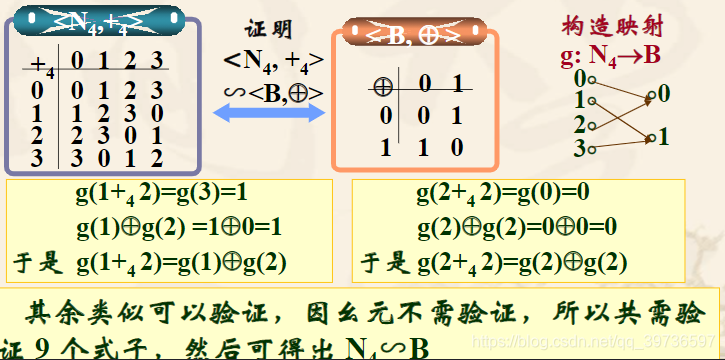
Observe the following two algebra systems,

R is the set of real numbers, R+ is the set of real numbers greater than 0, and X and + are ordinary real number multiplication and addition operations. On the surface, these two algebraic systems are completely different, but in fact, the properties of their operations are exactly the same, both satisfying: commutative, associative, unitary, and reversible for each element.
How can we see that they have the same properties?


Note: The homomorphism must be a mapping. This mapping involves two algebraic systems. It is a mapping from X to Y and must satisfy a homomorphic relationship.
If f is surjective, we call this homomorphism a full homomorphism.
If f is incident, the homomorphism is called a single homomorphism.
If f is bijective, the homomorphism is said to be isomorphism, denoted as X≌Y.
If f is a homomorphism (isomorphism) from <X,★> to <X,★>, it is called an automorphism (automorphism).




Note: The necessary conditions for the algebraic system <X,★> and <Y,o> to be isomorphic:

1. The bases of X and Y are the same, that is, K[X]=K[Y].
2. Transport operator ★ and o are the same type.
3. There exists a bijection f:X→Y, and it satisfies the isomorphism relation .

Not all bijectives f:X->Y satisfy the isomorphism relation .
When constructing bijection, we should pay attention to:
unitary element corresponds to unitary element; zero element corresponds to zero element;
inverse element also corresponds to each other.

Isomorphism of an algebraic system with two operations

The isomorphic relationship between algebraic systems ≌ is an equivalence relationship .
When proving, we have to consider what is the equivalence relationship, the relationship satisfies reflexivity, symmetry, and transit. Then prove that the isomorphic relationship is reflexive, symmetrical, and transitive.

The properties of isomorphism in algebraic systems

For two isomorphic algebraic systems, some operational properties are preserved.
That is, some operational properties in <X,★> are also in <Y,o>, and vice versa.

Maintain combinability

1) If the operation ★ can be combined in X, then o can also be combined in Y.

Maintain exchangeability

2) If the operation ★ can be exchanged in X, then o can also be exchanged in Y.
The method of proof is similar to 1). Prove it by yourself.

Keep unitary existence

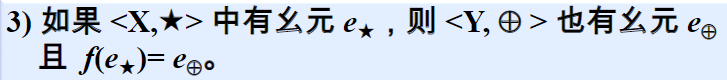
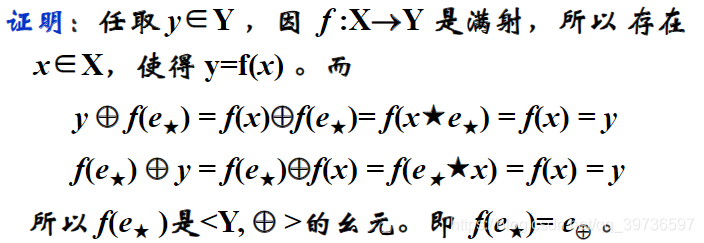
Keep zero element existence

Maintain the existence of inverse elements

Keep the law of distribution

Keep the law of absorption

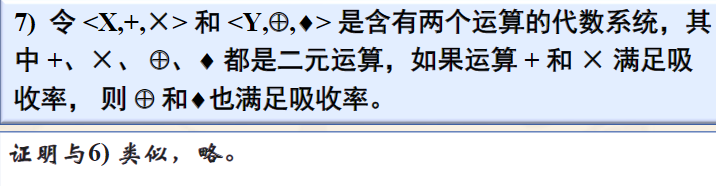
The preservation of isomorphic properties is bidirectional, that is, the properties of operations in Y can also be maintained in operations in X.
Since the homomorphism relationship does not satisfy symmetry, the maintenance of the homomorphism property is only one-way. That is, the nature of ○ in Y, and ★ in X may not have.

The properties of isomorphism in algebraic systems