图解二叉搜索树（C++）

二叉搜索树

定义
二叉搜索树（二叉排序树）可以是一颗空树（无结点）
也可以：
若它的左子树不空，则左子树上的所有结点都小于其根节点的值
若它的右子树不空，则右子树上的所有结点都大于其根节点的值
它的左右子树分别也必须是二叉搜索树
如图：

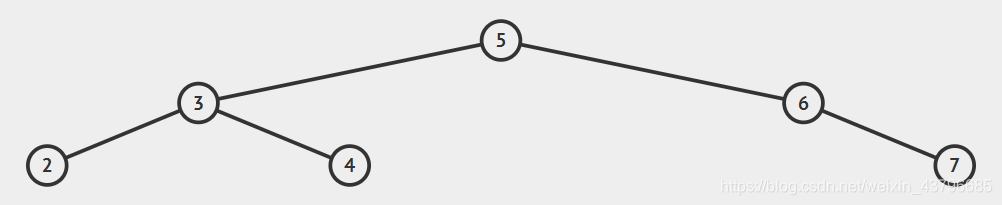
最左边的值一定是最小值，最右边的值一定是最大值

结点结构

template<class T>  //模板参数
struct BSTNode
{
	BSTNode(const T& data = T()) //初识化时先将其指针都置空
	:_data(data)
	, _pLeft(nullptr)
	, _pRight(nullptr)
	{}

	T _data;
	BSTNode<T>* _pLeft; //左孩子指针
	BSTNode<T>* _pRight; //右孩子指针
};

插入操作

第一种情况：该树为空树

直接申请pRoot结点，将data的值放入Root结点中

第二种情况：该树不为空

定义pParent、pCur结点，用pCur结点进行向下遍历（遍历条件：data的值比pCur->data的值大，pCur向右孩子遍历，否则，pCur向左孩子遍历，pParent紧随其后）

	bool Insert(const T& data)
	{
		//空树
		if (_pRoot == nullptr)
		{
			_pRoot = new Node(data);
			return true;
		}
		//按照二叉搜索树性质找当前接结点的位置
		Node* pCur = _pRoot;
		Node* pParent = nullptr;
		while (pCur)
		{
			pParent = pCur;
			if (data < pCur->_data)
				pCur = pCur->_pLeft;
			else if (data > pCur->_data)
				pCur = pCur->_pRight;
			else
				return false;
		}
		//进行插入
		pCur = new Node(data);
		if (data < pParent->_data)
			pParent->_pLeft = pCur;
		else
			pParent->_pRight = pCur;
		return true;
	}

删除操作

第一种情况：删除叶子结点（删除存在两个空结点的树）

直接删除即可。

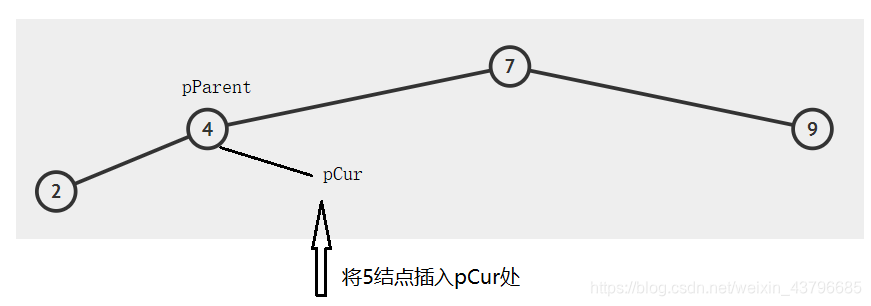
第二种情况：删除只有一个孩子的结点（删除存在一个空结点的树）

直接将该结点删除，并且将该节点的父节点指向下一个结点。需要分只存在左孩子的情况和只存在有孩子的情况。
第一种情况可以归并在第二种情况内

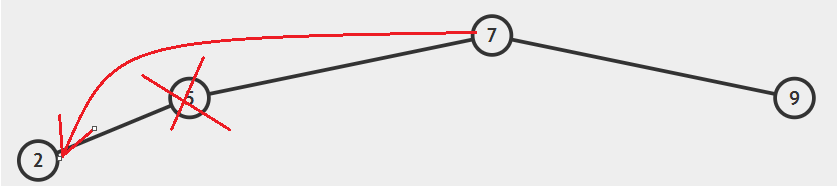
第三种情况：删除有两个孩子的结点

需要找一个替换结点。
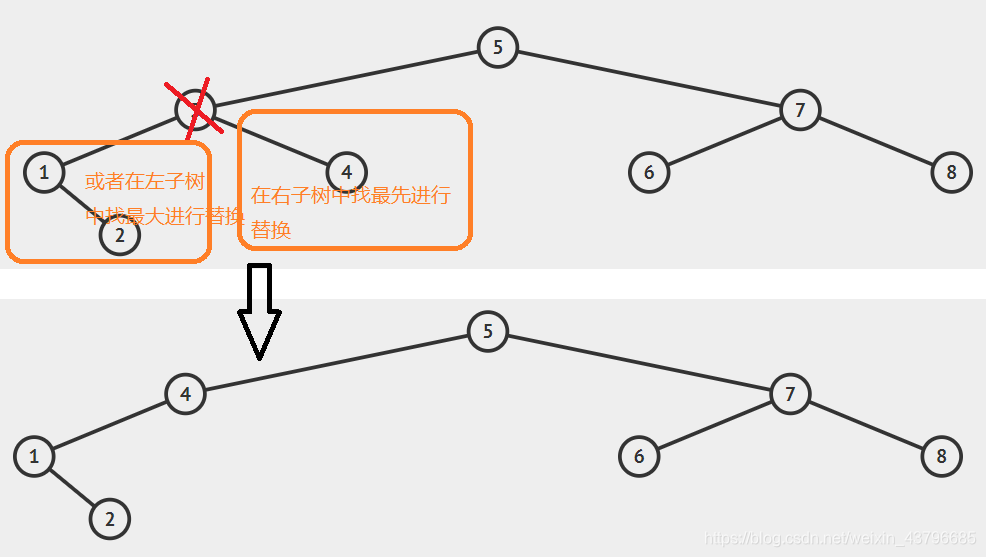
替换结点可以是在左子树中找最大的结点，或者为在右子树中找最小的结点，下图为在右子树中找最小结点进行替换，在删除指定结点，然后更改一些指针的指向

最后，共两种情况，代码如下：

//删除结点
/*1.叶子结点---直接删除
  2.只有左孩子||只有右孩子（叶子节点可以合并于此）---直接删除
  3.左右孩子都村在---找一个替代节点（该结点的左子树中最大或者右子树中最小）
*/
bool Delete(const T& data)
{
	//空树，直接返回
	if (_pRoot == nullptr)
		return false;
	Node* pCur = _pRoot;
	Node* pParent = nullptr;
	//找待删除结点pCur
	while (pCur)
	{
		if (data == pCur->_data)
			break;
		else if (data < pCur->_data)
		{
			pParent = pCur;
			pCur = pCur->_pLeft;
		}
		else
		{
			pParent = pCur;
			pCur = pCur->_pRight;
		}
	}
		//pCur只有右孩子
	if (nullptr == pCur->_pLeft)
	{
		//根节点
		if (pCur == _pRoot)
			_pRoot = pCur->_pRight;

			//待删除结点在父节点的左边还是右边
		else
		{
			if (pParent->_pLeft == pCur)
				pParent->_pLeft = pCur->_pRight;
			else
				pParent->_pRight = pCur->_pRight;
		}
	}
	else if (nullptr == pCur->_pRight) //pCur只有左孩子
	{
		if (pCur == _pRoot)
			_pRoot = pCur->_pLeft;
		else
		{
			if (pParent->_pLeft == pCur)
				pParent->_pLeft = pCur->_pLeft;
			else
				pParent->_pRight = pCur->_pLeft;
		}
	}
	else     //左右孩子都有
	{
		//找右边最左边的结点进行替换
		Node* pRSwap = pCur->_pRight;
		pParent = pCur;
			while (pRSwap->_pLeft)
		{
			pParent = pRSwap;
			pRSwap = pRSwap->_pLeft;
		}
		pCur->_data = pRSwap->_data;
		//将pSwap右边的树与pParent结点连接
		if (pRSwap == pParent->_pLeft)
			pParent->_pLeft = pRSwap->_pRight;
		else
			pParent->_pRight = pRSwap->_pRight;
			pCur = pRSwap;
	}

查找操作

查找操作和删除操作时的找到指定结点相同，直接使用比较的方法进行遍历就可以。

Node* Find(const T& data) const
{
	Node* pCur = _pRoot;
	while (pCur)
	{
		if (data == pCur->_data)
			return pCur;
		else if (data < pCur->_data)
			pCur = pCur->_pLeft;
		else
			pCur = pCur->_pRight;
	}
	return nullptr;
}

取最大最小值

最小值：存放在二叉搜索树的最左端
最大值：存放在二叉搜索树的最右端

Node* LeftMost() const
{
	if (nullptr == _pRoot)
		return nullptr;
	Node* pCur = _pRoot;
	while (pCur->_pLeft)
		pCur = pCur->_pLeft;
	return pCur;
}

Node* RightMost() const
{
	if (nullptr == _pRoot)
		return nullptr;
	Node* pCur = _pRoot;
	while (pCur->_pRight)
		pCur = pCur->_pRight;
	return pCur;
}

遍历操作

前序遍历：先遍历根节点，在遍历左子树，在遍历右子树
中序遍历：先遍历左子树，在遍历根节点，在遍历右子树
中序遍历：可以打印出升序的二叉搜索树
后序遍历：一边完成二叉搜索树的销毁操作
中序遍历代码：

void _InOrder(Node* _pRoot)
{
	if (_pRoot)
	{
		_InOrder(_pRoot->_pLeft);
		cout << _pRoot->_data << " ";
		_InOrder(_pRoot->_pRight);
	}
}

销毁清空

使用后序遍历的方式销毁二叉搜索树，这样可以使释放结点更为有序，从而达到不漏，不重的销毁工作。

void _Destroy(Node*& _pRoot)
{
	if (_pRoot)
	{
		_Destroy(_pRoot->_pLeft);
		_Destroy(_pRoot->_pRight);
		delete _pRoot;
	}
}

总结

• 插入和删除操作都必须按照查找的方式找到需要操作的位置，这样查找的性能也就代表了插入和删除的性能。
• 二叉树的的结点越深，查找的循环次数越多。
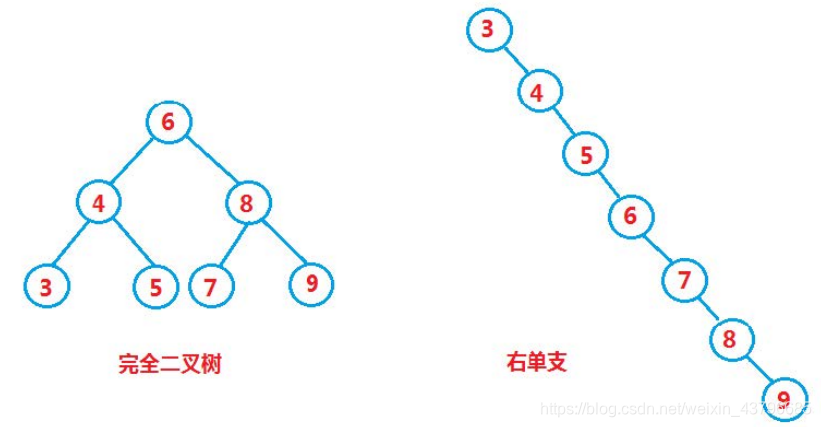
• 对于插入的顺序也会影响到二叉搜索树的结构，同样二叉搜索树的结构不同，也就影响着二叉树的查找效率。如下图所示：插入{6，4，5，8，3，5，7，9} 与 插入{3，4，5，6，7，8，9} 的二叉搜索树结构不同。