二叉搜索树
- 概念
- 实现
  - 数据结构
  - 初始化
  - 构建新结点
  - 插入
  - 查找
  - 删除
    - 查找前驱/后继
    - 删除
- 完整代码
  - 题目
  - 代码

二叉搜索树

二叉搜索树/排序二叉树/二叉查找树都是一样的。

概念

二叉搜索树满足这样一个性质：
每个结点有一个关键字 $key$ 。
对于结点 $a$ ，它左子树里面所有结点的 $key<a.key$ ，右子树里面所有结点的 $key \geq a.key$ （当然，反过来也无妨）。
注意：是“子树”，而不只是“儿子”满足这个条件。

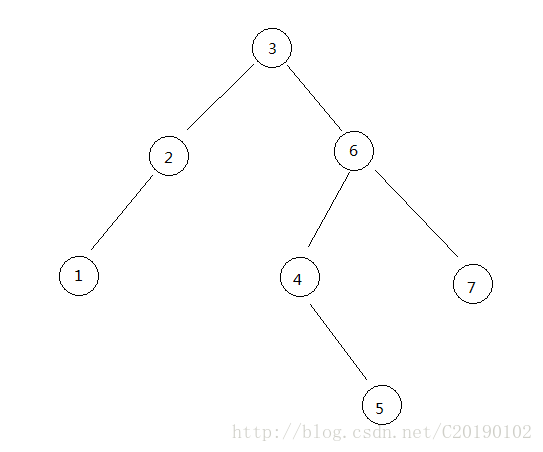
例如，这就是一棵二叉搜索树：
二叉搜索树示例

二叉搜索树的中序遍历一定是一个有序序列。

实现

下面是构造一个，满足对于结点 $a$ ，它左子树里面所有结点的 $key<a.key$ ，右子树里面所有结点的 $key \geq a.key$ 的二叉搜索树。

数据结构

我们用指针（链表）。
或许你听到这个词后会直接关闭这个博客的页面，但我会尽量把它讲清楚。

如果不嫌弃，这篇关于指针的博客还是有点点用：C++指针详解

如果你不想看，在代码中我会有注释。

#define MAXN 500000
struct node
{
    int key;//关键字
    node *ch[2],*fa;//指向左儿子(ch[0])、右儿子(ch[1])和父亲(fa)
};
node tree[MAXN+5];//树
node *Root,*NIL,*ncnt;
//Root: 指向根的位置
//NIL:  模拟空指针（C++其实有自带的“空”：NULL，但是这个会有用的）
//ncnt: 指向最后一个插入的结点
//看不懂没关系，后面就知道了

初始化

void Init()
{
    NIL=&tree[0];
    NIL->fa=NIL->ch[0]=NIL->ch[1]=NIL;
    //把NIL指向一个不会用到的结点，就是我们自定义的“空”
    ncnt=&tree[0];
    Root=NIL;
}

构建新结点

//由于这个须多次调用，加上inline可以快一点
inline node *NewNode(int val)//val: 要构建的结点的关键字
{
    node *p=++ncnt;//p就指向新的结点

    //把最后插入的结点的位置后移一位
    //实际上，在数组中每个元素的位置是连续的
    //例如，当ncnt指向tree[1]时，++ncnt
    //那么ncnt就指向了tree[2]

    p->key=val;//保存关键字

    //一个结构体指针，要访问它指向的结构体的元素，用"->"即可

    p->fa=p->ch[0]=p->ch[1]=NIL;//初始化亲戚关系
    return p;//返回这个结点指针
}

插入

void Insert(node *&rt,node *fa,int val)
//rt:  当前结点
//fa:  当前结点的父亲
//（因为NIL的父亲是没有的，在新建结点时无法初始化这个结点的父亲，所以要把fa作为一个参数）
//val: 要插入的关键字
{
    if(rt==NIL)                  //当前结点为空 => 插入到这里
    {
        rt=NewNode(val);         //新结点
        rt->fa=fa;               //父亲修改
        return;
    }
    int d=val>=rt->key;          //d就表示了要找左子树还是右子树
    Insert(rt->ch[d],rt,val);
}

这是一个插入示例：

扫描二维码关注公众号，回复： 3768112 查看本文章

查找

//用于查找关键字为val的结点，返回它的地址
node *Find(node *rt,int val)
{
    if(rt==NIL) return NIL;      //找到空节点 => 没有结点的关键字为val => 返回空指针
    if(rt->key==val) return rt;  //找到了 => 返回该结点指针
    int d=val>=rt->key;          //和插入一样
    return Find(rt->ch[d],val);
}

实际上查找和插入差不多，就不过多解释了。

删除

查找前驱/后继

由于删除需要用到，所以先说这个。

我这个二叉搜索树中，
一个结点的后继（比它大的最小的一个）一定是这个结点的左子树中的最右边的一个。
前驱（比它小的最大的一个）一定是它右子树中最左边的一个。

node *FindNext(node *rt)
{
    if(rt==NIL) return NIL;//这句用于预防查找后继的结点为空
    node *y=rt->ch[1];
    //注意当rt为叶子结点的话，它的ch[1]还没有，但是由于之前我们自定义了一个“空”，而它并不是真正的空，就避免了这个问题
    while(y->ch[0]!=NIL)
        y=y->ch[0];
    return y;
}

不知道你有没有发现一个问题，如果是这个树：
后继示例
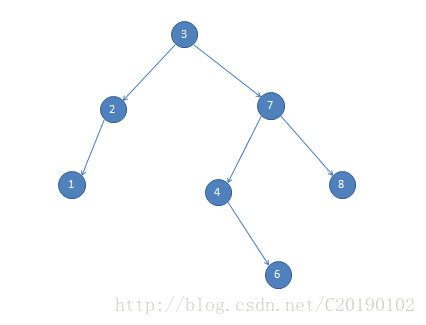
我们想找1的后继，显然上面的函数会返回NIL（1没有儿子）。
但严格上来说1的后继是2。
但就二叉搜索树来说，一个结点的后继就是它右子树中最左边的一个。
这种情况就很恶心了，但是删除中不会出现这个问题，所以先不管他。

前驱是一样的：

node *FindLast(node *rt)
{
    if(rt==NIL) return NIL;
    node *y=rt->ch[0];
    while(y->ch[1]!=NIL)
        y=y->ch[1];
    return y;
}

删除

这个有必要详细说一下。

如果要删的结点 $rt$ 是叶子结点，好办，直接删掉即可。
如果要删的结点 $rt$ 只有一个儿子，也好办，把这个儿子接在 $rt$ -> $fa$ 上即可。

注意，这里的“删”不是真的在内存中把它删掉，而是把它孤离出来，这样可以使这个结点不被访问到，也就达到了删除的目的。

例如：
删除-1
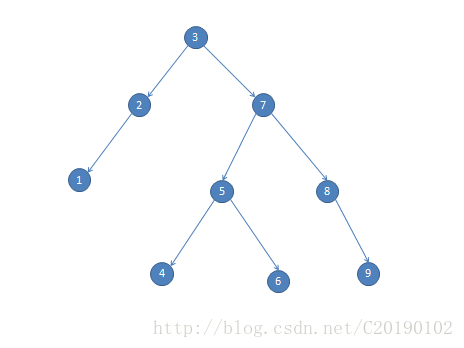
如果要删1、4、6或9，把它和它父亲之间的边去掉就可以了。
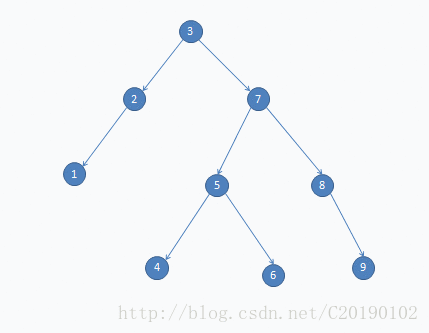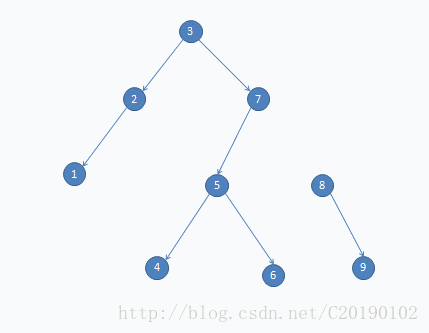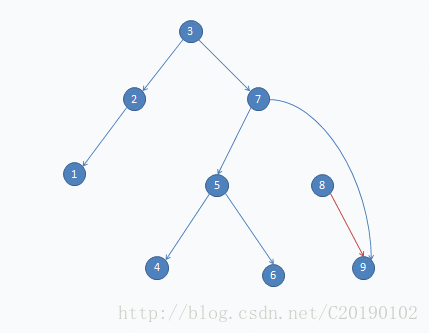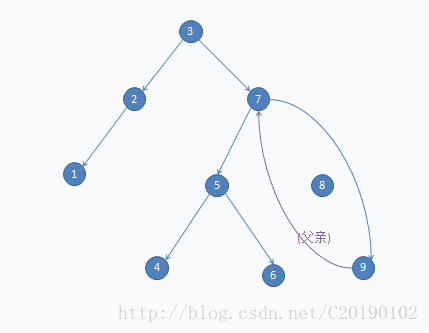
如果要删8：
删除-2

还有一种情况： $rt$ 有2个儿子（例如上图中的7）。显然需要找一个和7最接近的一个结点（前驱或后继去替换它）。否则，例如选5去替换7，左子树中就有一个6比5大，不符合二叉搜索树的条件（而且用5去替换7很难实现）。反之，选6，左子树的结点全部比它小，右子树的结点全部比它大，而且6是叶子结点（事实上一个结点的后继或前驱一定是叶子结点），很好实现。

由于我做的这道题不是Special Judge，要求删除结点是用后继替换（用前驱还是用后继替换会决定删除结点后你的树的样子），所以我就用了后继进行替换。
替换结点时只需要替换 $rt$ 的 $key$ ，然后删除 $rt$ 的后继即可。

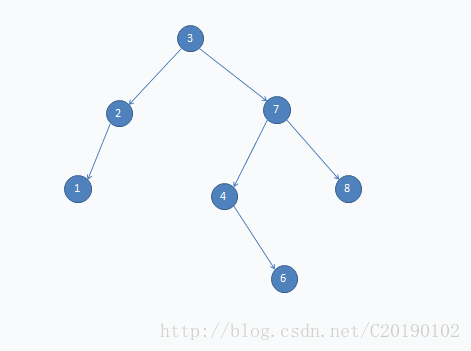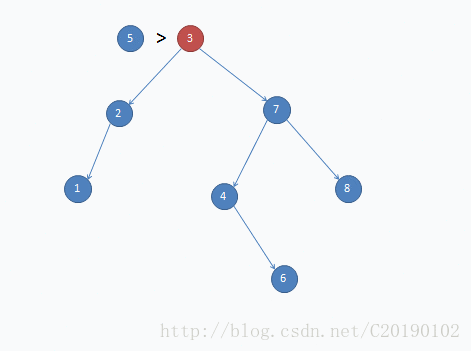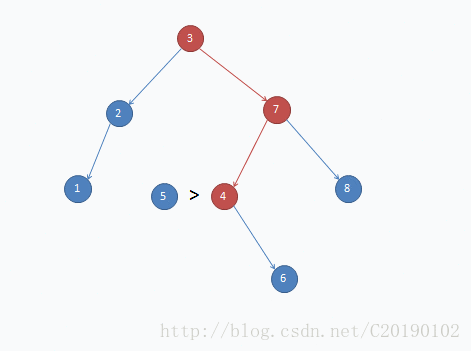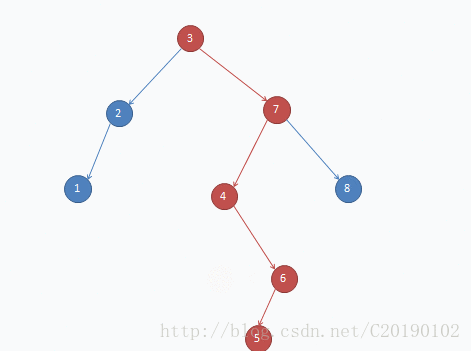
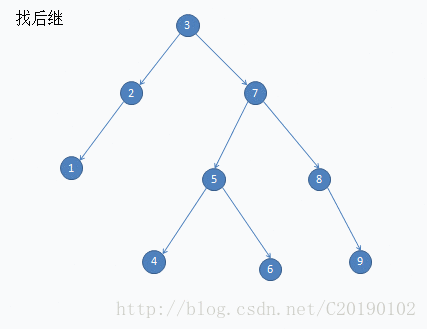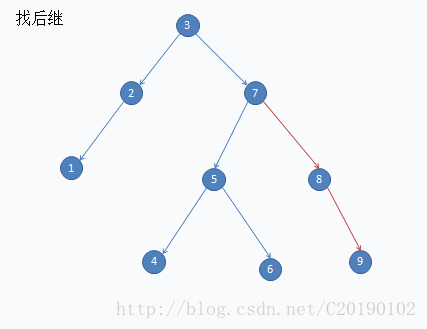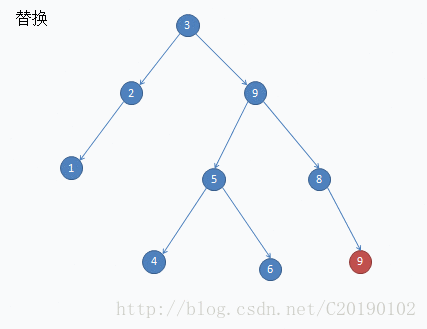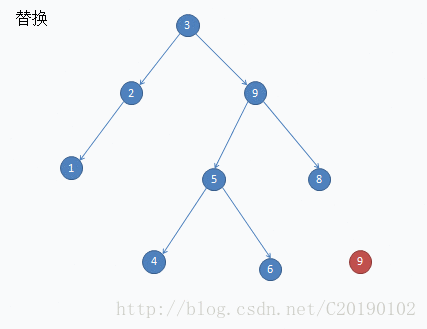
这是删除7的例子：
删除-3

void Delete(node *rt,int val)
//rt:  根
//val: 要删的结点的关键字
{
    node *x,*y,*z=Find(rt,val);//把想删的结点找到
    //x: 真正要删的结点的儿子（真正要删的结点最多有1个儿子）
    //y: 真正要删的结点
    //z: 想删的结点
    if(z==NIL)//没有这个结点
        return;
    if(z->ch[0]==NIL||z->ch[1]==NIL)//z的儿子个数小于2
        y=z;//直接删z
    else
        y=FindNext(z);//删z的后继
    if(y->ch[0]!=NIL)
        x=y->ch[0];
    else
        x=y->ch[1];
    //看y有哪个儿子（或者没有儿子）
    if(x!=NIL)//y有儿子
        x->fa=y->fa;//更新y的儿子的父亲
    if(y->fa==NIL)//y是根
        Root=x;//更新根
    else
    {
        int d=y==y->fa->ch[1];//看y是左儿子还是右儿子
        y->fa->ch[d]=x;
    }
    if(y!=z)
        z->key=y->key;//直接更新z的key
}

完整代码

题目

Binary Search Tree III
这道题有4个操作：

插入一个数
删除一个数
查找树中有没有一个数
输出树的中序遍历和先序遍历（所以删除时必须用后继替换，否则先序遍历就不一样了）

代码

#include<cstdio>
#define MAXN 500000

struct node
{
    int key;
    node *ch[2],*fa;
};
node tree[MAXN+5];
node *Root,*NIL,*ncnt;

void Init()
{
    NIL=&tree[0];
    NIL->fa=NIL->ch[0]=NIL->ch[1]=NIL;
    ncnt=&tree[0];
    Root=NIL;
}

inline node *NewNode(int val)
{
    node *p=++ncnt;
    p->key=val;
    p->fa=p->ch[0]=p->ch[1]=NIL;
    return p;
}

void Insert(node *&rt,node *fa,int val)
{
    if(rt==NIL)
    {
        rt=NewNode(val);
        rt->fa=fa;
        return;
    }
    int d=val>=rt->key;
    Insert(rt->ch[d],rt,val);
}

node *Find(node *rt,int val)
{
    if(rt==NIL) return NIL;
    if(rt->key==val) return rt;
    int d=val>=rt->key;
    return Find(rt->ch[d],val);
}

node *FindNext(node *rt)
{
    if(rt==NIL) return NIL;
    node *y=rt->ch[1];
    while(y->ch[0]!=NIL)
        y=y->ch[0];
    return y;
}

void Delete(node *rt,int val)
{
    node *x,*y,*z=Find(rt,val);
    if(z==NIL) return;
    if(z->ch[0]==NIL||z->ch[1]==NIL) y=z;
    else y=FindNext(z);
    if(y->ch[0]!=NIL) x=y->ch[0];
    else x=y->ch[1];
    if(x!=NIL) x->fa=y->fa;
    if(y->fa==NIL) Root=x;
    else
    {
        int d=y==y->fa->ch[1];
        y->fa->ch[d]=x;
    }
    if(y!=z) z->key=y->key;
}

void InOrder(node *rt)
{
    if(rt==NIL) return;
    InOrder(rt->ch[0]);
    printf(" %d",rt->key);
    InOrder(rt->ch[1]);
}
void PreOrder(node *rt)
{
    if(rt==NIL) return;
    printf(" %d",rt->key);
    PreOrder(rt->ch[0]);
    PreOrder(rt->ch[1]);
}

int main()
{
    int N;
    Init();
    scanf("%d",&N);
    for(int i=1;i<=N;i++)
    {
        int x;char opt[10];
        scanf("%s",opt);
        if(opt[0]=='i')
        {
            scanf("%d",&x);
            Insert(Root,NIL,x);
        }
        else if(opt[0]=='f')
        {
            scanf("%d",&x);
            node *pos=Find(Root,x);
            if(pos==NIL) printf("no\n");
            else printf("yes\n");
        }
        else if(opt[0]=='d')
        {
            scanf("%d",&x);
            Delete(Root,x);
        }
        else
        {
            InOrder(Root);puts("");
            PreOrder(Root);puts("");
        }
    }
}

C++二叉搜索树动图详解

二叉搜索树

概念

实现

数据结构

初始化

构建新结点

插入

查找

删除

查找前驱/后继

删除

完整代码

题目

代码

猜你喜欢