排序——选择排序（简单选择排序、堆排序）

这是排序部分的第二篇文章，其他的排序方法可以点击下面的传送门(•͈ᴗ•͈ૢૢ)❊⿻*

排序算法合辑

文章目录

简单选择排序（simple selection sort）

排序过程
代码
算法分析
实例

堆排序（heap sort）

排序过程
代码
算法分析
实例

简单选择排序（simple selection sort）

基本思想是第i趟排序从待排序序列中找到最小值，并和第i个记录交换，作为有序序列的第i个记录。

排序过程

将整个记录序列划分为有序区和无序区，初始时有序区为空，无序区含有待排序的所有记录。
在无序区中选取关键码最小的记录，将它与无序区中的第一个记录交换，使得有序区扩展了一个记录，同时无序区减少了一个记录。
不断重复2，直到无序区只剩下一个记录为止。此时所有的记录已经按关键码从小到大的顺序排列。

例如待排序序列12,5,19,35,3
在这里插入图片描述
从例子中可以看出每次排序，有序区的记录最终位置已经确定。

代码

void SelectSort(int a[],int n)
{
	for (int i=0;i<n-1;i++)
	{
		int index=i;
		for(int j=i+1;j<n;j++)
		{
			if (a[j]<a[index]) 
				index=j;
		}
		if (index!=i)
		{
			int mid=a[i];
			a[i]=a[index];
			a[index]=mid;
		}
	}
}

算法分析

/	时间复杂度	空间复杂度
最好情况	$O(n^2)$
最坏情况	$O(n^2)$
平均	$O(n^2)$	$O(1 )$

实例

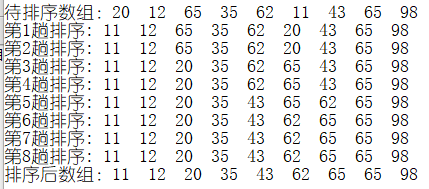
在这里插入图片描述

#include <iostream>
using namespace std;
void print (int a[],int n)
{
	for (int i=0;i<n;i++)
		cout<<a[i]<<"  ";
	cout<<endl;
} 
void SelectSort(int a[],int n)
{
	for (int i=0;i<n-1;i++)
	{
		int index=i;
		for(int j=i+1;j<n;j++)
		{
			if (a[j]<a[index]) 
				index=j;
		}
		if (index!=i)
		{
			int mid=a[i];
			a[i]=a[index];
			a[index]=mid;
		}
		/*-------------排序过程--------------*/
		cout<<"第"<<i+1<<"趟排序: "; 
		print(a,n);
	}
}
int main()
{
	int a[9]={20,12,65,35,62,11,43,65,98};
	cout<<"待排序数组：";
	print(a,9);
	SelectSort(a,9);
	cout<<"排序后数组：";
	print(a,9);
	return 0;
}

堆排序（heap sort）

堆排序是简单选择排序的改进，是利用堆的特性进行排序的方法。基本思想是（假设用大根堆）首先将待排序的记录序列构造成一个堆，选出堆中所有记录的最大者即堆顶的记录，然后将堆顶记录移走，并将剩余记录再调整成堆，这样又能找出一个当前最大的记录，以此类推，直到堆中只有一个记录为止。

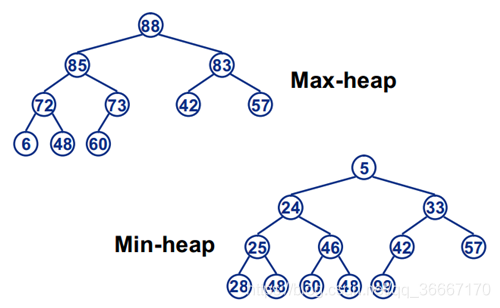
什么是堆？
堆（heap） 是具有下列性质的完全二叉树：每个结点的值都小于或等于其左右孩子结点的值（称为小根堆）；或者每个结点的值都大于或等于其左右孩子结点的值（称为大根堆）。顺序存储结构表示就是：
$小根堆\begin{cases} k_i \leq k_{2i}\\ k_i \leq k_{2i+1} \end{cases} 1 \leq i \leq \lfloor n/2 \rfloor$
$大根堆\begin{cases} k_i \geq k_{2i}\\ k_i \geq k_{2i+1} \end{cases} 1 \leq i \leq \lfloor n/2 \rfloor$

排序过程

将一个无序序列构造成一个堆，即初始建堆
数据用顺序存储结构存储，将所有的数据都放在一个数组中，这就可以看成是一个完全二叉树的顺序存储结构。 接下来就只需要把它调整成一个堆即可。
处理堆顶记录：建好堆之后将待排序序列分为无序区和有序区两部分，其中无序区为堆，包括全部待排序记录，有序区是空的。将堆顶与堆中最后一个记录交换，则堆（无序区）中少了一记录，有序区增加一个记录。
调整剩余记录成一个新的堆

如何把完全二叉树调整成堆？
以大根堆为例，堆的定义可以知道大根堆是双亲结点的值大于其左右孩子的节点，所以说在大根堆的调整过程中总是将根节点和左右孩子进行比较，若不满足堆的条件，则将根节点与左孩子或右孩子的较大者进行交换，这个调整过程一直进行到所有子树均为堆，或者被调整节点交换到叶子节点为止。
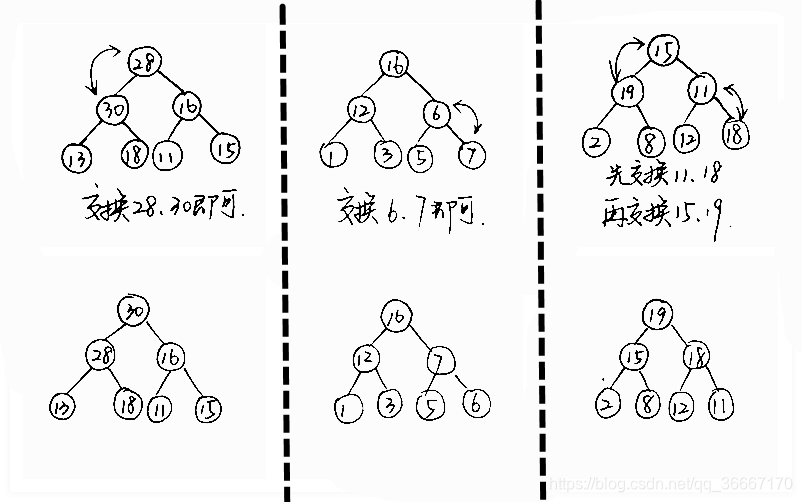
在这里插入图片描述
因为数据是存储在数组中的，由完全二叉树的定义可以知道，有n个结点的完全二叉树，最后一个双亲结点(最后一个叶子结点的双亲) 的位置是 $\lfloor n/2 \rfloor$ ，则在数组中，只需要从 $k= \lfloor n/2 \rfloor$ 位置开始，与其位置为 $2k$ 和 $2k+1$ 的孩子结点比较，然后逐个向前调整，一直调整到第一个记录。
再举个栗子，排序过程，待排序序列36,30,18,40,32,45,22,50
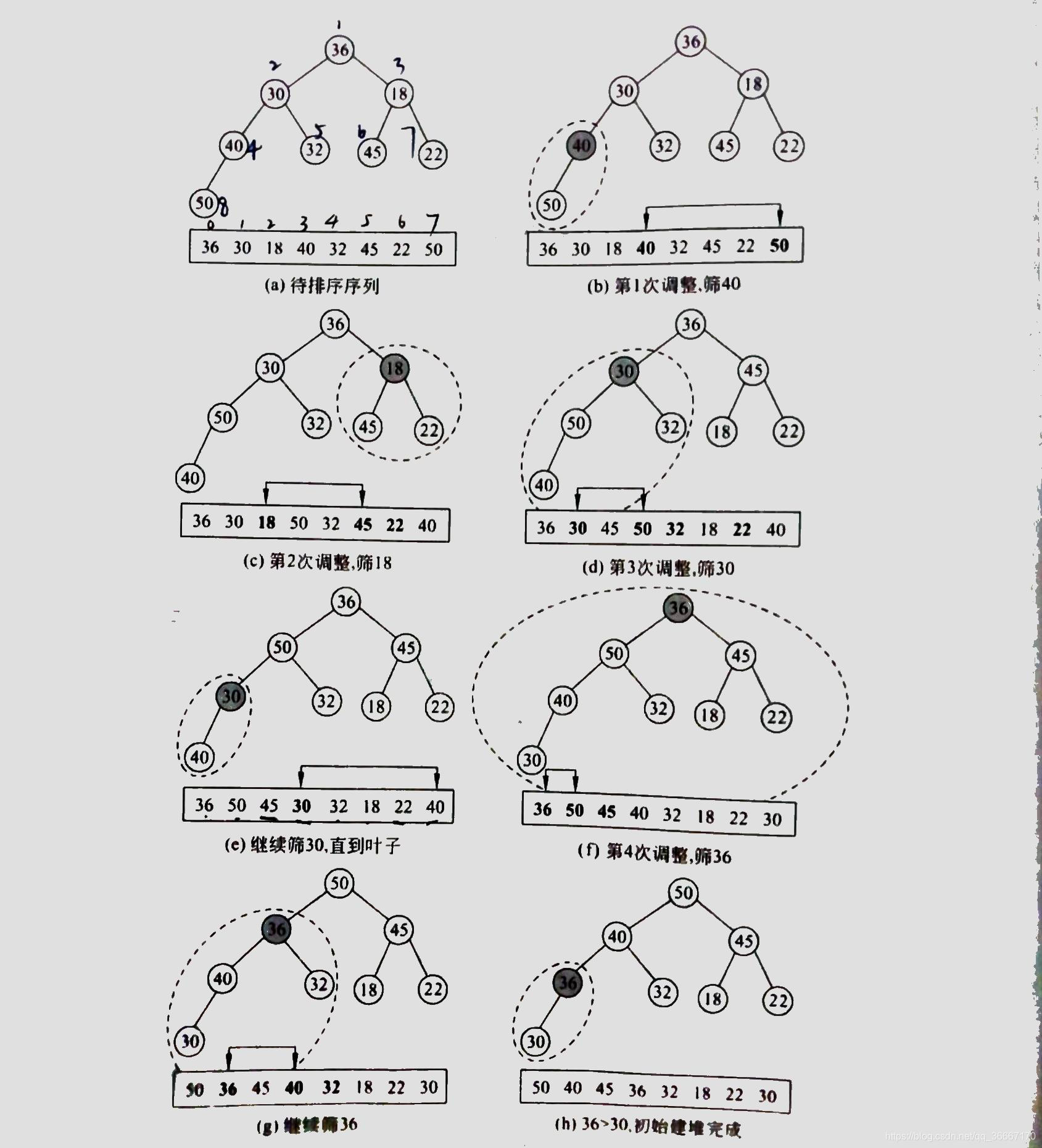
在这里插入图片描述
……后边步骤不放了，应该能自己知道。具体代码看最后实例部分。

代码

写法一
直接就这么写，从数组0号位开始，计算 $k$ 的孩子结点就不能用 $2k$ 和 $2k+1$ ，而应该在这个基础上+1。（因为根结点在a[0]， $0*2=0，0*2+1=1$ ，但是a[0]的孩子结点应的a[1]a[2]）

void sift(int a[],int low,int high)
{
	int i=low,j=2*i+1;//i为待调整结点，j为其左孩子,注意数组是0开始的，所以左孩子在2*i+1的位置
	while(j<=high) //必须有=，保证剩两个结点时能进行堆重构
	{
		if (j<high && a[j]<a[j+1]) //比较左右孩子，选出较大者 
			j++;
		if(a[i]>=a[j])//符合堆条件 
			break;
		else//不符合堆的条件，进行调整 
		{
			swap(a[i],a[j]);
			i=j;
			j=2*i+1;
		}
	}
}
void HeapSort(int a[],int n)
{
	n--; //堆的第一个记录在数组的0号位，最后一个记录在数组的n-1号位 
	for(int i=n/2;i>=0;i--)//从n/2开始调整 
		sift(a,i,n);
	for (int i=0;i<n;i++)
		/*开始传入参数n为数组长度8，HeapSort中进行n--，此时n=7，
		进行7趟即可，最后只剩一个根节点时自动并入有序区*/
	{
		swap(a[0],a[n-i]);//将第一个与堆中最后一个交换
		sift(a,0,n-i-1);//此时堆就减少一个
	}
}

写法二
浪费一个数组空间a[0]，从a[1]开始存储数据。个人感觉这样写比较简单（其实没差别( ‘-ωก̀ )）。

void sift(int a[],int low,int high)
{
	int i=low,j=i*2;
	while(j<=high) 
	{
		if (j<high && a[j]<a[j+1]) 
			j++;
		if(a[i]>=a[j])
			break;
		else
		{
			swap(a[i],a[j]);
			i=j;
			j=2*i;
		}
	}
}
void HeapSort(int a[],int n)
{
	for(int i=n/2;i>=1;i--)
		sift(a,i,n);
	for (int i=1;i<n;i++)
	{
		swap(a[1],a[n-i+1]);
		sift(a,1,n-i);
	}
}

算法分析

/	时间复杂度	空间复杂度
最好情况	$O(nlog_2 n)$
最坏情况	$O(nlog_2 n)$
平均	$O(nlog_2 n)$	$O(1 )$

实例

在这里插入图片描述
写法一

#include <iostream>
using namespace std;
void print(int a[],int n)
{
	for (int i=0;i<n;i++) 	
		cout<<a[i]<<"  ";
	cout<<endl;
} 
void sift(int a[],int low,int high)
{
	int i=low,j=2*i+1;					//i为待调整结点，j为其左孩子
										//数组是0开始的，所以左孩子在2*i+1的位置
	while(j<=high) 						//必须有=，保证剩两个结点时能进行堆重构
	{
		if (j<high && a[j]<a[j+1]) 		//比较左右孩子，选出较大者 
			j++;
		if(a[i]>=a[j])					//符合堆条件 
			break;
		else							//不符合堆的条件，进行调整 
		{
			swap(a[i],a[j]);
			i=j;
			j=2*i+1;
		}
	}
}
void HeapSort(int a[],int n)
{
	n--; 								//堆的第一个记录在数组的0号位
										//最后一个记录在数组的n-1号位 
	for(int i=n/2;i>=0;i--)				//从n/2开始调整 
		sift(a,i,n);

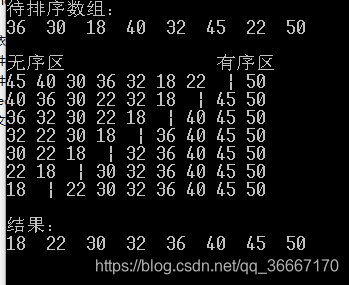
	cout<<"无序区               有序区"<<endl;
	for (int i=0;i<n;i++)
		/*开始传入参数n为数组长度8，HeapSort中进行n--，此时n=7，
		进行7趟即可，最后只剩一个根节点时自动并入有序区*/
	{
		swap(a[0],a[n-i]);				//将第一个与堆中最后一个交换
		sift(a,0,n-i-1);				//此时堆就减少一个
		/*-----------输出过程-----------*/
		for (int j=0;j<n-i;j++)
			cout<<a[j]<<" ";
		cout<<" | ";
		for (int j=n-i;j<=n;j++)
			cout<<a[j]<<" ";
		cout<<endl;
	}
}
int main()
{
	int a[8]={36,30,18,40,32,45,22,50};
	cout<<"待排序数组："<<endl;
	print(a,8);
	HeapSort(a,8);
	cout<<"排序结果："<<endl;
	print(a,8);
	return 0;
}

写法二

#include <iostream>
using namespace std;
void print(int a[],int n)
{
	for (int i=1;i<=n;i++) 
		cout<<a[i]<<"  ";
	cout<<endl;
} 
void sift(int a[],int low,int high)
{
	int i=low,j=i*2;
	while(j<=high) 
	{
		if (j<high && a[j]<a[j+1]) 
			j++;
		if(a[i]>=a[j])
			break;
		else
		{
			swap(a[i],a[j]);
			i=j;
			j=2*i;
		}
	}
}
void HeapSort(int a[],int n)
{
	for(int i=n/2;i>=1;i--)
		sift(a,i,n);
	for (int i=1;i<n;i++)
	{
		swap(a[1],a[n-i+1]);
		sift(a,1,n-i);
	}
}
int main()
{
	int a[9]={0,36,30,18,40,32,45,22,50};
	cout<<"待排序数组："<<endl;
	print(a,8);
	cout<<endl;
	cout<<"HeapSort:"<<endl;
	HeapSort(a,8);
	print(a,8);
	cout<<endl;
	return 0;
}

LolitaSian

发布了107 篇原创文章 · 获赞 402 · 访问量 50万+

私信关注