update:退役后对这篇文章进行了一些更新,主要增加了一个后缀平衡树的版块。很遗憾的,csp的350给我的OI生涯画上了句号。记得联赛前大概写了10遍平衡树模板,遗憾没有用上。不过代码经过联赛前反复地调整,已经少了很多需要特别注意的细节问题,基本上只要熟练就可以一遍过。如果需要参考的话,可以直接到最底端。希望各位怀揣梦想的OIer能到达理想的彼岸!
【前言】
替罪羊树是重量平衡树的一种,对于简单的平衡树应用,特别是维护的信息无法快速合并时,替罪羊树是个出色的选择。它的代码比较好理解,思想简单而暴力:对于一个节点,当左右子树的节点数量不平均时,我们就把它重构一遍。下面,我们重点阐述一下重构操作。
【基本操作】
1.拍扁重构操作:
当我们发现深度最浅的一个节点的子树不平衡时,我们从这个节点开始,对其子树进行中序遍历,同时用一个vector储存节点。代码中未提及的部分暂时忽略。
void collect(int t,vector<int>&v)
{
if(!t)return;
collect(ch[t][0],v);//遍历左子树
if(real[t])v.push_back(t);//保存当前节点
else del_place(t);
collect(ch[t][1],v);//遍历右子树
}
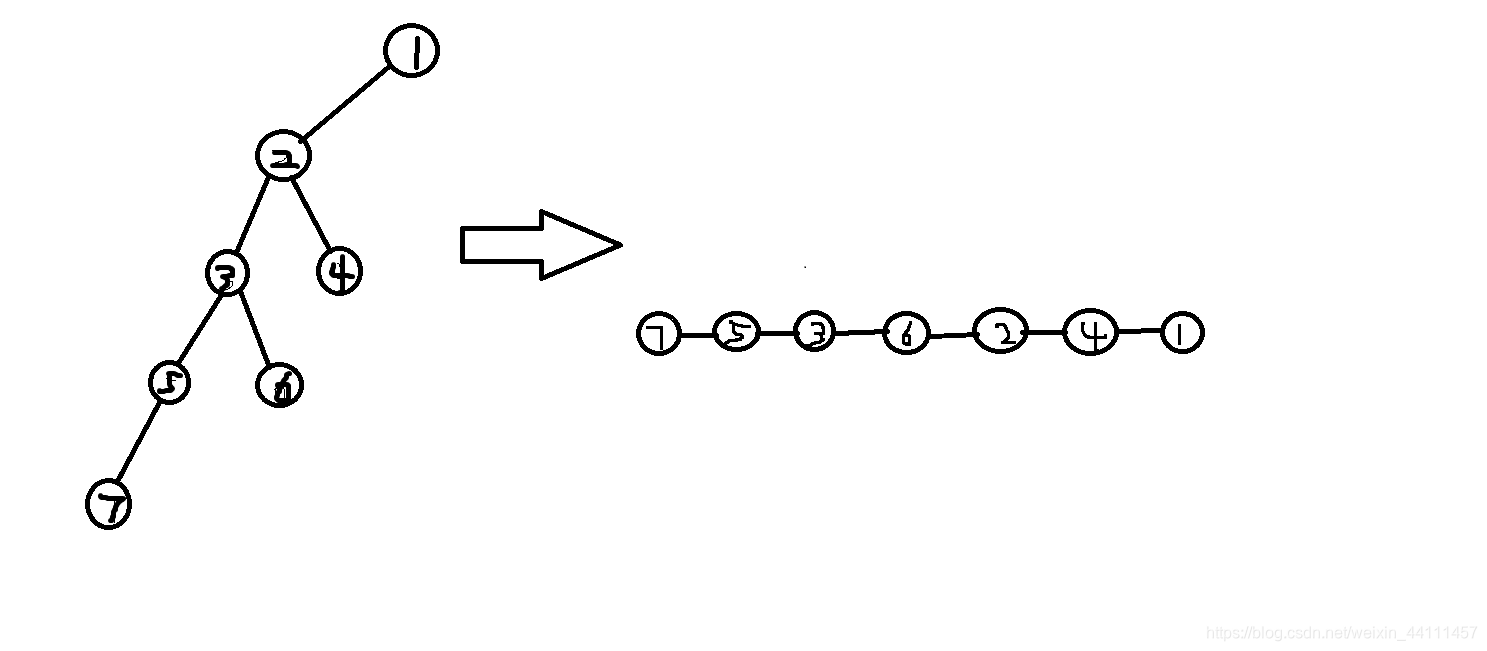
之后,我们从vector中找到最中间的节点,让它成为新的子树的根,然后递归构造它的左子树和右子树。由于是中序遍历,所以我们可以保证其二叉查找树的性质不被破坏。这样,我们得到的新的结构的树就是一个严格的完全二叉树,深度保证了严格的log。
int divide(int l,int r,vector<int> v)
//l,r是左闭右开的区间
{
if(l>=r)return 0;//当前区间为空
int mid=(l+r)>>1;
int t=v[mid];
ch[t][0]=divide(l,mid,v);
//递归构造左子树
ch[t][1]=divide(mid+1,r,v);
//递归构造右子树
fa[ch[t][0]]=fa[ch[t][1]]=t;
//确立父子关系
pushup(t);//维护子树信息
return t;//返回当前构造的子树的根
}
void rebuild(int &t)
{
static vector<int>v;
v.clear();
int f=fa[t];
collect(t,v);//中序遍历子树
t=divide(0,v.size(),v);//重构子树
fa[t]=f;
}
从代码中我们看得出的确很暴力,满满的O(n)。总结起来就是一句话:拍扁,拎起来。
2.删除操作
由于替罪羊树不是基于旋转的平衡树,它的删除操作不能通过移动节点达到目的。这里,我们用一个real数组表示当前节点是否被删除。为了更好地保证替罪羊树的时间复杂度,除了子树的size维护子树未删除的节点的个数,我们还需要用一个all数组表示当前子树所有节点个数(包括没有删除的和已经删除的节点)。如果大量删除的节点未得到清理的话,我们的时间复杂度难以得到保证,因此我们引入一个平衡因子作为阈值,当siz和all的比值大于这个阈值时,我们就重构整棵树,回收已经删除的节点,即上文collect函数的del_place函数。
void erase(int t,int k)
{
siz[t]--;
if(real[t]&&k==siz[ch[t][0]]+real[t]){real[t]=0;return;}
if(k<=siz[ch[t][0]])erase(ch[t][0],k);
else erase(ch[t][1],k-siz[ch[t][0]]-real[t]);
}
void erase(int vl)
{
erase(root,rank(vl));
if(siz[root]<alpha*all[root])rebuild(root);
//判断all和siz的比例,是否需要重构
}
3.回收空间
对于已经删除的节点,我们保存了它的儿子,父亲,siz,all等无用信息,十分浪费空间,因此我们用一个数组保存已经删除的节点,每当我们新建节点时,就优先使用已经删除的节点编号,如果没有,再执行++tot。
int st[N],top,tot;
int get_place(){return top?st[top--]:++tot;}
void del_place(int t){st[++top]=t;}
4.关于平衡树一般操作的注意
替罪羊树的一个很大的特点就是树中有一些已经删除的节点,因此我们在查找前驱后继或元素排名时一定要注意判断当前节点是否被删除。
5.插入操作
这个操作和一般的平衡树的插入操作差不多,只不过我们需要用一个变量res来保存深度最小的不合法的点,如果存在这样的点,我们就要对子树进行重构。
int insert(int &t,int vl)
{
if(!t)
{
t=newnode(vl);//新建节点
return 0;
}
siz[t]++;all[t]++;
int res;
int d= vl>val[t];//判断添加在左子树还是右子树
res=insert(ch[t][d],vl);//
pushup(t);
if(check(t))res=t;
return res;
//返回子树内深度最小的不平衡的点,没有则为0
}
void insert(int vl)
{
int t=insert(root,vl);
if(!t)return;
if(t==root)rebuild(root);
else{
int d=get(t);
rebuild(ch[fa[t]][d]);
}
}
6.平衡因子的选择
平衡因子是用于判断子树是否平衡以及all和siz的比例是否过大的一个常数。我们一般定为0.75。当然,具体情况具体分析,我们可以注意到平衡因子在略大的情况下,重构操作会变少,因此插入的时间会有所降低,但是树高也会因此变大,查找时间会增大。平衡因子在偏小的时候,重构操作会增多,因此插入时间复杂度增大,但是树高因此变小,查找操作的时间也变小。一般情况下取 0.6 到 0.7 左右的平衡因子就能满足大部分需求。对于一些各类操作数量极不均衡的题目,可以适当调整平衡因子的大小。
bool check(int t){return max(all[ch[t][0]],all[ch[t][1]])>=alpha*all[t];}
//返回1表示该子树不平衡
完整代码在最下面。
【替罪羊树应用】
一般来说,替罪羊树比较特别的应用是后缀平衡树。其实思想也非常简单,主要是需要一个技巧:
比较平衡树内两个点的中序遍历的位置先后关系。具体本人在此不再赘述,有兴趣的朋友可以参考后缀平衡树的相关国家集训队论文。这里提供一个模板:
这是一道线段树+后缀平衡树的模板题。
题面:给定一个字符串和一个序列。序列里的每一个数的大小表示这是字符串里的第几个后缀。每次询问序列里的一个区间里所有数表示的后缀中最小的一个。支持在字符串前面增加一个字符,单点修改序列的数。
思路:假设我们可以 比较两个后缀的大小关系,就可以 合并区间信息,那么我们就可以很轻松地利用线段树解决上面这个问题:单点修改,区间查询。那么怎么比较后缀呢?由于需要动态添加字符,直接用后缀平衡树就可以了,每次相当于增加一个后缀,时间复杂度 。当然,如果不会后缀平衡树,这道题还可以hash实现 合并区间信息,总时间复杂度 。
后缀平衡树代码:
#include<bits/stdc++.h>
#define re register
using namespace std;
const int N=1e6+5;
int n,m,a[N],b,c,len;
typedef long long ll;
ll ret=0;
inline int red(){
int data=0;bool w=0; char ch=getchar();
while(ch!='-' && (ch<'0' || ch>'9')) ch=getchar();
if(ch=='-') w=1,ch=getchar();
while(ch>='0' && ch<='9') data=(data<<3)+(data<<1)+ch-'0',ch=getchar();
return w?-data:data;
}
char s[N];
int las=0;
namespace tree{
int siz[N],ch[N][2],rt=0,*need;
double ll[N],rr[N],val[N];
const double alpha=0.75;
inline bool cmp(const int a,const int b){
if(s[a]!=s[b])return s[a]<s[b];
return val[a-1]<val[b-1];
}
inline bool check(const int&u){return max(siz[ch[u][0]],siz[ch[u][1]])>=siz[u]*alpha;}
void collect(int u,vector<int>&v){
if(ch[u][0])collect(ch[u][0],v);
v.push_back(u);
if(ch[u][1])collect(ch[u][1],v);
}
int build(int l,int r,vector<int>&v,double ls,double rs){
if(l>=r)return 0;
int mid=(l+r)>>1;
int u=v[mid];siz[u]=r-l;
val[u]=ls+rs;ll[u]=ls;rr[u]=rs;
ch[u][0]=build(l,mid,v,ls,val[u]/2);
ch[u][1]=build(mid+1,r,v,val[u]/2,rs);
return u;
}
inline void rebuild(int&u){
static vector<int>v;v.clear();
collect(u,v);u=build(0,v.size(),v,ll[u],rr[u]);
}
void insert(int &u,const int&v,const double l,const double r){
if(!u)return (void)(u=v,ll[u]=l,rr[u]=r,siz[u]=1,val[u]=l+r);
++siz[u];double mid=(l+r)/2;
if(cmp(v,u))insert(ch[u][0],v,l,mid);
else insert(ch[u][1],v,mid,r);
if(check(u))need=&u;
}void ins(const int&v){
need=NULL;insert(rt,v,-1e9,1e9);
if(need!=NULL)rebuild(*need);
}
}
using tree::val;
namespace sgt{
#define lc (p<<1)
#define rc (p<<1|1)
int mx[N<<1|1];
inline bool cmp(const int&x,const int&y){return a[x]==a[y]?x<y:val[a[x]]<val[a[y]];}
inline void pushup(const int&p){mx[p]=cmp(mx[lc],mx[rc])?mx[lc]:mx[rc];}
void build(const int p,const int l,const int r){
if(l==r)return mx[p]=l,void();
int mid=(l+r)>>1;
build(lc,l,mid);build(rc,mid+1,r);
pushup(p);
}
void change(int p,int l,int r,int pos){
if(l==r)return;int mid=(l+r)>>1;
if(pos<=mid)change(lc,l,mid,pos);
else change(rc,mid+1,r,pos);
pushup(p);
}
int query(int p,int l,int r,int ql,int qr){
if(ql<=l&&qr>=r)return mx[p];
int mid=(l+r)>>1;
if(qr<=mid)return query(lc,l,mid,ql,qr);
if(ql>mid)return query(rc,mid+1,r,ql,qr);
int p1=query(lc,l,mid,ql,qr),p2=query(rc,mid+1,r,ql,qr);
return cmp(p1,p2)?p1:p2;
}
}
int main(){
n=red();m=red();len=red();
scanf("%s",s+1);reverse(s+1,s+len+1);
for(int re i=1;i<=len;i++)tree::ins(i);
for(int re i=1;i<=n;i++)a[i]=red();
sgt::build(1,1,n);
while(m--){
char op=getchar();
while(op!='I'&&op!='Q'&&op!='C')op=getchar();
if(op=='I'){
s[++len]=(red()^las)+'a';
tree::ins(len);
}if(op=='C'){
int pos=red();a[pos]=red();
sgt::change(1,1,n,pos);
}if(op=='Q'){
int l=red(),r=red();
cout<<(las=sgt::query(1,1,n,l,r))<<"\n";
}
}
}
【小结】
替罪羊树虽然不基于旋转机制,但是其思路非常清晰,代码量非常的小,在速度上也不慢,无论是时间复杂度,实现复杂度和思维复杂度都不输给传统平衡树。但是替罪羊树由于其平衡机制的限制,并不能支持一些复杂的操作,比如常用Splay 来处理的提取区间的操作。同时由于它是一个用势能来分析的均摊结构,也无法简单的进行可持久化。对于简单的平衡树应用,特别是维护的信息无法快速合并时,替罪羊树是个出色的选择。
例题:【普通平衡树】
完整代码:
#include<cstdio>
#include<iostream>
#include<queue>
#include<algorithm>
#include<cstring>
#include<string>
#include<vector>
#include<cmath>
#define re register
#define LL long long
using namespace std;
int n,m,a,b,c;
inline int red()
{
int data=0;int w=1; char ch=0;
ch=getchar();
while(ch!='-' && (ch<'0' || ch>'9')) ch=getchar();
if(ch=='-') w=-1,ch=getchar();
while(ch>='0' && ch<='9') data=(data<<3)+(data<<1)+ch-'0',ch=getchar();
return data*w;
}
struct node{
static const int N=2e5+5;
static const double alpha=0.75;
int st[N],top,tot;
int get_place(){return top?st[top--]:++tot;}
void del_place(int t){st[++top]=t;}
void clean_st(){top=tot=0;}
int root;
int ch[N][2],fa[N];
int val[N],siz[N],all[N];
bool real[N];
void pushup(int p){
all[p]=all[ch[p][0]]+all[ch[p][1]]+1;
siz[p]=siz[ch[p][0]]+siz[ch[p][1]]+real[p];
}
bool check(int t){return max(all[ch[t][0]],all[ch[t][1]])>=alpha*all[t];}
int newnode(int w=0,int f=0){
int t=get_place();
ch[t][1]=ch[t][0]=0;
val[t]=w;
siz[t]=all[t]=1;
real[t]=1;
fa[t]=f;
return t;
}
void collect(int t,vector<int>&v)
{
if(!t)return;
collect(ch[t][0],v);
if(real[t])v.push_back(t);
else del_place(t);
collect(ch[t][1],v);
}
int divide(int l,int r,vector<int> v)
{
if(l>=r)return 0;
int mid=(l+r)>>1;
int t=v[mid];
ch[t][0]=divide(l,mid,v);
ch[t][1]=divide(mid+1,r,v);
fa[ch[t][0]]=fa[ch[t][1]]=t;
pushup(t);
return t;
}
void rebuild(int &t)
{
static vector<int>v;
v.clear();
int f=fa[t];
collect(t,v);
t=divide(0,v.size(),v);
fa[t]=f;
}
int rank(int vl)
{
int t=root,ans=1;
while(t)
{
if(vl<=val[t])t=ch[t][0];
else
{
ans+=siz[ch[t][0]]+real[t];
t=ch[t][1];
}
}
return ans;
}
int get_kth(int k)
{
int t=root;
while(t)
{
if(siz[ch[t][0]]+1==k&&real[t])return val[t];
if(siz[ch[t][0]]>=k)t=ch[t][0];
else{
k-=siz[ch[t][0]]+real[t];
t=ch[t][1];
}
}
}
int get(int u){return u==ch[fa[u]][1];}
int insert(int &t,int vl)
{
if(!t)
{
t=newnode(vl);
return 0;
}
siz[t]++;all[t]++;
int res;
int d= vl>val[t];
res=insert(ch[t][d],vl);
pushup(t);
if(check(t))res=t;
return res;
}
void insert(int vl)
{
int t=insert(root,vl);
if(!t)return;
if(t==root)rebuild(root);
else{
int d=get(t);
rebuild(ch[fa[t]][d]);
}
}
void erase(int t,int k)
{
siz[t]--;
if(real[t]&&k==siz[ch[t][0]]+real[t]){real[t]=0;return;}
if(k<=siz[ch[t][0]])erase(ch[t][0],k);
else erase(ch[t][1],k-siz[ch[t][0]]-real[t]);
}
void erase(int vl)
{
erase(root,rank(vl));
if(siz[root]<alpha*all[root])rebuild(root);
}
int pre(int vl){
return get_kth(rank(vl)-1);
}
int nxt(int vl){
return get_kth(rank(vl+1));
}
}sgt;
int main()
{
scanf("%d",&n);
while(n--)
{
int opt,t;
opt=red();t=red();
switch(opt)
{
case 1:sgt.insert(t);break;
case 2:sgt.erase(t);break;
case 3:printf("%d\n",sgt.rank(t));break;
case 4:printf("%d\n",sgt.get_kth(t));break;
case 5:printf("%d\n",sgt.pre(t));break;
case 6:printf("%d\n",sgt.nxt(t));break;
}
}
}
更简单的代码实现:
#include<bits/stdc++.h>
#define re register
using namespace std;
int n,m;
const int N=1e5+5;
inline int red(){
int re data=0;bool re w=0;char re ch=getchar();
while((ch<'0'||ch>'9')&&ch!='-')ch=getchar();
if(ch=='-')w=1,ch=getchar();
while(ch>='0'&&ch<='9')data=data*10+ch-48,ch=getchar();
return w?-data:data;
}
int st[N],tot=0,top=0,rt=0,*need;
int ch[N][2],val[N],all[N],siz[N];
bool rel[N];//表示该点是否删除
const double alpha=0.75;
inline int node(int v){//新建权值为v的点,返回点的编号
int u=top?st[top--]:++tot;
val[u]=v;siz[u]=all[u]=rel[u]=1;
ch[u][0]=0;ch[u][1]=0;//这一步很重要,写的时候别忘了
return u;
}
void insert(int&u,int v){
if(!u)return u=node(v),void();
++siz[u],++all[u];
if(v<=val[u])insert(ch[u][0],v);
else insert(ch[u][1],v);
if(max(all[ch[u][0]],all[ch[u][1]])>=all[u]*alpha)need=&u;
//注意need直接指向父亲的儿子信息的地址,修改need就直接修改了父亲的儿子的信息
}
vector<int>v;
void dfs(int u){
if(ch[u][0])dfs(ch[u][0]);
if(rel[u])v.push_back(val[u]);st[++top]=u;//回收空间
if(ch[u][1])dfs(ch[u][1]);
}
int build(int l,int r){
if(l>=r)return 0;//这里的区间是左闭右开的
int mid=(l+r)>>1,u=node(v[mid]);
ch[u][0]=build(l,mid);
ch[u][1]=build(mid+1,r);
all[u]=all[ch[u][0]]+all[ch[u][1]]+1;
siz[u]=siz[ch[u][0]]+siz[ch[u][1]]+rel[u];
return u;
}
void rebuild(int &u){
v.clear();dfs(u);
u=build(0,v.size());//这一步操作就会更新原父亲的儿子信息
}
void insert(int v){
need=NULL;insert(rt,v);
if(need!=NULL)rebuild(*need);
}
int rank(int u,int v){//以下均为递归实现
if(!u)return 1;
return v<=val[u]?rank(ch[u][0],v):rank(ch[u][1],v)+siz[ch[u][0]]+rel[u];
}
int kth(int u,int k){
if(rel[u]&&k==siz[ch[u][0]]+1)return val[u];
if(siz[ch[u][0]]>=k)return kth(ch[u][0],k);
else return kth(ch[u][1],k-siz[ch[u][0]]-rel[u]);
}
void erase(int u,int k){//这一步可以直接复制kth函数再略作修改
--siz[u];
if(rel[u]&&k==siz[ch[u][0]]+1)return rel[u]=0,void();
if(siz[ch[u][0]]>=k)erase(ch[u][0],k);
else erase(ch[u][1],k-siz[ch[u][0]]-rel[u]);
}
void erase(int v){
erase(rt,rank(rt,v));
if(all[rt]*alpha>=siz[rt])rebuild(rt);
}
void print(int x){//这里没有判断负数,要用的话自己改一下吧
if(x>9)print(x/10);
putchar(x%10^48);
}
int main(){
n=red();
while(n--){
int op=red(),t=red();
switch(op){
case 1:insert(t);break;
case 2:erase(t);break;
case 3:print(rank(rt,t));break;
case 4:print(kth(rt,t));break;
case 5:print(kth(rt,rank(rt,t)-1));break;
case 6:print(kth(rt,rank(rt,t+1)));break;
}if(op>2)putchar('\n');
}
}
