理解主成分分析

译者注：

• 本文翻译自 Rishav Kumar 于 2019 年 1 月 2 日发表的文章 Understanding Principal Component Analysis
• 文中括号或者引用块中的 斜体字 为对应的英文原文或者我自己注释的话（会标明「译者注」），否则为原文中本来就有的话
• 文中的「我」均指原作者 Rishav Kumar
• 目录保留英文原文
• 本人水平有限，如有错误欢迎指出
• 能力尚可建议阅读英文原文
• 文章同步发表至 我的个人独立博客

本文的目的是让读者能够通过必要的数学证明来详细了解主成分分析。

在现实世界的数据分析任务中，我们面对的数据通常较为复杂，例如多维数据。我们绘制数据并希望从中找到各种模式，或者使用数据来训练机器学习模型。一种看待维度（dimensions）的方法是假设你有一个数据点 $x$，如果我们把这个数据点想象成一个物理对象，那么维度就是仅仅是一个视图（译者注：这里的视图应该是和三视图中的视图是一个概念）的基础（basis of view），就像从横轴或者纵轴观察数据时的位置。

随着数据维度的增长，可视化数据的难度和数据计算量也随之增长。所以，如何减少数据维度？

• 较少冗余的维度
• 仅仅保留最重要的维度

break1

首先来理解一些术语：

方差（Variance）：它是数据离散程度的一个度量方法。数学上来说，就是数据与其平均值的误差平方和的平均。我们使用如下的公式来计算方差 $var(x)$：

$var(x) = \frac{\Sigma(x_i-\bar{x})^2}{N}$

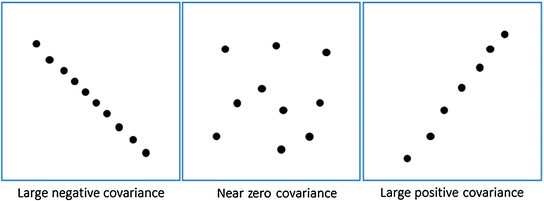
协方差（Covariance）：它衡量两组有序数据中相应元素在同一方向上移动的程度（译者注：或者通俗的来讲，就是表示两个变量的变化趋势）。两个变量 $x$ 和 $y$ 的协方差 $cov(x,y)$ 可以如下计算：

$cov(x,y) = \frac{\Sigma(x_i-\bar{x})(y_i-\bar{y})}{N}$

其中， $x_i$ 是 $x$ 在第 $i$ 个维度的值（译者注：注意和 Python 中的多维列表中的「维」做区分，数学上来说，这里的 $x$ 只是一个向量）， $\bar{x}$ 和 $\bar{y}$ 是相应的平均值。

协方差的一种理解方式是两个数据集是如何相关关联的。

正协方差意味着 $X$ 和 $Y$ 是正相关的，即 $X$ 增长 $Y$ 也增长。负协方差则意味着完全相反的关系。然而协方差为零意味着 $X$ 和 $Y$ 不相关。

Continue break1

现在让我们来考虑一下数据分析的需求。

由于我们想要找到数据中的模式，所以我们希望数据分布在每个维度上。同时，我们也希望各个维度之间是独立的。这样的话如果数据在某些 $n$ 维表示中具有高协方差时，我们可以用这些 $n$ 维的线性组合来替代原来的维度。现在数据就变成仅仅依赖于这 $n$ 维的线性组合了。

那么，主成分分析（PCA）是干什么的？

PCA 试图寻找一组新的维度（或者叫一组基础视图），使得所有维度都是正交的（所以线性无关），并根据数据在他们上面的方差进行排序。这就意味着越重要的成分越会排在前面（越重要 = 更大方差/数据分布更广）

PCA 的步骤如下：

1. 计算数据点的协方差矩阵 $X$
2. 计算特征向量和相应的特征值
3. 根据特征值，降序排列对应的特征向量
4. 选择前 $k$ 个特征向量作为新的 $k$ 维
5. 将原始的 $n$ 维数据变换为 $k$ 维

为了理解 PCA 的详细计算过程，你需要对特征向量（eigen vectors）和特征值（eigen values）有所了解，你可以参考这个对特征值和特征向量的直观解释。

确保在继续阅读之前你已经理解了特征向量和特征值。

$[Covariance matrix] \cdot [Eigenvector] = [eigenvalue] \cdot [Eigenvector]$

假设我们已经了解了方差和协方差，然后我们来看下协方差矩阵是什么样的：

$\begin{bmatrix} V_a & C_{a,b} & C_{a,c} & C_{a,d} & C_{a,e} \\ C_{a,b} & V_b & C_{b,c} & C_{b,d} & C_{b,e} \\ C_{a,c} & C_{b,c} & V_c & C_{c,d} & C_{c,e} \\ C_{a,d} & C_{b,d} & C_{c,d} & V_d & C_{d,e} \\ C_{a,e} & C_{b,e} & C_{c,e} & C_{d,e} & V_e \\ \end{bmatrix}$

上面的矩阵即是一个 5 维数据集的协方差矩阵（译者注：原文说是 4 维，我觉得有可能笔误，我这里更正为 5 维），a、b、c、d 和 e。其中 $V_a$ 表示在 a 维度上的方差， $C_{a,b}$ 表示 a 与 b 之间的协方差。

如果我们有一个 $m \times n$ 的矩阵，也就是说有 $n$ 个数据点，每个数据点 $m$ 维（译者注：这是原文的说法，暂且将数据点理解为样本，我个人觉得，一般是以行表示样本，列表示特征，而这里的说法正好相反），然后协方差矩阵可以如下计算：

$C_x = \frac{1}{n-1}(X-\bar{X})(X-\bar{X})^T$

其中 $X^T$ 是 $X$ 的转置。

需要注意的是，协方差矩阵包括：

• 每个维度上的方差作为主对角线元素
• 每两个维度之间的协方差作为非对角线元素

而且，协方差矩阵是对称的。正如我们之前说的那样，我们希望数据分布的更广，即它应该在某个维度上具有高方差。我们也想要去除相关性高的维度，即维度之间的协方差应该为 0（他们应该是线性无关的）。因此，我们的协方差矩阵应该具有：

• 主对角线元素的值比较大
• 非对角线元素为 0

我们称之为对角阵（diagonal matrix）。

所以我们必须变换原始数据点，才能使得他们的协方差矩阵为对角阵。把一个矩阵变换为对角阵的过程称为对角化（diagonalization）。

在进行 PCA 之前记得归一化（normalize）你的数据，因为如果我们使用不同尺度的数据（即这里的特征），我们会得到误导性的成分。如果特征尺度不同，那么我们也可以简单地使用相关性矩阵而不是协方差矩阵。为了简化这篇文章，我假设我们已经归一化了数据。

让我们来定义一下 PCA 的目标：

• 找到可以无损地表示原始数据的线性无关的维度（或者基础视图）
• 这些新找到的维度应该能够让我们预测或者重建原始维度，同时应该最小化重建或者投影误差

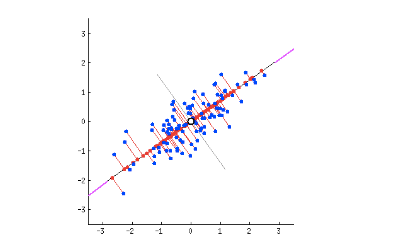
让我们来理解一下我所说的投影误差。假设我们要把一个 2 维数据变换成 1 维。所以我们就需要找到一条直线然后把数据点投影到上面（一条直线就是 1 维的）。我们可以找到很多条直线，让我们来看下其中两种：

假设洋红色（magenta）线就是我们的新维度。

如果你看到了红色线（连接蓝色点的投影和洋红色线），那么这每个数据点到直线的垂直距离就是投影误差。所有数据点的误差的和就是总投影误差（译者注：这里每个数据点的误差可以是绝对值形式或者平方误差形式）。

我们的新数据点就是原始蓝色数据点的投影（红点）。正如我们所看到的，我们将 2 维数据投影到 1 维空间，从而将他们变换成 1 维数据。那条洋红色的线被称为主轴（principal axis）。由于我们是投影到一个维度，所有我们只有一个主轴。

很明显，我们选择的第二条直线就比较好，因为

• 投影误差比第一条直线小
• 与第一种情况相比，投影后的数据点分布更广，即方差更大

上面提到的两点是有联系的，即如果我们最小化重建误差，那么方差也会增大。

为什么？

证明：https://stats.stackexchange.com/questions/32174/pca-objective-function-what-is-the-connection-between-maximizing-variance-and-m/136072#136072

到现在为止我们做的有：

• 我们已经计算了原始数据矩阵 $X$ 的协方差矩阵

现在我们要变换原始数据点，使得变换后的数据协方差矩阵为对角阵。那么如何做呢？

$Y=PX$

其中， $X$ 为原始数据集， $Y$ 为变换后的数据集。

为了简便，我们忽略平均项并且假设数据已经中心化（be centered），即 $X = (X - \bar{X})$，那么

$\begin{aligned} C_x &= \frac{1}{n}XX^T \\ C_y &= \frac{1}{n}YY^T \\ &= \frac{1}{n}(PX)(PX)^T \\ &= \frac{1}{n}PXX^TP^T \\ &= P(\frac{1}{n}XX^T)P^T \\ &= PC_xP^T \end{aligned}$

这就是其中的原理：如果我们能找到 $C_x$ 的特征向量矩阵并且用其作为矩阵 $P$（ $P$ 用于将 $X$ 变换为 $Y$，看上面的公式），那么 $C_y$（变换后数据的协方差） 就是对角阵。所以 $Y$ 就是新的变换后的数据点。

现在，如果我们想要将数据变换为 $k$ 维，那么我们可以选择矩阵 $C_x$ 的前 $k$ 个特征向量（根据特征值降序排列）组成一个矩阵，这就是矩阵 $P$。

如果我们有 $m$ 维的 $n$ 个原始数据点，那么

$X:m \times n$

$P:k \times m$

$Y=PX:(k \times m)(m \times n)=(k \times n)$

所以，我们变换后的矩阵将是 $n$ 个数据点 $k$ 维。

但是为什么这个原理有效呢？

证明：

首先让我们来看一些定理：

• 定理 1：正交矩阵的逆是其转置，为什么？

  令 $A$ 是一个 $m \times n$ 的正交矩阵（译者注：根据定义，正交矩阵一定是方阵，此处应 $m=n$）， $a_i$ 是第 $i$ 个列向量，矩阵 $A^TA$ 的第 $ij$ 个元素为：

  $\begin{aligned} (A^TA)_{ij} &= a_i^Ta_j \\\\ &= \begin{cases} 1, & \text{if $i$ = $j$} \\\\ 0, & \text{otherwise} \end{cases} \end{aligned}$

  即 $A^TA = I$，所以 $A^{-1} = A^T$

• 定理 2：

  令 $A$ 是一个实对称矩阵， $\lambda_1,\lambda_2,\cdots,\lambda_k$ 是 $A$ 的不同的特征值， $u_i \in R^n$ 非零，且 $1 \leq i \leq k$，那么 ${u_1,u_2,\cdots,u_k}$ 就组成一个正交规范集（orthonormal set）。

  证明：

  对于 $i \neq j$，且 $1 \leq i,j \leq k$，由于 $A^T = A$，我们有

  $\begin{aligned} \lambda_i \langle u_i,u_j \rangle &= \langle \lambda_iu_i,u_j \rangle \\\\ &= \langle Au_i,u_j \rangle \\\\ &= \langle u_i,A^Tu_j \rangle \\\\ &= \langle u_i,Au_j \rangle \\\\ &= \lambda_j \langle u_i,u_j \rangle \\\\ \end{aligned}$

  由于 $i \neq j$，我们有 $\lambda_i \neq \lambda_j$，所以 $\langle u_i, u_j \rangle = 0$。

• 定理 3：

  令 $A$ 为 $n \times n$ 的实对称矩阵且所有特征值都不相同，那么存在一个正交矩阵 $P$，使得 $P^{-1}AP=D$，其中 $D$ 为对角阵，对角元素为 $A$ 的特征值。

  证明：

  令 $A$ 有特征值 $\lambda_1,\lambda_2,\cdots,\lambda_n$， $u_i \in R^n$ 且 $|u_i| = 1$， $Au_i=\lambda_iu_i$， $1 \leq i \leq n$。通过推论，矩阵 $P=[u_1,u_2,\cdots,u_n]$ 是可逆的且 $P^{-1}AP=D$，是一个对角阵。而且，由定理 2， $(u_1,u_2,\cdots,u_n)$ 是一个正交规范集，所以 $P$ 确实是一个正交矩阵。

有了这些定理，我们可以说：

一个对称阵可以通过其正交特征向量进行对角化。正交规范向量（orthonormal vectors）只是规范化的正交向量（orthogonal
vectors）。

译者注：关于 orthonormal vectors 和 orthogonal
vectors 的区别可参见 6.3 Orthogonal and orthonormal vectors - UCL，我摘抄部分如下：

Definition. We say that 2 vectors are orthogonal if they are perpendicular to each other. i.e. the dot product of the two vectors is zero.

Definition. A set of vectors S is orthonormal if every vector in S has magnitude 1 and the set of vectors are mutually orthogonal.

$\begin{aligned} C_y &= PC_xP^T \\\\ &= P(E^DE)P^T \\\\ &= P(P^TDP)P^T \\\\ &= (PP^T)D(PP^T) \\\\ &= (PP^{-1})D(PP^{-1}) \\\\ C_Y &= D \end{aligned}$

很明显是 $P$ 对角化了 $C_y$。这就是 PCA 的目标，我们可以使用矩阵 $P$ 和 $C_y$ 来总结 PCA 的结果。

• X 的主成分是 $C_x$ 的特征向量
• $C_y$ 的第 $i$ 个对角元素是 $X$ 在 $i$ 维度上的方差

总结：

$[\text{new data}]_{k\times n} = [\text{top $k$ eigenvectors}]_{k \times m}[\text{original data}]_{m \times n}$

Note：PCA 是一种分析方法。你可以使用 SVD 做 PCA，或者使用特征分解（就像我们这里做的一样）做 PCA，或者使用其他方法做 PCA。SVD 只是另一种数值方法。所以不要混淆 PCA 和 SVD 这两个术语。但是有时我们会因为性能因素选择 SVD 而不是特征分解或者其他方法（这个不用关心），我们会在接下来的文章中探索 SVD。

译者注：关于 SVD，有兴趣的话可以参考我写的另一篇文章：奇异值分解 SVD 的数学解释。