K-均值(K-means算法)算法学习笔记
——慕课-商务数据分析(复旦大学 -赵卫东/董亮) 学习笔记
文章目录
一.聚类分析简介
聚类分析是一种典型的无监督学习,用于对未知类别的样本进行划分,将它们按照一定的规则划分成若干个类族,把相似(距高相近)的样本聚在同一个类簇中,把不相似的样本分为不同的类簇,从而揭示样本之间内在的性质以及相互之间的联系规律。
聚类算法在银行,零售,保险,医学,军事等诸多领域有着广泛的应用。
二.基于划分的聚类方法
基于划分的方法是简单、常用的一种聚类方法。通过将对象划分为互斥的簇进行聚类,每个对象仅属于一个簇。划分结果旨在使簇之间的相似性低,簇内的相似度高,基于划分的常用算法有K均值(K-means算法)、k-medoids、k-prototype等。
三.K-均值(K-means)算法简介
K-均值(K-means)聚类是基于划分的聚类算法,是一种迭代算法。计算样本点与类簇质心的距离,与类簇质心相近的样本点划分为同一类簇。K-均值通过样本点间的距离来衡量他们之间的相似度,两个样本距离越远,则相似度越低,否则相速度越高。K-均值(K-means)算法不适用于非凸面形状(非球形)的数据集,例如图中的例子,聚类结果与初始目标有非常大的差别。

K-均值算法聚类步骤如下:
1.首先选取K个类簇(K需要用户进行指定)的质心,通常是随机选取。
2.对剩余的每个样本点,计算它们到各个质心的欧式距离,并将其归入到相互间距离最小的质心所在的簇。计算各个新簇的质心。
3.在所有样本点都划分完毕后,根据划分情况重新计算各个簇的质心所在的位置,然后迭代计算各个样本点到各簇质心的距离,对所有样本点进行重新划分。
4.重复第2和第3步,直到迭代计算后,所有样本点的划分情况保持不变,此时说明k-均值算法已经得到了最优解,将运行结果返回。
四.K-均值(K-means)算法过程
K-means工作流程:
K-means算法计算步骤基本上可以概括为两个部分:
1.计算每一个对象到类簇中心的距离;
2.根据类簇内的对象计算新的簇类中心。
创建k个点作为起始质心(多是随机选择)
repeat
对数据集中的每个数据点
repeat
对每个质心
计算质心与数据点之间的距离
将数据点分配到距离其最近的类(或簇)
对每一个类(簇),计算类(簇)中所有点的均值并将其作为质心。
K-means开发流程:
收集数据:使用任意方法
准备数据:需要数值型数据类计算距离, 也可以将标称型数据映射为二值型数据再用于距离计算。
分析数据:使用任意方法
训练算法:无监督学习不需要训练步骤
测试算法:应用聚类算法、观察结果.可以使用量化的误差指标如误差平方和(后面会介绍)来评价算法的结果.
使用算法:可以用于所希望的任何应用.通常情况下, 簇质心可以代表整个簇的数据来做出决策.
五.K值的选取
1.与层次类聚算法结合,先通过层次类聚算法得出大致的类聚数目,并且获得一个初始聚类结果,然后再通过K-均值法改进聚类结果。
2.基于系统演化的方法,将数据集视为伪热力学系统,在分裂和合并的过程中,将系统演化到稳定平衡状态而确定K值。
另外在网络上看到了手肘法和轮廓系数法
https://blog.csdn.net/qq_15738501/article/details/79036255
六.K-均值(K-means)具体实现
慕课上使用python语言实现的我这里使用c++
这里用C++代码完成iris数据测试:
测试数据:iris测试数据
#include <iostream>
#include <sstream>
#include <fstream>
#include <vector>
#include <math.h>
#include <stdlib.h>
#include <time.h>
using namespace std;
#define K 3 //簇的数目
#define DIM_NUM 5
#define DATA_NUM 140
//存放元组的属性信息
typedef vector<double> Tuple;//存储一条数据记录
//输入两个元组,计算两个元组间的欧几里距离
double getDistXY(const Tuple& t1, const Tuple& t2)
{
double sum = 0;
for (int i = 1; i <= DIM_NUM; ++i)
{
sum += (t1[i] - t2[i]) * (t1[i] - t2[i]);
}
return sqrt(sum);
}
//输入k个质心和1个元组,根据质心,决定当前元组属于哪个簇
int clusterOfTuple(const Tuple means[], const Tuple& tuple){
double dist = getDistXY(means[0], tuple);
double tmp;
int label = 0; //标示属于哪一个簇
for (int i = 1; i<K; i++) //遍历质心
{
tmp = getDistXY(means[i], tuple);
if (tmp<dist) //选择距离最小的质心,用label标示
{
dist = tmp;
label = i;
}
}
return label;
}
//输入簇集和质心,获得给定簇集的平方误差
double getVar(vector<Tuple> clusters[], Tuple means[])
{
double var = 0;
for (int i = 0; i < K; i++) //遍历质心
{
vector<Tuple> t = clusters[i];
for (unsigned int j = 0; j< t.size(); j++)
{
var += getDistXY(t[j], means[i]); //簇集中所有元组到质心的距离之和
}
}
//cout<<"sum:"<<sum<<endl;
return var;
}
//输入簇,获得当前簇的均值(质心)
Tuple getMeans(const vector<Tuple>& cluster)
{
int num = cluster.size();
Tuple t(DIM_NUM + 1, 0); //初始化dimNum + 1个0填充数组
//第一个位置存放记录编号,第2到dimNum+1个位置存放实际元素
for (int i = 0; i < num; i++)
{
for (int j = 1; j <= DIM_NUM; ++j)
{
t[j] += cluster[i][j];
}
}
for (int j = 1; j <= DIM_NUM; ++j)
{
t[j] /= num;
}
return t; //返回簇集中所有元组平均值作为质心
//cout<<"sum:"<<sum<<endl;
}
void print_Means(const vector<Tuple> clusters[])
{
for (int lable = 0; lable < K; lable++)
{
cout << clusters[lable].size() << " " ;
Tuple temp = getMeans(clusters[lable]);
cout << "(";
for (int j = 0; j <= DIM_NUM; ++j)
{
cout << temp[j] << "\t";
}
cout << ")\n";
}
}
void print(const vector<Tuple> clusters[])
{
for (int lable = 0; lable<K; lable++)
{
cout << "第" << lable + 1 << "个簇:" << endl;
vector<Tuple> t = clusters[lable];
for (unsigned int i = 0; i<t.size(); i++)
{
cout << i + 1 << ".(";
for (int j = 0; j <= DIM_NUM; ++j)
{
cout << t[i][j] << ", ";
}
cout << ")\n";
}
}
}
vector<Tuple>* KMeans(vector<Tuple>& tuples)
{
vector<Tuple> clusters[K]; //k个簇
Tuple means[K]; //k个质心
int i = 0;
//一开始随机选取k条记录的值作为k个簇的质心(均值)
srand((unsigned int)time(NULL)); //随机数发生器的初始化
for (i = 0; i<K;)
{
int iToSelect = rand() % tuples.size();
if (means[iToSelect].size() == 0)
{
for (int j = 0; j <= DIM_NUM; ++j)
{
means[i].push_back(tuples[iToSelect][j]); //初始化个质心
}
++i;
}
}
int lable = 0;
//根据默认的质心,将输入的tuples分配给各个簇
for (i = 0; i != tuples.size(); ++i)
{
lable = clusterOfTuple(means, tuples[i]);
clusters[lable].push_back(tuples[i]); //初始化各簇
}
double oldVar = -1;
double newVar = getVar(clusters, means); //初始化误差和
cout << "初始的的整体误差平方和为:" << newVar << endl;
int t = 0;
//当新旧函数值相差不到1即准则函数值不发生明显变化时,算法终止
while (abs(newVar - oldVar) >= 0.01)
{
cout << "第 " << ++t << " 次迭代开始:" << endl;
for (i = 0; i < K; i++) //更新每个簇的质心
{
means[i] = getMeans(clusters[i]);
}
for (i = 0; i < K; i++) //清空每个簇
{
clusters[i].clear();
}
for (i = 0; i != tuples.size(); ++i) //根据新的质心更新簇集
{
lable = clusterOfTuple(means, tuples[i]);
clusters[lable].push_back(tuples[i]);
}
//更新误差判断值
oldVar = newVar;
newVar = getVar(clusters, means);
cout << "此次迭代之后的整体误差平方和为:" << newVar << endl;
}
cout << "The result is:\n";
print(clusters);
print_Means(clusters);
return clusters;
}
int main()
{
char fname[256] = "iris_train.txt";
ifstream infile(fname);
if (!infile){
cout << "不能打开输入的文件" << fname << endl;
return 0;
}
vector<Tuple> tuples;
//从文件流中读入数据
for (int i = 0; i<DATA_NUM && !infile.eof(); ++i)
{
string str;
getline(infile, str);
istringstream istr(str);
Tuple tuple(DIM_NUM + 1, 0);//第一个位置存放记录编号,第2到dimNum+1个位置存放实际元素
tuple[0] = i + 1;
for (int j = 1; j <= DIM_NUM; ++j)
{
istr >> tuple[j];
}
tuples.push_back(tuple);
}
cout << endl << "开始聚类" << endl;
KMeans(tuples);
system("pause");
return 0;
}
运行截图:


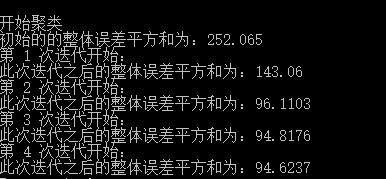
结论:
可以多运行几次以上代码,可以看出由于初始点事随机选取的每次运行得到的结果有所差异。这也是基本K-means算法的一个缺点,随着众多改进算法的提出K-means算法的这一问题也得到改善,深入了解的朋友可以查阅相关论文。
想要测试数据的朋友也可以私我。
七.K-均值(K-means)算法的优缺点
优点:
1.聚类效果较优。
2.原理简单,实现容易,收敛速度快。
3.需要调整的参数较少,通常只需要调整簇数K。
缺点:
1.在 K-means 算法中 k 需要事先确定,这个 k 值的选定有时候是比较难确定。
2.在 K-means 算法中,首先需要初始k个聚类中心,然后以此来确定一个初始划分,然后对初始划分进行优化。这个初始聚类中心的选择对聚类结果有较大的影响,一旦初始值选择的不好,可能无法得到有效的聚类结果。多设置一些不同的初值,对比最后的运算结果,一直到结果趋于稳定结束。
3.该算法需要不断地进行样本分类调整,不断地计算调整后的新的聚类中心,因此当数据量非常大时,算法的时间开销是非常大的。
4.对离群点很敏感。
5.从数据表示角度来说,在 K-means 中,我们用单个点来对 cluster 进行建模,这实际上是一种最简化的数据建模形式。这种用点来对 cluster 进行建模实际上就已经假设了各 cluster的数据是呈圆形(或者高维球形)或者方形等分布的。不能发现非凸形状的簇。但在实际生活中,很少能有这种情况。所以在 GMM 中,使用了一种更加一般的数据表示,也就是高斯分布。
6.从数据先验的角度来说,在 K-means 中,我们假设各个 cluster 的先验概率是一样的,但是各个 cluster 的数据量可能是不均匀的。举个例子,cluster A 中包含了10000个样本,cluster B 中只包含了100个。那么对于一个新的样本,在不考虑其与A cluster、 B cluster 相似度的情况,其属于 cluster A 的概率肯定是要大于 cluster B的。
7.在 K-means 中,通常采用欧氏距离来衡量样本与各个 cluster 的相似度。这种距离实际上假设了数据的各个维度对于相似度的衡量作用是一样的。但在 GMM 中,相似度的衡量使用的是后验概率 αcG(x|μc,∑c)αcG(x|μc,∑c) ,通过引入协方差矩阵,我们就可以对各维度数据的不同重要性进行建模。
8.在 K-means 中,各个样本点只属于与其相似度最高的那个 cluster ,这实际上是一种 hard clustering 。
针对K-means算法的缺点,很多前辈提出了一些改进的算法。例如 K-modes 算法,实现对离散数据的快速聚类,保留了K-means算法的效率同时将K-means的应用范围扩大到离散数据。还有K-Prototype算法,可以对离散与数值属性两种混合的数据进行聚类,在K-prototype中定义了一个对数值与离散属性都计算的相异性度量标准。当然还有其它的一些算法,这里我 就不一一列举了。
K-means 与 GMM 更像是一种 top-down 的思想,它们首先要解决的问题是,确定 cluster 数量,也就是 k 的取值。在确定了 k 后,再来进行数据的聚类。而 hierarchical clustering 则是一种 bottom-up 的形式,先有数据,然后通过不断选取最相似的数据进行聚类。
感谢浏览,小白一枚,请多包涵。
参考网站:
[1]: https://www.cnblogs.com/baiboy/p/pybnc6.html
[2]: https://blog.csdn.net/u013719780/article/details/78413770
