白葡萄酒质量的聚类
一.关于聚类分析
1.1什么是聚类分析
聚类分析的主要目的是通过对数据集的合理划分来发现数据集的特征结构。利用聚类结果,我们能够提取数据集中隐藏的信息,对未来数据进行预测和分类。由聚类所生成的类或簇是一组数据对象的集合,且同类中的对象彼此相似,不同类间的对象彼此相异,是一种无监督学习的过程。
1.2聚类分析中的数据类型
连续型:
属性两个不同取值之间有无数多个其他取值,例如温度,高度等。这一类型的属性通常用数值(实数或整数)来表示,又称定量型变量。
离散型:
属性的取值是有限个,例如人的性别和民族等。这一类型的属性通常用有限个状态的字母,符号表示,但也可以是一组数值(如部分整数),又称定性型变量。
关联型:
源数据集只提供两个不同样本之间的相互关联关系,如相似度或距离等信息,通常用n*n维的矩阵来表示。
混合型:即属性取值类型包括以上各种数据类型,这种类型的数据在实际中也经常出现,相对来说,这种类型数据的处理也比较复杂。大多数混合型数据是指连续型和离散型数据的混合,即数值型和名词型数据的混合,而与关联型数据的混合较少。
1.3聚类模型
一般对聚类模型的设计有两大类:
基于层次的模型:
从树状图的角度来描述数据。
基于划分的模型:
从类原型的角度来描述数据。
上述两种类型的聚类算法设计内容通常包括三个方面:
1.样本与类间距离(相似度)的定义
2.聚类形成过程中的调整策略
3.聚类结束所需要满足的条件
K-均值和模糊C均值是对连续型数据基于划分进行的聚类方法。
1.4K均值与模糊C均值的异同
相同:
这两个方法都是迭代求取最终的聚类划分,即聚类中心与隶属度值。两者都不能保证找到问题的最优解,都有可能收敛到局部极值。
相异:
K均值:
一种硬聚类算法,隶属度只有两个取值0或1,提出的基本根据是“类内误差平方和最小化”准则。
模糊C均值:
一种模糊聚类算法,是k均值聚类算法的推广形式,隶属度取值为[0 1]区间内的任何一个数,提出的基本根据是“类内加权误差平方和最小化”准则。
模糊C均值是K均值方法的改进,算法的目标函数与K均值一致,区别在于目标函数中增加了模糊权重指数。
二.数据收集
2.1数据问题背景
用11个变量维度对白葡萄酒的质量进行分类。
样本个数:4898 个白葡萄酒样本
输入变量:
| # | 理化性质 | 字段名称 |
|---|---|---|
| 1 | 固定酸度 | fixed acidity |
| 2 | 挥发性酸度 | volatile acidity |
| 3 | 柠檬酸 | citric acid |
| 4 | 残糖 | residual sugar |
| 5 | 氯化物 | chlorides |
| 6 | 游离二氧化硫 | free sulfur dioxide |
| 7 | 总二氧化硫 | total sulfur dioxide |
| 8 | 密度 | density |
| 9 | PH值 | pH |
| 10 | 硫酸盐 | sulphates |
| 11 | 酒精度 | alcohol |
输出变量:
| # | 理化性质 | 字段名称 |
|---|---|---|
| 1 | 葡萄酒的质量 | quality |
2.2数据来源
UCI网站筛选
https://archive.ics.uci.edu/ml/datasets/Wine+Quality
2.3数据描述
输入变量:
根据理化实验得出的具体实数值。
输出变量:
基于感官的数据评分:0(很不好)-10(很好)分
网站对数据的描述:
这些数据集可以看作是分类或回归任务。等级是有序的,不平衡的(例如,普通葡萄酒比优质或劣质葡萄酒多得多)。离群点检测算法可用于检测少数优质或劣质葡萄酒。此外,我们不确定是否所有的输入变量都是相关的。因此,测试特征选择方法可能很有趣。
2.4如何将UCI数据转成MATLAB可用格式
参考:如何使用UCI数据集
我采用的是最常见的转成mat格式。
三.K-均值聚类
3.1原理
先预先指定聚类个数K。K均值算法将会初始给出K个随机聚类中心。为了得到“簇内距离小,簇间距离大”的聚类效果,K均值的做法是最终找到K个合适的聚类中心,来最小化平方误差:

为此K均值采取的是贪心的策略来求近似解,不断地把每个个体分配至距离它最近的那个聚类中心,然后移动每个聚类中心到它所代表的这个类的中心。然后算法重复:分配聚类中心,移动聚类中心。通过多次迭代来减小平方误差。
3.2算法
1.初始化K个聚类中心:
为了保证聚类中心位于确实有意义的位置,从样本中随机选择K个个体作为聚类中心。如果关于训练样本有一些先验知识,或已经预先知道了K个聚类中心的大概位置,也可以指定聚类中心位置。合适的初始设置将会极大改善最终聚类的效果,并提高聚类算法的效率。
注意:由于K均值算法的寻优采取的是贪心策略,较容易陷入局部最优,因此算法对于初始聚类中心的位置非常敏感,同样的训练样本集和同样的K,最终经常得到不同的聚类结果。
2为每个个体分配聚类中心
为了逐步减小平方误差值,我们为所有个体寻找到离它最近的聚类中心,并为此个体标注其所属的类。为下一步移动聚类中心至合适的位置打基础。
3.移动聚类中心
在设置完初始聚类中心后,每个簇内仅有一个个体,这是显然聚类中心就位于该簇的中心位置。但加入其他的个体后,聚类中心就需要移动其位置以保证自己位于簇的中心。
4.迭代
算法不断重复第2,3步,直到达到停止条件(用户设置的最大迭代次数,或者两次迭代并未改变聚类结果等)。
3.3实验过程及分析(重点)
代码一:
用MATLAB自带的K均值函数根据11个属性来进行聚类
MATLAB自带K均值函数介绍:
MATLAB函数Kmeans
使用方法:
[Idx,C,sumD,D]=Kmeans(X,K)
[…]=Kmeans(…,’Param1’,Val1,’Param2’,Val2,…)
各输入输出参数介绍:
输入:
X: NP的数据矩阵,N为数据个数,P为单个数据维度
K: 表示将X划分为几类,为整数
输出:
Idx: N1的向量,存储的是每个点的聚类标号
C: KP的矩阵,存储的是K个聚类质心位置
sumD: 1K的和向量,存储的是类间所有点与该类质心点距离之和
D: N*K的矩阵,存储的是每个点与所有质心的距离
[…]=Kmeans(…,‘Param1’,Val1,‘Param2’,Val2,…)
这其中的参数Param1、Param2等,主要可以设置为如下:
- ‘Distance’(距离测度)
‘sqEuclidean’ 欧式距离(默认时,采用此距离方式)
‘cityblock’ 绝度误差和,又称:L1
‘cosine’ 针对向量
‘correlation’ 针对有时序关系的值
‘Hamming’ 只针对二进制数据 - ‘Start’(初始质心位置选择方法)
‘sample’ 从X中随机选取K个质心点
‘uniform’ 根据X的分布范围均匀的随机生成K个质心
‘cluster’ 初始聚类阶段随机选择10%的X的子样本(此方法初始使用’sample’方法)
matrix 提供一K*P的矩阵,作为初始质心位置集合 - ‘Replicates’(聚类重复次数) 整数
clc,clear;
load winequality-white;
X=winequalitywhite1; %列向量变成行向量,4898*11矩阵
[x,y]=size(X);
opts = statset('Display','final');
K=3; %将X划分为K类
repN=50; %迭代次数
%K-mean聚类
[Idx,Ctrs,SumD,D] = kmeans(X,K,'Replicates',repN,'Options',opts);
%Idx N*1的向量,存储的是每个点的聚类标号
%打印结果
fprintf('划分成%d类的结果如下:\n',K)
for i=1:K
tm=find(Idx==i); %求第i类的对象
tm=reshape(tm,1,length(tm)); %变成行向量
fprintf('第%d类共%d个分别是%s\n',i,length(tm),int2str(tm)); %显示分类结果
end
分别分为3,4,5类别,迭代50次
K=3运行6次的结果:

K=4运行6次的结果:

K=5运行6次的结果:

虽然该数据集有11个等级(0-10分),即11种质量但因为数据的分类标签已知,且类别分布不均匀并不是所有等级都有,所以预判了一下K值,选择了K=3,4,5来进行实验。
运行速度的计算方法:
在函数前后用MATLAB自带记时:tic toc
结果准确度的计算方法:
对于验证研究来说,可以事先把样本本来所属的类别打标记,然后用聚类后的结果和标记做对比,有多少个样本和聚类结果一致,就计算相应的准确率。比方说,所有的样本标记和聚类结果一致,准确率就是100%。
3.4关于K均值的小结
K均值面临的问题以及解决办法:
1.它不能保证找到定位聚类中心的最佳方案,但是它能保证能收敛到某个解决方案(不会无限迭代)。
解决方法:多运行几次K-means,每次初始聚类中心点不同,最后选择方差最小的结果。
2.它无法指出使用多少个类别。在同一个数据集中,例如上图例,选择不同初始类别数获得的最终结果是不同的。
解决方法:首先设类别数为1,然后逐步提高类别数,在每一个类别数都用上述方法,一般情况下,总方差会很快下降,直到到达一个拐点;这意味着再增加一个聚类中心不会显著减少方差,保存此时的聚类数。我在实验的时候,也试了K=6,7,8发现K=5之后方差就没有出现大幅度下降,符合预判结果。
四.模糊C-均值聚类
4.1原理
模糊C均值的C跟K均值的K是一样的,指的是聚类的数目。F—Fuzzy是模糊的意思,指的是”一个事件发生的程度“。用在我们的聚类上面,第一条记录以怎样的概率或者说程度属于第一类,又以怎样的程度属于第二类等等。跟传统的聚类有所区别的地方就是,他改变了传统分类的时候非此即彼的一个现象,一个对象可以以不同的程度同时属于多个类。这个其实是跟我们的现实世界是更契合的。
4.2算法
输入:就是一个待聚类的数据集,每一个数据都有p个特征。
输出:是一个c行n列的矩阵U,c刚才提到是聚类数目,n是数据集中元素的个数,用这个矩阵就可以表示分类的结果,因为你看某一列,表示的就是这个元素对各个类的隶属程度,哪一个值最大,就说这个元素属于哪一类。
目标函数:
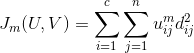
约束条件:某一个元素对所有类别的隶属程度的值加起来要等于1.
μij:隶属度值,元素j对类别i的隶属程度,
dij平方:欧氏距离下元素j跟中心点i之间的距离,整个表示的就是各个点到各个类的加权距离的和。
m:一个模糊化程度的参数,待会我们会提到它对算法性能的影响。=
聚类要达到的最终效果就是类内相似度最大,类间相似度最小,这个时候点和中心的加权距离之和就是最小的。所以我们我们只要使得目标函数取得最小值就可以了。所以最优解的的表达式就是:
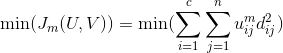
模糊C均值聚类算法是一个简单的迭代过程。在批处理方式运行时,FCM用下列步骤确定聚类中心ci和隶属矩阵U[1]:
1.用值在0,1间的随机数初始化隶属矩阵U,使其满足约束条件
2.计算c个聚类中心ci,i=1,…,c。
3.计算价值函数。如果它小于某个确定的阀值,或它相对上次价值函数值的改变量小于某个阀值,则算法停止。
4.计算新的U矩阵。返回步骤2。
上述算法也可以先初始化聚类中心,然后再执行迭代过程。由于不能确保FCM收敛于一个最优解。算法的性能依赖于初始聚类中心。因此,我们要么用另外的快速算法确定初始聚类中心,要么每次用不同的初始聚类中心启动该算法,多次运行FCM。
4.3实验过程及分析(重点)
代码:
输入:
data nm矩阵,n个样本数,每个样本的维度为m
n 类别数
options 41 矩阵
options(1):隶属度矩阵U的加权指数
options(2):最大迭代次数
options(3):隶属度最小变化量,迭代终止条件
options(4):每次迭代是否输出信息标志
输出:
center 聚类中心
U 隶属度矩阵
obj_fun 目标函数值
function[center,U,obj_fun]=FCMCluster(data,n,options)
%采用模糊C均值将数据集data分为n类
%用法
% 1 [center,U,obj_fcn]=FCMCluster(data,n,options);
% 2 [center,U,obj_fcn]=FCMCluster(data,n);
if nargin~=2 && nargin~=3
error('Too many or too few input arguments');
end
data_n=size(data,1);
in_n=size(data,2);
%默认参数
default_options=[2;100;1e-5;1];
%参数配置
%如果只输入前两个参数,选用默认的参数;如果参数个数小于4,其他选用默认参数
if nargin==2
options=default_options;
else
if length(options)<4
tmp=default_options;
tmp(1:length(options))=options;
options=tmp;
end
nan_index=find(isnan(options)==1);
options(nan_index)=default_options(nan_index);
if options(1)<=1
error('The exponent should be greater than 1!');
end
end
%将options 中的分量分别赋值给四个变量
expo=options(1);
max_iter=options(2);
min_impro=options(3);
display=options(4);
obj_fun=zeros(max_iter,1);
%初始化模糊分配矩阵
U=initfcm(n,data_n);
%主程序
for i=1:max_iter
[U,center,obj_fun(i)]=stepfcm(data,U,n,expo);
if display
fprintf('FCM:Iteration count=%d,obj_fun=%f\n',i,obj_fun(i));
end
%终止条件判别
if i>1
if abs(obj_fun(i)-obj_fun(i-1))<min_impro
break;
end
end
end
iter_n=i;
obj_fun(iter_n+1:max_iter)=[];
%
end
%%子函数 模糊矩阵初始化
function U= initfcm(n,data_n)
U=rand(n,data_n);
col_sum=sum(U);
U=U./col_sum(ones(n,1),:);
end
%%子函数 逐步聚类
function [U_new,center,obj_fun]=stepfcm(data,U,n,expo)
mf=U.^expo;
center=mf*data./((ones(size(data,2),1)*sum(mf'))');
dist=distfcm(center,data);
obj_fun=sum(sum((dist.^2).*mf));
tmp=dist.^(-2/(expo-1));
U_new=tmp./(ones(n,1)*sum(tmp));
end
%%子函数 计算距离
function out=distfcm(center,data)
out=zeros(size(center,1),size(data,1));
for k=1:size(center,1)
out(k,:)=sqrt(sum(((data-ones(size(data,1),1)*center(k,:)).^2)',1));
end
end
%输入:
load('winequality-white.mat');
data=winequalitywhite1;
options = [2;100;1e-5;1];
[center,U,obj_fcn] = FCMCluster(data,5,options);
plot(data(:,1),data(:,2),'o');
view(3);
hold on;
index1=find(U(1,:)==max(U));%找出划分为第一类的数据索引
index2=find(U(2,:)==max(U));%找出划分为第二类的数据索引
index3=find(U(3,:)==max(U));%找出划分为第三类的数据索引
index4=find(U(4,:)==max(U));%找出划分为第四类的数据索引
index5=find(U(5,:)==max(U));%找出划分为第五类的数据索引
这里的MATLAB自带函数的模糊矩阵初始化,是随机初始化的。
具体赋值步骤如下:
U = rand(cluster_n, data_n);
col_sum = sum(U);
U = U./col_sum(ones(cluster_n, 1), :);
上面就是它初始化的一个隶属度矩阵,
cluster_n行,data_n列。
即一列中从上到下表示每个样本隶属与每一类的隶属度。
然后在算法中不断迭代,
最后得到的还是如此大的一个矩阵,代表每个样本隶属与每一类的隶属度
然后选择最大的那个就是,它就属于那一类。
分类结果说明:

center:聚类中心表示的是每个类的平均特征,可以认为是这个类的代表点
index1:分出的第一类
index2:分出的第二类
index3:分出的第三类
obj_fcn:判别分类结束条件的目标函数值
options:输入
U:隶属度矩阵,4898个数据每个数据分别对三个类的隶属度,最终被分到隶属度最大的那个类钟
K=3运行6次的结果:

K=4运行6次的结果:

K=5运行6次的结果:

这里模糊C均值的时间是迭代一次的时间,而K均值的时间是迭代50次的总的时间。
4.4小结
1.由于不能确保FCM收敛于一个最优解。算法的性能依赖于初始聚类中心。因此,我们要么用另外的快速算法确定初始聚类中心,要么每次用不同的初始聚类中心启动该算法,多次运行FCM。
2.FCM算法需要两个参数一个是聚类数目C,另一个是参数m。一般来讲C要远远小于聚类样本的总个数,同时要保证C>1。对于m,它是一个控制算法的柔性的参数,如果m过大,则聚类效果会很次,而如果m过小则算法会接近HCM聚类算法。
五.两种聚类对比(分类结果,优点,缺点,各自适合用在什么时候)
1.速度:
在其他条件都相同的情况下,相同数据集,相同迭代次数,相同类别数量
K均值的速度更快。
2.目标函数:
在其他条件都相同的情况下,相同数据集,相同迭代次数,相同类别数量
模糊C均值的目标函数更优。
K均值:(实验获得)
优点:
1.原理简单,实现方便,收敛速度快;
2.聚类效果较优;
3.模型的可解释性较强;
4.调参只需要簇数k;
缺点:
1.k的选取不好把握;
2.对于不是凸的数据集比较难以收敛;
3.如果数据的类型不平衡,比如数据量严重失衡或者类别的方差不同,则聚类效果不佳;
4.采用的是迭代的方法,只能得到局部最优解;
5.对于噪音和异常点比较敏感。
模糊C均值:
优点:
1.优越于传统硬C均值聚类算法在于隶属度可以连续取值于 [0,1]区间,考虑到了样本属于各个类的“亦此亦彼”性,能够对类与类之间样本有重叠的数据集进行分类,具有良好的收敛性
2.复杂度低,易于实现。
缺点:
1.隶属度和为1的约束条件易造成它对对孤立点和噪声敏感
2.另一方面它本身是一种迭代下降的算法,使得它初始聚类中心敏感且不易收敛于全局最优。
K均值和模糊C均值算法的性能都依赖于初始聚类中心。因此,我们要么用另外的快速算法确定初始聚类中心,要么每次用不同的初始聚类中心启动该算法,多次运行。这是他们非常相似的地方。
选数据反思:
从算法的推导过程中可以看出,算法对于满足正态分布的数据聚类效果会很好。因此对于数据适当进行选择或者处理。
