1.三角分解(LU分解)
矩阵的LU分解是将一个矩阵分解为一个下三角矩阵与上三角矩阵的乘积。本质上,LU分解是高斯消元的一种表达方式。首先,对矩阵A通过初等行变换将其变为一个上三角矩阵。对于学习过线性代数的同学来说,这个过程应该很熟悉,线性代数考试中求行列式求逆一般都是通过这种方式来求解。然后,将原始矩阵A变为上三角矩阵的过程,对应的变换矩阵为一个下三角矩阵。这中间的过程,就是Doolittle algorithm(杜尔里特算法)。
转一个Tony Ma同学写的例子:
若AX=b是一个非奇异系统,那么高斯消元法将A化简为一个上三角矩阵。若主轴上没有0值,则无需交互行,因此只需进行第3类初等行变换(把第 i 行加上第 j 的 k 倍)即可完成此变换。例如 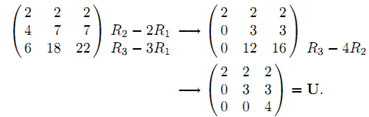
第3类行变换可以通过左乘相应的初等矩阵image实现,对上例来说进行的3个变换就是相应初等矩阵的乘积。注意最右边是一个下三角矩阵L 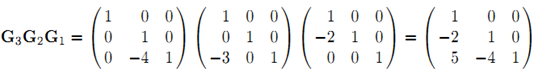
从而有G3G2G1A=UG3G2G1A=U,即A=G−11G−12G−13UA=G1−1G2−1G3−1U。因此A=LUA=LU,为一个下三角与一个上三角矩阵的乘积,因此称为LU分解。
注意:
1)U是高斯消元的结果,且对角线上是主元
2)L对角线上是1,对角线下面的元素image恰恰是在式1中用于消去(i,j)位置上元素的乘子。
LU分解常用来求解线性方程组,求逆矩阵或者计算行列式。例如在计算行列式的时候,A=LUA=LU,det(A)=det(L)det(U)det(A)=det(L)det(U)。而对于三角矩阵来说,行列式的值即为对角线上元素的乘积。所以如果对矩阵进行三角分解以后再求行列式,就会变得非常容易。
在线性代数中已经证明,如果方阵AA是非奇异的,即AA的行列式不为0,LU分解总是存在的。
2.QR分解
QR分解是将矩阵分解为一个正交矩阵与上三角矩阵的乘积。用一张图可以形象地表示QR分解: 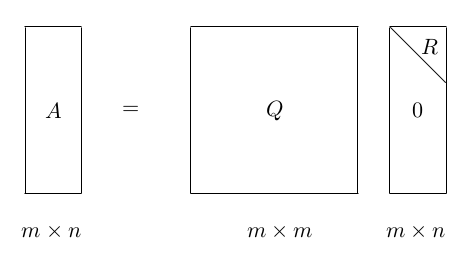
这其中, QQ为正交矩阵,QTQ=IQTQ=I,R为上三角矩阵。
实际中,QR分解经常被用来解线性最小二乘问题。
3.Jordan分解
每次看到Jordan分解,就想起当年考研的那段时光。控制原理里面,就有大段关于Jordan分解的内容。可惜当时矩阵分析没有学到位,线性代数里头又没有提到Jordan分解,所以理解起来那个费劲。
废话这么多,先来看看Jordan到底是个什么鬼:
我们将下面的k×kk×k阶方阵
称为Jordan块。同时,我们也将由若干个Jordan块组成的对角矩阵成为Jordan阵。
由Jordan块的定义不难看出,Jordan 阵与对角阵的差别仅在于它的上 (下)对角线的元素是0或1。因此,它是特殊的上三角阵。
为什么要进行Jordan分解呢?或者说,Jordan分解能解决什么问题呢?
我们先来复习一下,如果一个n阶方阵AA可以对角化,那么AA至少满足下列条件的一个:
1.AA有n个线性无关的特征向量。
2.AA的所有特征值的几何重数等于相应的代数重数,即qi=piqi=pi。
3.AA的极小多项式经标准分解后,每一项都是一次项,且重数都是1。
因为有的矩阵不可以进行对角化,那么我们可以对它进行Jordan分解,达到简化计算的目的。
4.SVD分解
关于SVD分解,前面已经有文章专门介绍了。
http://blog.csdn.net/bitcarmanlee/article/details/52068118