常见的特殊矩阵及分解

参考：维基百科

1、相似矩阵

两个 $n×n$ 矩阵 $A$ 与 $B$ 为相似矩阵，当且仅当存在一个 $n×n$ 的可逆矩阵 $P$ ，使得：
$P^{-1}AP=B$
$P$ 被称为矩阵 $A$ 与 $B$ 之间的相似变换矩阵.

相似变换下的不变性质：

两者的秩相等
两者的行列式值相等
两者的迹数相等
两者拥有同样的特征值，尽管相应的特征向量一般不同

2、正规矩阵

满足下列条件的矩阵都属于正规矩阵
$A^HA=AA^H$
注意，正规矩阵不一定可逆，如反对称矩阵就不可逆
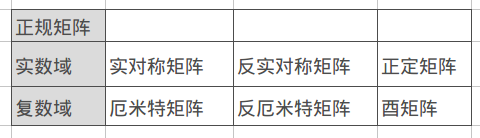
正规矩阵包括：
在这里插入图片描述

对角分解
任何一个矩阵一定和约当矩阵相似，即存在可逆矩阵 $P$ 使得 $P^{-1}AP=J$ ，对于一个实对称矩阵，一定存在可逆矩阵 $P$ 使得 $P^{-1}AP=\Lambda$ ，对这个结论进行推广，正规矩阵一定可以对角化，即存在酉矩阵 $U$ 使得
$U^HAU= {\Lambda}$
其中， $\Lambda$ 的对角线为 $A$ 的特征值.
设 $A$ 是 $n$ 阶正规矩阵，其特征值为 $\lambda_1, \lambda_2, ..., \lambda_n$ ，则

$A$ 是厄米特矩阵的充要条件是： $A$ 的特征值全是实数
$A$ 是反厄米特矩阵的充要条件是： $A$ 的特征值为零或纯虚数
$A$ 是酉矩阵的充要条件是： $A$ 的每个特征值 $\lambda_i$ 的模 $| \lambda_i |=1$

埃尔米特矩阵/厄米特矩阵（Hermitian matrix）
$A=A^H$
埃尔米特矩阵中每一个第i行第j列的元素都与第j行第i列的元素的复共轭

埃尔米特矩阵主对角线上的元素都是实数的，其特征值也是实数。对于只包含实数元素的矩阵（实矩阵），如果它是对称阵，即所有元素关于主对角线对称，那么它也是埃尔米特矩阵。也就是说，实对称矩阵是埃尔米特矩阵的特例

实对称矩阵
$A=A^T$

反厄米特矩阵/反埃尔米特矩阵

反实对称矩阵/ 斜对称矩阵（`skew-symmetric matrix`）

$A^T=-A$

行列式
$\operatorname { det } ( A ) = \operatorname { det } \left( A ^ { T } \right) = \operatorname { det } ( - A ) = ( - 1 ) ^ { n } \operatorname { det } ( A )$

斜对称矩阵的主对角线元素必是0，所以其迹数为零
斜对称矩阵自身相乘的积是对称矩阵
任意矩阵 $A$ ， $A^T-A$ 是斜对称矩阵
若 $A$ 是斜对称矩阵， $x$ 是向量， $x^T A x$ = 0，即二次型为0

正交矩阵（orthogonal matrix）
正交矩阵是一个方块矩阵 $Q$ ，其元素为实数，而且行与列皆为正交的单位向量，使得该矩阵的转置矩阵为其逆矩阵：
$Q ^ { T } = Q ^ { - 1 } \Leftrightarrow Q ^ { T } Q = Q Q ^ { T } = I$
正交矩阵的行列式值必定为+1或-1，因为：
$1 = \operatorname { det } ( I ) = \operatorname { det } \left( Q ^ { T } Q \right) = \operatorname { det } \left( Q ^ { T } \right) \operatorname { det } ( Q ) = ( \operatorname { det } ( Q ) ) ^ { 2 } \Rightarrow | Q | = \pm 1$

下面是一些重要的性质：

作为一个线性映射（变换矩阵），正交矩阵保持距离不变，所以它是一个保距映射，具体例子为旋转与镜射
行列式值为+1的正交矩阵，称为特殊正交矩阵，即我们常说的旋转矩阵
行列式值为-1的正交矩阵，称为瑕旋转矩阵，瑕旋转就是旋转加上镜射。
所有 $n \times n$ 正交矩阵形成一个群 $O(n)$ ，称为正交群。亦即，正交矩阵与正交矩阵的乘积也是一个正交矩阵。
所有特殊正交矩阵形成一个子群 $SO(n)$ ，称为特殊正交群。亦即，旋转矩阵与旋转矩阵的乘积也是一个旋转矩阵。

Cholesky分解
三角分解中的一种
如果 $A \in C^{n \times n}$ 是正定的厄米特矩阵，则存在下三角矩阵 $G$ 使得
$A=GG^H$
在求解最小二乘 $Ax=b$ 时，因为 $A$ 是超定矩阵，所以先要转换成正定的厄米特矩阵才能使用Cholesky分解，即 $A^TAx=A^Tb$ .

QR分解，分解成正交矩阵和一个上三角矩阵
2) LU分解，分解为一个下三角矩阵和一个上三角矩阵的乘积
- 用于计算行列式，|A|=|L||R|
- 求解线性方程组，使用替代法求解
- 求逆矩阵
1. Cholesky分解，指将一个正定的Hermite矩阵分解成一个下三角矩阵与其共轭转置之乘积
  - 效率是LU的两倍
2. 奇异值SVD分解，任何一个矩阵（不限方阵）都可以实现SVD分解
  参考《矩阵分析》，整明白了奇异值分解，为什么A=UDV^T中的V每一列对应一个特征值的特征向量（P74）
3. 特征值EVD分解，