一、VC问题&其NPC证明
定义:对于给定的一个图G和一个正整数k是否存在小于等于k个顶点,使得这些点所关联的边能够覆盖整个图G;
在这里我们由已知的3SAT规约到VC问题(在之前已经证明3SAT是NPC问题)
![]()
这里的任意Ci满足|Ci|=3这个条件,下面我们根据3SAT的条件找出一个变换使得其为VC问题;
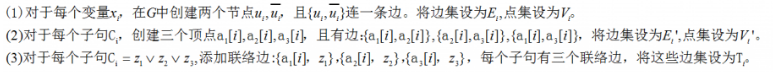
在这里举一个例子便于理解(给出如下3SAT实例,将其转化为顶点覆盖(VC)问题):

根据上述的的构造过程,我们可以将其转化为如下的VC实例:
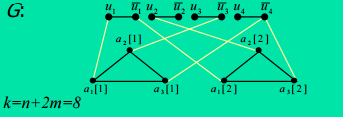
由上图G所示要想覆盖各个图所有的边直线边的顶点至少选择一个,故总个数为n个,对于覆盖三角形(子句)的边
其顶点至少选择两个有m个子句,故选择的顶点为2m个。因此要想覆盖这个图k至少为n+2m;
(在这里如果一条联络边被选择,其对应的三角形只能选择另外两个顶点在覆盖其对应的两条联络边)
由此我们得出了3SAT到VC的一个变换,下面证明此变换是可以在多项式时间内完成的:
在这里一共增加了n+3m+3m条边,显然是可以在多项式时间内构造完成,故满足多项式规约;
最后证明此规约过程是等价的:(前者为真时满足后者,后者为真时满足前者)

对于3SAT中的每一个子句其一定覆盖一条联络边,只需选出这条联络边未覆盖的顶点即可满足VC问题;
![]()
因为与每个三角形部件对应的三条联络边至少有一个被点覆盖所以每个三角形对应的子句为真,故满足3SAT;
二、团问题&独立集(IS)问题
由上述证明我们已经知道VC问题是NPC问题,现在根据此条件和以下定理,我们很容易证明团问题和IS问题也为NPC问题。
(注:本质上这三个问题是等价的,彼此之间可以相互转化)
对于任意一个图G=(V,E),假设V ' 是V的一个子集,对于以下3个条件彼此之间是等价的:
1)V '是图G的一个顶点覆盖; 2)V - V ' 是G的一个独立集; 3)在G的补图中V - V ' 是一个团;
显然团问题和IS问题都是可以在多项式时间内验证的,故它们都是NP问题;
下面证明IS问题是NPC问题:(从VC问题转换)
设有一个顶点覆盖实例(G,k)有一个k的顶点覆盖,则G中的任意一条边其端点至少有一个被选择,至多有一个
在V - S中 (边的顶点要么都在S中要么有一个在S中,亦或是都不在V - S中或有一个在V - S中)即V - S中的任意
两个点都没有边,所以V - S为独立集;
下面证明团问题是NPC问题:(从IS问题转换)
在独立集(G,k)中,有一个大小为k的独立集,S中任意两个顶点无边,则对于其补图中任意两个顶点都存在边,
故此补图为一个团;(独立集的补图是团)
