A Road to Deep Neural Networks

作者：XU Ruilin
Master's degree candidate, major in pattern recognition and intelligent system.

导语：人工神经网络（Artificial Neural Network, ANN）简称神经网络（Neural Network, NN），是一个大量简单元件相互连接而成的复杂网络，具有高度的非线性，能够进行复杂的逻辑操作和非线性关系实现的系统。本文从浅层到深层对人工神经网络进行了简要总结。主要内容来自Andrew Ng的Coursera深度学习系列课程，符号记法也采用Andrew Ng的记法。

1 从生物学而来的M-P神经元模型

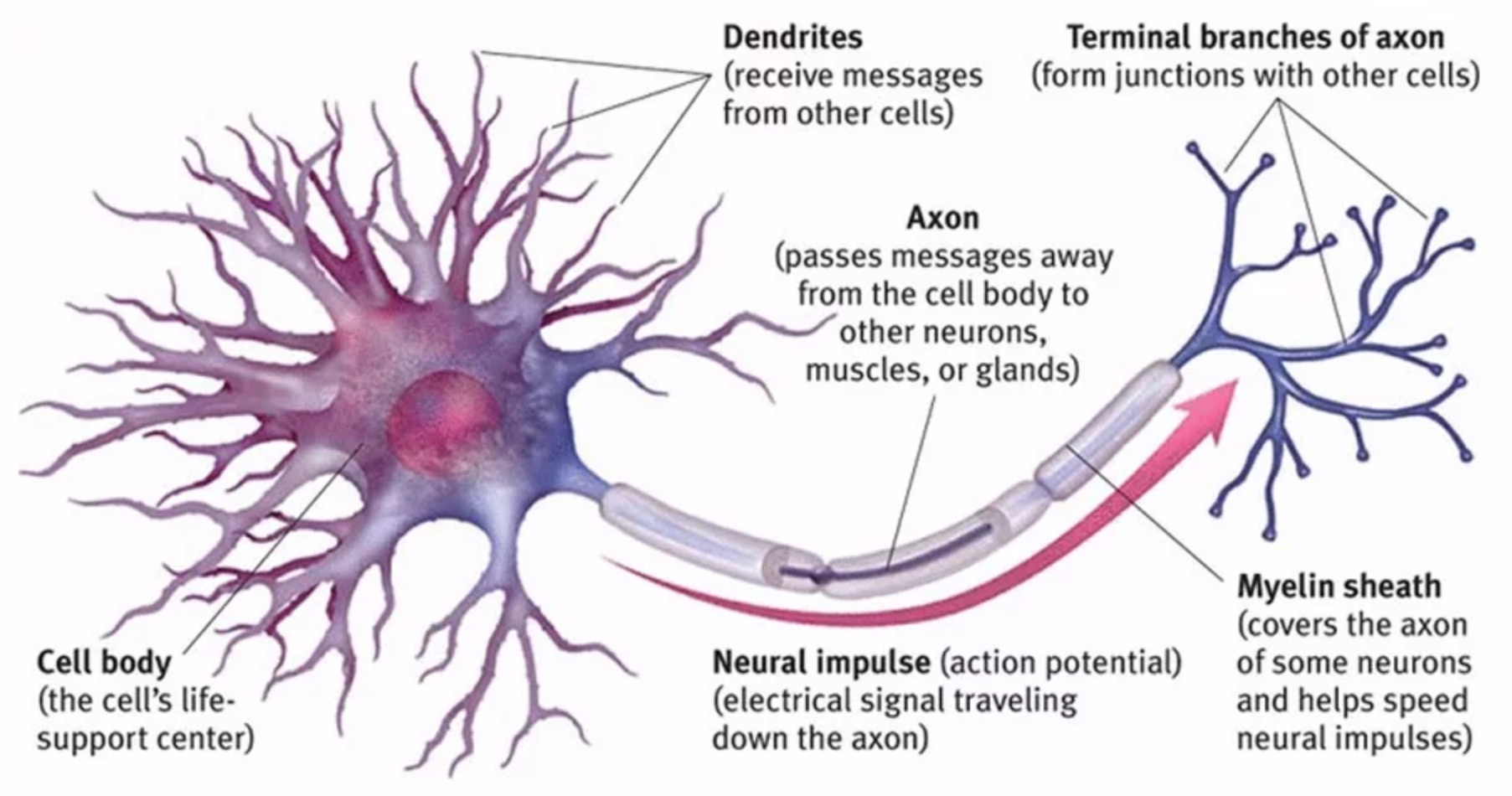
在高中二年级的生物课上，我们学过神经元是一个由“树突——胞体——轴突——轴突末梢”组成的细胞（Fig.1）。1943年，Warren McCulloch和 Walter Pitts参考生物神经网络结构，提出了M-P神经元模型。

Figure 1. 生物的神经元结构
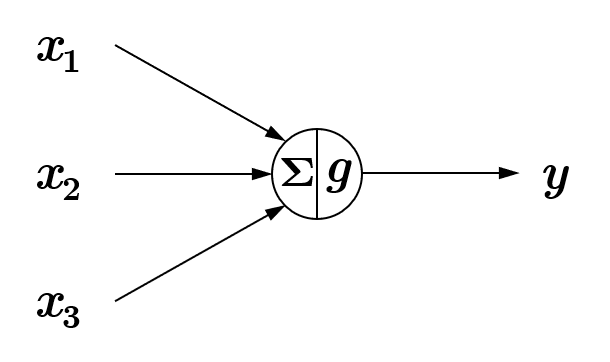
M-P神经元模型的结构如 Fig.2 所示， $x_1, x_2, x_3$可以视作为神经元树突传入的电信号，三个箭头可以视作为树突，中间的圆圈可以视作为神经元胞体，从圆圈出来的箭头可以视作是轴突， $y$可以视作为神经元传出的电信号（神经冲动）。电信号 $x_1, x_2, x_3$在胞体中的 $\Sigma$单元进行线性相加处理。

Figure 2. M-P神经元的结构
初等数学告诉我们， 在表达能力上，有限次连续线性变换与一次线性变换相同 [注1] 。如果只进行线性变换，不管网络的规模多模庞大，有多少个神经元节点，其表达能力与一个神经元没有区别。

注1 设有$f_1(x)=a_1x+b_1, f_2(x)=a_2x+b_2,f_3(x)=a_3x+b_3;$
ensp; 则
\[ \begin{align} F(x)&=f_1 \circ f_2 \circ f_3=a_1(a_2(a_3x+b_3)+b_2)+b_1)\\ &=a_1(a_2a_3x+a_2b_3 +b_2)+b_1\\ &=(a_1a_2a_3)x+(a_1a_2b_3+a_1b_2+b_1); \end{align} \]
记 $A=a_1a_2a_3, B=a_1a_2b_3+a_1b_2+b_1, $则$F(x)=Ax+B.$

同理，递归到 $f_n$也是一个线性变换。
因此，在神经元胞体中引入了非线性函数 $g(\cdot)$来进行非线性变换，用以解决更为复杂的非线性问题。在M-P神经元模型中，作者为了模拟神经元的膜电位阈值被激活的过程，使用符号函数 ${\mathrm{sgn}}\;(x)$作为非线性函数，此处不做赘述。

2 单层神经网络

在M-P神经元中，显然电信号刺激$x_1, x_2, x_3$的强度是不同的，在神经网络模型中，我们采用参数（parameters）$w_1, w_2, w_3$来表示这种强度，$w$代表权重（weights）。同时，引入偏置（bias）项参数$b$，来表示神经元细胞膜电位阈值 [注2]。

注2 参数$w$的意义是比较易于理解的，而关于偏置$b$（在统计学中也称偏差），分两个角度解释——
从生物学角度看，在生物体中，神经元的兴奋程度超过了某个限度，也就是细胞膜去极化程度超过了某个阈值电位时，神经元被激发而输出神经脉冲。人工神经网络借鉴了这种阈值特性，神经元激活与否取决于某一阈值，即只有其输入综合超过阈值时，神经元才会被激活，这个阈值体现在线性单元中，就是偏置项$b.$
从数学角度看，神经网络模型的初衷是解决分类（Classification）问题（当然现在的神经网络也可以解决回归/Regression问题）。以最简单的二分类问题为例，就是用一条直线将两类样本点分开，如果没有偏置项$b$，那么用于分类的所有直线都只能通过原点，这显然是不能很好地解决分类问题的（神经网络中的偏置项b到底是什么[EB/OL].(2018-07-05)[2020-02-19]）。

应用新的参数表示法后，神经网络模型变成了如 Fig.3 所示的结构，在一些文献中称其为感知机（Preception）模型。若记$x=[x_1, x_2, x_3]^\top$，$w=[w_1, w_2, w_3]^\top$，则线性单元可以表述为$w^\top x+b$，$g(\cdot)$是非线性函数。

Figure 3. 感知机模型
观察这个模型可以发现（如果有机器学习算法基础），我们知道在分类问题中常用的 逻辑斯蒂回归（Logistic Regression）方法与上述模型具有相同的结构。

2.1 从逻辑斯蒂回归说起

我们以一个简单的二分类问题为例来介绍逻辑斯蒂回归。假如要判断$x$是不是新型冠状病毒COVID-19，用$y=1$表示“是”，$y=0$表示“不是”，那么数据对$(x,y)$就可以表示这个实例。假设输入$x$的特征有$x_1,x_2,\cdots, x_n$共$n$个，分别表示$n$种检测方法测得的指标值，记$x=[x_1,x_2,\cdots,x_n]^\top$。我们对采纳这$n$种检测方法的权重为$w_1,w_2,\cdots,w_n$，记$w=[w_1,w_2,\cdots,w_n]^\top$，样本偏差为$b$。输出的结果记为$\hat{y}$，表示$x$是新冠病毒的概率，用条件概率表达为$P(y=1|x)$。
在经过计算$z=w^\top x+b$后，由于$z$并不一定收敛于区间$[0,1]$内，因此要对$z$进行归一化（Normalization）处理。在Logistic Regression中，使用Sigmoid函数进行归一化。
Sigmoid函数（Fig.4）定义为
\[ \begin{align*} \sigma(z)=\frac{1}{1+e^{-z}} \end{align*} \]

Figure 4. Sigmoid函数
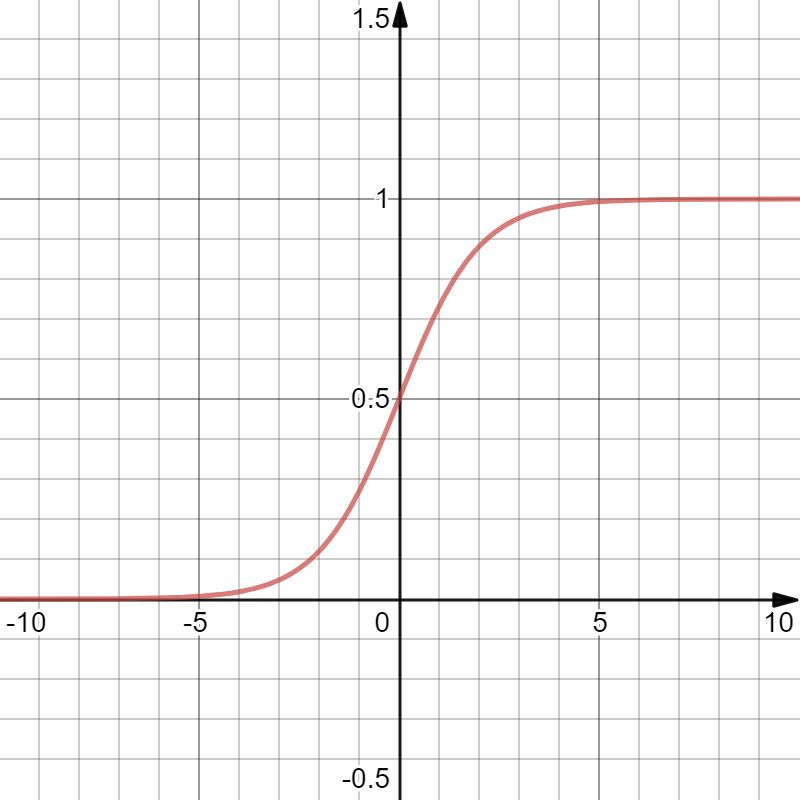
Sigmoid函数就是神经网络模型中非线性函数 $g(\cdot)$的一种，在神经网络中，我们称这种非线性函数为 激活函数（Activation Function），这样，例子中的问题就变成了

\[ \hat{y}=g(z)=g(w^\top x+b), {\rm where}\; g(z)=\sigma(z)=\frac{1}{1+e^{-z}}; \]
\[ {\rm given\;}(x,y),\;{\rm want}\;\hat{y}\approx y. \]
那么，我们如何评价我们分类模型的效果呢？在统计机器学习中，对于单个样本数据，我们常用损失函数（Loss Function）来评估机器学习算法。在Logistic Regression中，LOSS函数为[注3][注4]
\[ \mathcal{L}(\hat{y},y)=-y\log \hat{y}-(1-y)\log (1-\hat{y}). \]

注3 在上式中，对数$\log$应为以自然常数$e=\lim_\limits{n \to \infty}(1+\frac{1}{n})^n$为底的自然对数，在数学教材中习惯记为$\ln x.$
此外，关于未指明底数的$\log$用法，在数学中一般指常用对数$\lg x$（底为10）；在计算机科学中（如微机原理、数据结构、算法等）一般指底为2的对数$\log _2 x$；在编程语言中一般指自然对数$\ln x.$（奇怪的知识增加了！）

注4 为什么损失函数长这个样子？
在Logistic Regresion中，我们的目标是要使$\hat{y}$尽可能地接近$y$。前面我们说到，$\hat{y}=P(y=1|x)$，那么$1-\hat{y}=P(y=0|x).$
由于这是一个二分类问题，\[ y \in \left \{0,1\right \} \]，因此，经过代数变幻的鬼斧神工我们将上述两个条件概率合并成一个表达式

\[ P(y|x)=\hat{y}^y(1-\hat{y})^{1-y} \]
我们验证一下就可以知道，当$y=1$时，
\[ P(y=1|x)=\hat{y}^1(1-\hat{y})^0=\hat{y}; \]
当$y=0$时，$P(y=0|x)=\hat{y}^0(1-\hat{y})^1=1-\hat{y}.$
由于$\log x$（这里指$\ln x$）是严格单调递增函数，则$\log P(y|x)$的单调性与$P(y|x)$完全一致。
又因为
\[ \log P(y|x)=y\log \hat{y}+(1-y)\log (1-\hat{y}) \]
要使$P(y|x)$最大，就是使损失（LOSS）最小，因此取负号得
\[ \mathcal{L}(\hat{y},y)=-\log P(y|x)=-y\log \hat{y}-(1-y)\log (1->\hat{y}). \]

2.2 用矩阵描述问题

如果要编程来实现前述的单样本Logistic Regression问题，我们要写一个for循坏——

# Python 3
# input w,x,b
for i in range(n):
    z += w[i]x[i]
z += b

实际上，在之前的描述中，我们已经采用了一种记法，记\[x=[x_1,x_2,\cdots,x_n]^\top \]，记\[w=[w_1,w_2,\cdots,w_n]^\top \]，然后用\[w^\top x\]来代替\[\Sigma ^n_{i=1}w_ix_i\]的过程。在Python 3中，我们通过调用第三方库numpy，就可以用一行代码z = np.dot(w.T,x) + b解决上面的问题。
那么如果有$m$份病毒样本，这个检测问题又该如何表示？
现有$m$份病毒样本$x^{(1)},x^{(2)},\cdots,x^{(m)}$，其中每份病毒样本的$n$个特征为$x^{(i)}=[x_1^{(i)},x_2^{(i)},\cdots,x_n^{(i)}]^\top$，上标$^{(i)}$表示第$i$份样本，下标$_j$表示第$j$个特征，例如$x_1^{(3)}$表示第3份病毒样本的第1个特征。
那么，我们的问题变成了
\[ \hat{y}^{(i)}=g(z^{(i)})=g(w^\top x^{(i)}+b), {\rm where}\; g(z)=\sigma(z)=\frac{1}{1+e^{-z}}; \]

\[ {\rm given\;}\left \{ (x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),\cdots,(x^{(m)},y^{(m)})\right \},\;{\rm want}\;\hat{y}^{(i)}\approx y^{(i)}. \]
也就是把一个样本的Logistic Regression重复$m$遍。我们现在从编程的角度来思考一下，对于$m$份，每份有$n$个特征的样本，要如何实现？
显然，我们要用2个for循环才能实现$m$个样本，以及每个样本$n$个特征的线性计算。

# Python 3
import numpy as np

def sigmoid(x):
    return 1/(1 + np.exp(-x))

# input: w,x,b

for i in range(m):
    for j in range(n):
        z += w[j] * x[i,j]
    z += b
    y_hat = sigmoid(z)
    z = 0

这种方法的时间复杂度为$O(n^2)$，是一个P问题，还是过于复杂。我们考虑将前述的行向量乘列向量的做法推广到$m$个样本的情况下——
记$w=[w_1,w_2,\cdots,w_n]^\top$（此时的权重还不会随样本变化，因此每个样本在神经网络中施加的刺激强度都是同等的，等看完2.3节之后就知道权重变化时是什么情况了），记输入为矩阵$X$，$X$为
\[ X = {\begin{bmatrix}x^{(1)}_1 & x^{(2)}_1 & \cdots & x^{(m)}_1\\ x^{(1)}_2 & x^{(2)}_2 & \cdots & x^{(m)}_2\\ \vdots & \vdots & \quad & \vdots\\ x^{(1)}_n & x^{(2)}_n & \cdots &x^{(m)}_n\\ \end{bmatrix}}_{n \times m} \]
我们用本科二年级学过的矩阵乘法就可以知道
\[ w^\top X = {\begin{bmatrix} w_1 & w_2 & \cdots & w_n \end{bmatrix}}_{1 \times n}{\begin{bmatrix} x^{(1)}_1 & x^{(2)}_1 & \cdots & x^{(m)}_1\\ x^{(1)}_2 & x^{(2)}_2 & \cdots & x^{(m)}_2\\ \vdots & \vdots &\quad &\vdots\\ x^{(1)}_n & x^{(2)}_n & \cdots &x^{(m)}_n\\ \end{bmatrix}}_{n \times m} \]
也即
\[ w^\top X = {\begin{bmatrix} \Sigma ^n_{i=1}w_ix^{(1)}_i & \Sigma ^n_{i=1}w_ix^{(2)}_i & \cdots & \Sigma ^n_{i=1}w_ix^{(m)}_i \end{bmatrix}}_{1 \times m} \]
继而
\[ Z={\begin{bmatrix} z_1 & z_2 & \cdots & z_n \end{bmatrix}}_{1 \times m}=w^\top X+{\begin{bmatrix} b & b & \cdots & b \end{bmatrix}}_{1 \times m} \]

\[ Z={\begin{bmatrix} \Sigma ^n_{i=1}w_ix^{(1)}_i+b & \Sigma ^n_{i=1}w_ix^{(2)}_i+b & \cdots & \Sigma ^n_{i=1}w_ix^{(m)}_i+b \end{bmatrix}}_{1 \times m} \]
这在Python 3中可以写成Z = np.dot(w.T,X) + b[注5]。这种直接加常数$b$的操作，就是将$b$reshape到与之相加的矩阵维度再相加，Python中称之为广播（Broadcasting）。

注5 为什么numpy中应用矩阵操作可以降低时间复杂度？
实际上，在numpy算法底层，运用了一种称为单指令多数据流（Single Instruction Multiple Data, SIMD）指令的操作，它使得多维数据可以在CPU中进行并行计算，因此比for循环低效占用CPU的计算效率更高。

这里对$m$和$n$在神经网络中的意义再作进一步解释：$n$是每个样本的特征总数，决定了我们的神经网络有多少个输入。$m$是样本总数，决定了我们的神经网络要运行多少次。
到目前为止，我们在前文所做的工作，也就是在神经网络中进行的从输入到输出的过程，成为前向传播（Forward Propagation）。
这时，在$m$个样本的情况下，第$i$个样本的损失函数就变成了
\[ \mathcal{L}(\hat{y}^{(i)},y^{(i)})=-y^{(i)}\log \hat{y}^{(i)}-(1-y^{(i)})\log (1-\hat{y}^{(i)}); \]
我们用代价函数（Cost Function）来衡量共$m$个样本的效果，记
\[ \mathcal{J}(\hat{y},y)=\frac{1}{m}\Sigma _{i=1}^m \mathcal{L}(\hat{y}^{(i)},y^{(i)}); \]
又$\hat{y}=\sigma(w^\top x+b)$，而$x,y$是样本数据[注6]，所以代价函数也可以改写为
\[ \mathcal{J}(w,b)=\frac{1}{m} \Sigma _{i=1}^m \mathcal{L}(\hat{y}^{(i)},y^{(i)}). \]

注6 在算法中，学习者必须明确区分代数符号表述的对象是变量（Variable）还是参量/参数（Parameter）。实际上，变量和参量要根据面对的问题进行具体分析。例如上例中，$w,b$是参量，$x,y$是变量。
读者可以尝试分析，在本文介绍逻辑斯蒂回归和梯度下降两个算法中所用的代数符号，哪些是参量？那些是变量？

2.3 让模型不断优化

我们之前已经介绍了损失函数$\mathcal{L}(\hat{y},y)$是对分类结果的度量。那么，如何让LOSS尽可能的小？也就是使$\hat{y}$更接近$y$，即$P(y|x)$最大？

2.3.1 一点数理统计和微分操作

在本科二年级，我们在数理统计中的参数估计部分学过极大似然估计（log-likelihood）方法。我们先从一个样本开始——
\[ \mathcal{L}(\hat{y},y)=-y\log \hat{y}-(1-y)\log (1-\hat{y}) \]
在这个问题中，我们估计的对象是$\hat{y}$，用极大似然估计，求导有
\[ \frac {\mathrm{d}\mathcal{L}(\hat{y},y)}{\mathrm{d}\hat{y}}=-\frac{y}{\hat{y}}+\frac{1-y}{1-\hat{y}} \]
接着令$\frac {\mathrm{d}\mathcal{L}(\hat{y},y)}{\mathrm{d}\hat{y}}=0$，求使$\mathcal{L}(\hat{y},y)$取极小的$\hat{y}$即可。
这种表达实际上与我们的本科数学知识不太一致，实际上，$\hat{y}$是关于$w,b$的函数，那么我们将损失函数改写为$\mathcal{L}(w,b)$，然后对两个参数$w,b$求偏导数，然后采用同样的极大似然估计方法，令——
\[ \frac {\partial\mathcal{L}(w,b)}{\partial w}=0,\frac {\partial\mathcal{L}(w,b)}{\partial b}=0 \]
接着取最优估计的参数$w,b$就完成了这个过程[注7]。

注7 本文中的$w,b$都是向量，在数学上应当采用矢量运算。本文的记法并不严格符合数学规则，仅说理用。

2.3.2 梯度下降

和对导数表烂熟于心的我们不同，计算机对$f(x)=x^2$，则$f^\prime (x)=2x$这类符号计算并不十分擅长。相反，计算机相比人脑在计算方面的最大优势在于数值计算，也就是说，在求导问题上，计算机更喜欢求函数在某一个点的导数值，而不是求导函数表达式。我们在前文提到的一个简单的求导（当让如果函数复杂来求显式解析解可能也不那么简单）取0的步骤，在计算机中需要像微分的定义一样一步步求一个精度阈值内的近似解（阅读参考）。
在我们参数估计问题中，计算机不能一步找到这个最优的$w,b$，那么，有没有一种办法，可以让计算机更快地找到$w,b$，更迅速地下降到$\mathcal{L}(w,b)$的最低点呢？
如果我们对多元函数微分学还有那么一点残存的记忆，那么我们可以知道，函数的方向导数在梯度方向上取得最大。换言之，函数沿着梯度方向下降最快。借由这一点，我们给出了梯度下降（Gradient Descent）算法。
Fig.5 是梯度下降的图示。在多元函数微分学中，我们用$\nabla \mathcal{J}(w^{(0)},b^{(0)})$表示函数在$(w^{(0)},b^{(0)})$点处的梯度。梯度下降算法用递归表示就是——
\[ (w^{(i+1)},b^{(i+1)})=(w^{(i)},b^{(i)})-\alpha \nabla \mathcal{J} (w^{(i)},b^{(i)}) \]
式中$\alpha$表示每次下降的步长。

Figure 5. 梯度下降
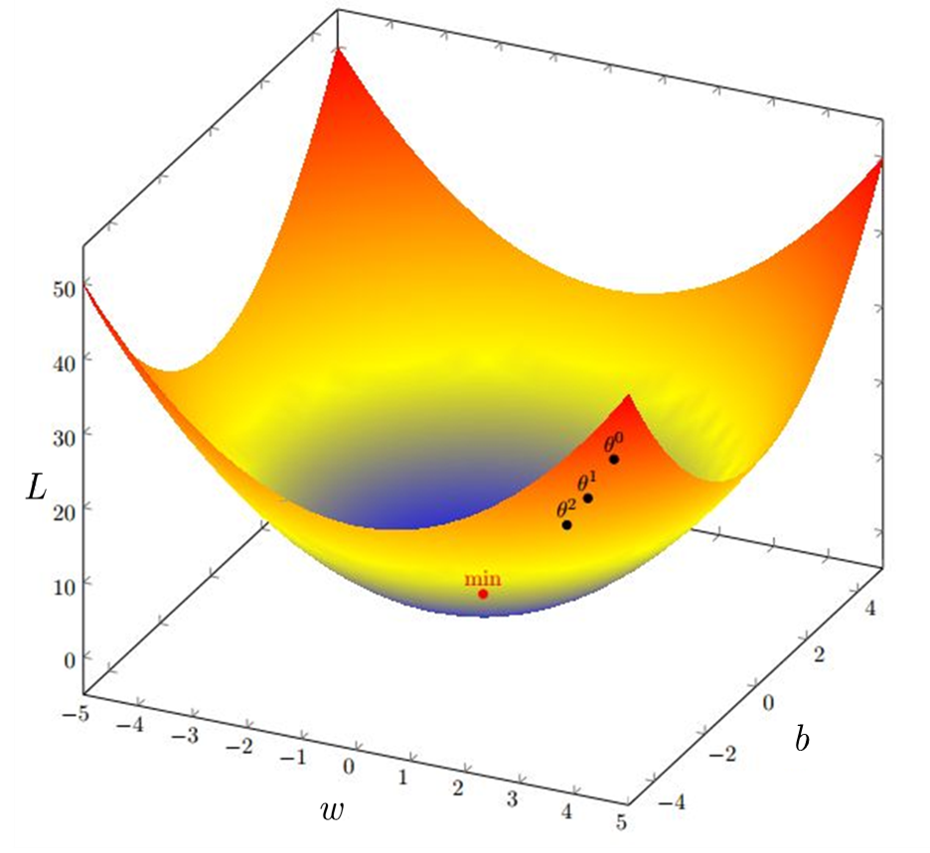
显然，如果只有一个样本，那么梯度下降只进行一次，其效果当然不会特别好，这也就是为什么我们需要大量样本的原因。
在 $m$个样本的情况下，我们进行 $m$次迭代，就能准确快速地估计出最优参数 $(w,b)$的值。我们发现此时 $(w,b)$是随样本 逐代变化的，这就可以理解为一种简单的 学习机制，我们前述的步长 $\alpha$也被称为 学习率（Learning Rate）我们重复用 $m$个样本投入神经网络的过程，在机器学习中，就是 训练（Training）。到这里，我认为可以说我们的神经网络具备了一种初级的智能要素。
当然，梯度下降也可能存在陷入局部最优的问题，所以一般在初始化梯度下降时，我们会根据经验确定参数初值 $(w^{(0)},b^{(0)})$，也可能把它们定为随机数或者零向量，以及学习率 $\alpha$的大小。也就是说，从什么地方开始下降（ $w,b$），还有每一步跨越多少（ $\alpha$）非常重要。关于梯度下降，你也可以在这里找到参考。
我们现在用计算图（ Fig.6）回顾一下前文所述的过程。从左到右计算分类结果的过程（ 逻辑斯蒂回归）称为 前向传播（Forward Propagation）过程；从右到左通过 求导（这里多元函数求偏导数应当遵循链式法则）估计最优参数的过程（ 梯度下降）称为 后向传播（Backward Propagation）过程。通过前向传播和反向传播，我们就构建了一个比较完整的、由单个神经元组成的神经网络。

Figure 6. 前向传播与反向传播
读者可以自行思考怎么把后向传播（梯度下降）过程也用矩阵描述，然后编程实现。当然，如果存在困难，记得善用搜索引擎和代码托管平台。

3 多层神经网络

这种单层神经网络显然只能解决线性分类任务（Logistic回归的特性导致的），不能解决现实的复杂问题。不过，我们不妨回到我们开始的地方，想想生物是怎么做的。我们在高中生物中学过，许多形态相似的细胞及细胞间质构成了生物组织，比如上皮组织、结缔组织等。这些生物组织以及可以实现一些简单的人体机能。所以，我们当然也可以把神经元组织起来去解决更复杂的问题。

3.1 两层神经网络

我们给神经网络再加3个神经元，这样它就变成了有3个输入特征$x_1,x_2,x_3$，4个神经节点，1个输出$\hat{y}$的神经网络结构（Fig.7）。

Figure 7. 两层神经网络结构
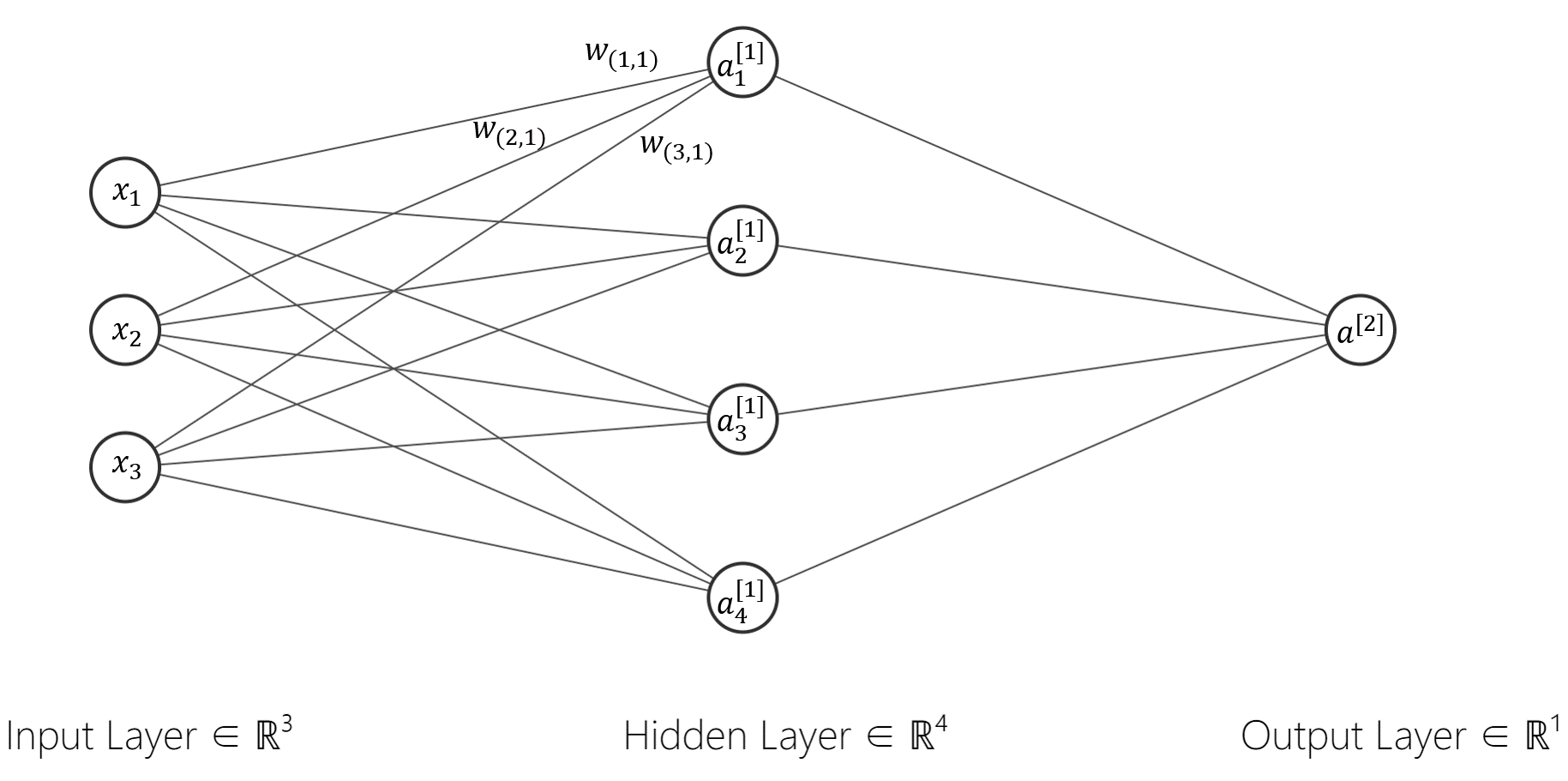
我们将从左到右的节点分为三层，第0层，用上标 $^{[0]}$表示，称为 输入层（Input Layer）;第1层，用上标 $^{[1]}$表示，称为 隐藏层（Hidden layer）；第2层，用上标 $^{[2]}$表示，称为 输出层（Output Layer）。在这里用 $a^{[1]}_1$表示第1层（隐藏层）的第1个神经元进行的运算后的输出，用 $a^{[2]}$表示输出层神经元的运算后的输出 $\hat{y}$。
现在网络中的所有连接（连线）都对应着自己的权重 $w$，每层都对应一个自己的偏差 $b$（层内的节点公用一个参数 $b$）。我们将传入每个神经元的 $w$和 $b$记为一组。例如，以隐藏层第1个神经元为例， $w_1^{[1]}=[w_{(1,1)}^{[1]},w_{(2,1)}^{[1]},w_{(3,1)}^{[1]}]^\top$就相当于原来单层神经网络中的 $w$，记神经元输入为 $a^{[0]}=x=[x_1,x_2,x_3]^\top$类似地，我们的计算就成为了——
\[ a^{[1]}_1=\sigma({w^{[1]}_1}^\top a^{[0]}+b^{[1]}); \]
对应有 $a^{[1]}_2=\sigma({w^{[1]}_2}^\top a^{[0]}+b^{[1]})$，其中 $w_2^{[1]}=[w_{(1,2)}^{[1]},w_{(2,2)}^{[1]},w_{(3,2)}^{[1]}]^\top .$
第2层为
\[ a^{[2]}=\sigma({w^{[2]}}^\top a^{[1]}+b^{[2]})=\hat{y}; \]
其中 $w^{[2]}=[w_1^{[2]},w_2^{[2]},w_3^{[2]},w_4^{[2]}]^\top,a^{[1]}=[a^{[1]}_1,a^{[1]}_2,a^{[1]}_3,a^{[1]}_4]^\top.$
如果也扩充到 $m$个样本（每个样本 $n$个特征）的情况，仍然用上标 $^{(i)}$表示第 $i$个样本，那么，我们用前述的矩阵表达把这些向量堆叠起来，就有——
\[ W^{[1]}={\begin{bmatrix} w^{[1](1)}_1 & w^{[1](1)}_2 & \cdots & w^{[1](1)}_n\\ w^{[1](2)}_1 & w^{[1](2)}_2 & \cdots& w^{[1](2)}_n\\ \vdots& \vdots & \quad &\vdots\\ w^{[1](m)}_1 & w^{[1](m)}_2 & \cdots & w^{[1](m)}_n \end{bmatrix}}_{m \times n} \]
通过类似的方法，我们就可以逐层完成表示，也就是前向传播过程。相应地，反向传播的过程就是将求导的对象堆叠起来，此处不再赘述。
理论上，两层神经网络可以无限逼近任意连续函数。作者个人并不十分喜欢这句话，在目前的深度学习教材和专著中经常能看见这句话，但对于其原因都未作解释。作者在 Colah的博客中找到了一个反面的验证。实际上就是，面对复杂的非线性分类任务，两层（带一个隐藏层）神经网络可以分类的很好。

Figure 8. 两层神经网络的决策分界
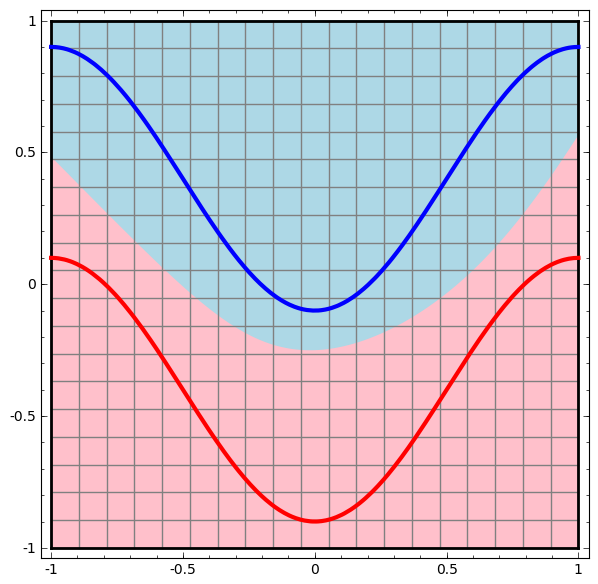
在 Fig.8 中可以看到，这个两层神经网络的决策分界是非常平滑的曲线，而且分类的很好。可是单层网络只能解决线性分类任务，而两层神经网络中的后一层也是线性分类层，应该只能做线性分类任务。为什么两个线性分类任务结合就可以做非线性分类任务？

Figure 9. 空间变换后的决策分界
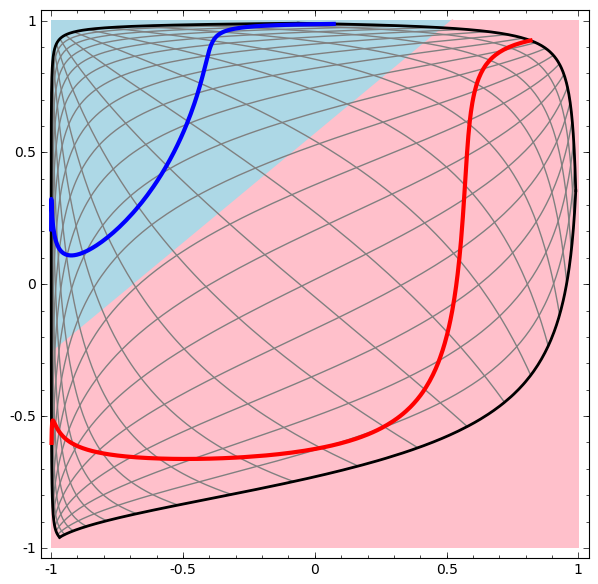
我们把输出层的决策分界单独拿出来看（ Fig.9），输出层的决策分界仍然是直线。关键就是，从输入层到隐藏层时，数据发生了空间变换。也就是说，两层神经网络中，隐藏层对原始的数据进行了一个空间变换，使其可以被线性分类，然后输出层的决策分界划出了一个线性分类分界线，对其进行分类。这样就导出了两层神经网络可以做非线性分类的关键——隐藏层。我们知道，矩阵和向量相乘，本质上就是对向量的坐标空间进行一个变换。因此，隐藏层的参数矩阵的作用就是使得数据的原始坐标空间从线性不可分（ Fig.8 的红蓝区域曲线边界），转换成了线性可分（ Fig.9 的红蓝区域直线边界）。
简而言之，隐藏层干了什么？隐藏层对向量空间进行了空间变换，使得非线性分类问题在变换后的向量空间下变成了线性分类问题。

3.2 深度神经网络

如果我们让网络的层数进一步增加会怎么样？在思路上没有变化，还是前向传播加后向传播的过程，还是要用矩阵来描述问题。此时，我们反而更关注网络本身的问题。

Figure 10.
Fig.10 中的神经网络（神经元）有 $3 \times 1=3$个 $w$参数， $1$个 $b$参数，共有 $3+1=4$个参数。

Figure 11.
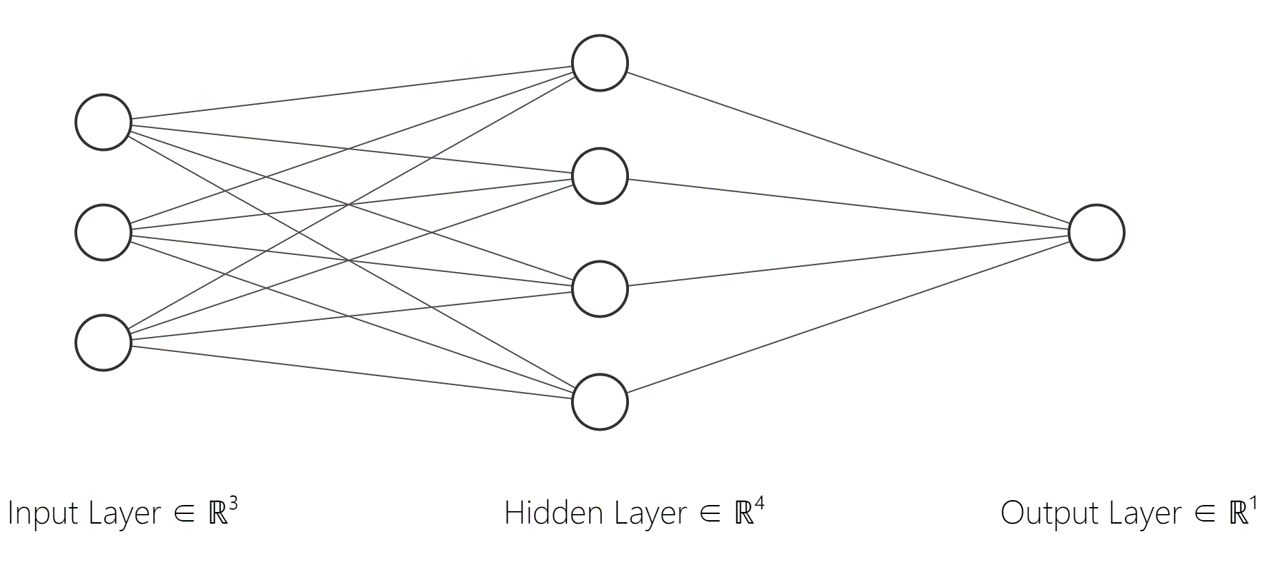
Fig.11 中的神经网络（神经元）有 $3 \times 4+4 \times 1=16$个 $w$参数， $1+1=2$个 $b$参数，共有 $16+2=18$个参数。

Figure 12.
Fig.12 中的神经网络（神经元）有 $8 \times 5+5 \times 5+5 \times 5+ 5 \times 2=100$个 $w$参数， $1+1+1+1=4$个 $b$参数，共有 $100+4=104$个参数。注意在 Fig.12 的网络中，与前面介绍的网络不同，有3个输出。

Figure 13.
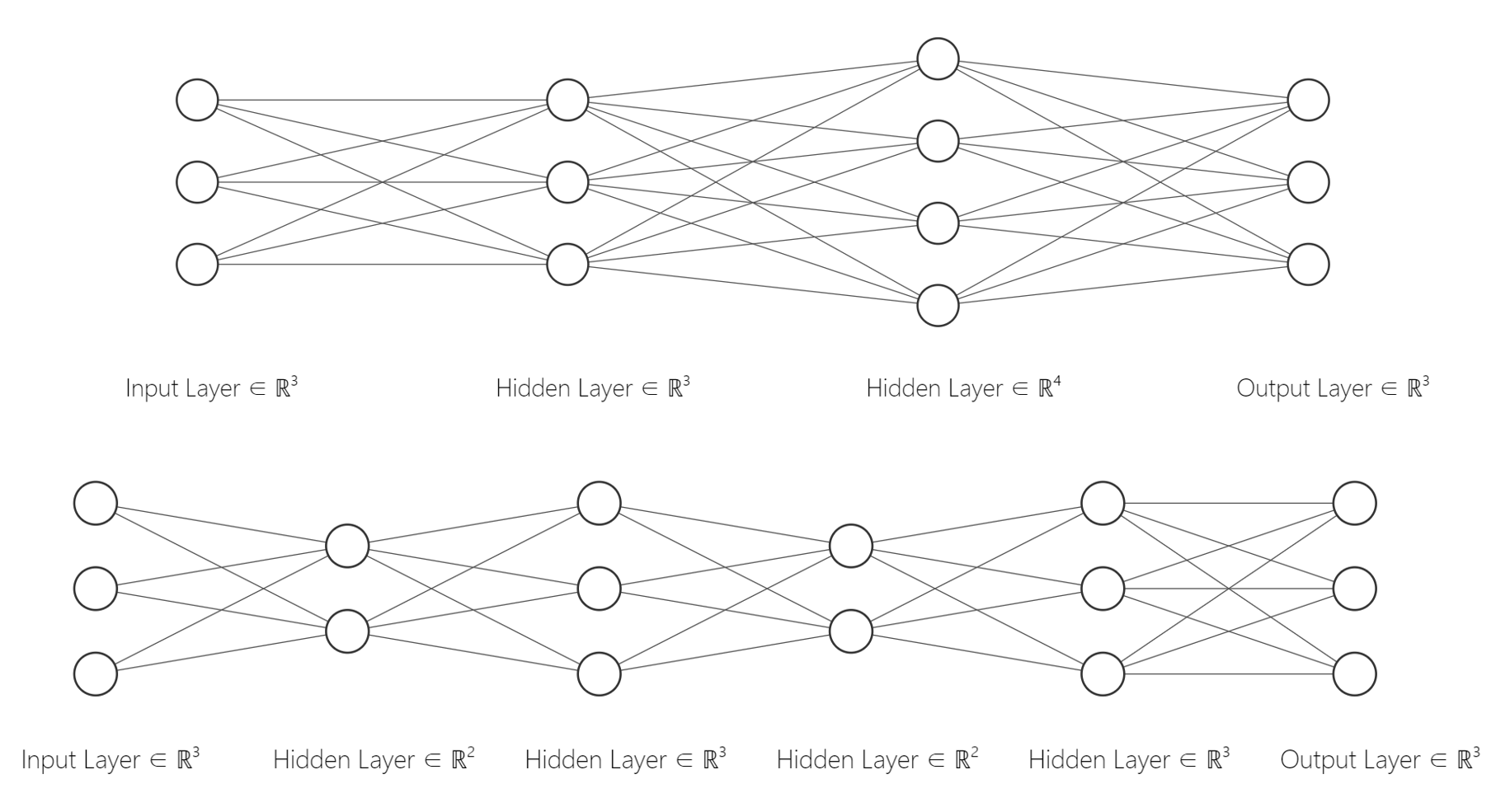
我们讨论参数有什么意义呢? Fig.13 中，上下两个网络，分别有 $33+3=36$个和 $33+5=38$个参数，它们的 $w$参数数量是一致的，但是层数却不同，分别为3层和5层（第0层输入层不计入在内）。这表明，我们可以用相同量的参数，但是更多的层次来构建神经网络，这反映了神经网络的表达能力。 神经网络的表达能力主要由隐层的层数和隐层神经元个数决定。隐藏层的层数就可以看作是神经网络的 深度（Depth），这也就是在神经网络中的机器学习称为“深度”学习（连接主义学派）的原因。 在参数数量一样的情况下，更深的网络往往具有比浅层的网络更好的识别效率。
当然，我们对参数的讨论还没有结束。设计一个神经网络我们要考虑，隐藏层的数量 $\rm \#Layer$，每层的神经元数量 $\rm \#Neuron$，这些量可以视为确定神经网络结构的 超参数（Hyper-parameters）处理。这个问题在卷积神经网络（Convolutionnal Neural Network, CNN）中更为明显。
在Logistic Regression中，神经元的非线性单元使用的激活函数是Sigmoid函数 $\sigma(z)=\frac{1}{1+e^{-z}}$，实际上，目前的神经网络更常用的激活函数还有双曲正切函数（tanh）、线性整流函数/修正线性单元（Rectified Linear Unit, ReLU）和带泄露的修正线性单元（Leaky ReLUs）等。图像如 Fig.14 所示。具体的用法可以参考这里，此处不再说明。

Figure 14. 非线性激活函数

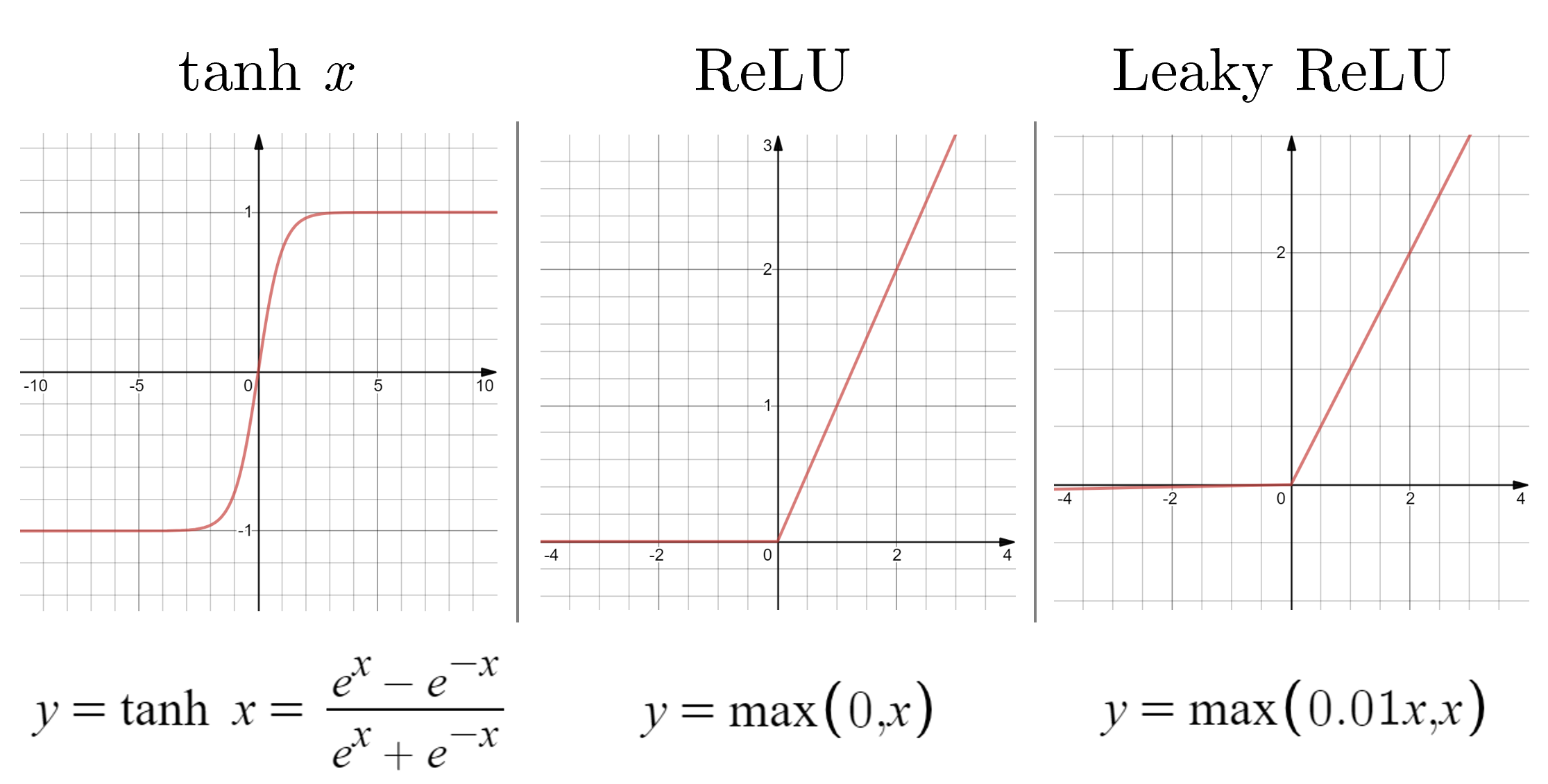
4 总结

生物接受到刺激，$\rm Na^+$离子内流，产生了一个电信号，这个电信号传到神经元胞体时，胞体不知道自己对这个电信号的处理所做为何。但是当前860亿个神经元组织起来，人就产生了智能。这种想法未免失之偏颇，但在作者看来，人工神经网络在本质上并不复杂，“线性运算、非线性激活、梯度下降寻求最优参数给下一次迭代使用”，仅此而已。但是，当神经网络具备一定的规模，神经元达到一定的数量时，这些简单的单元却形成了强大的计算合力。这样量变引起质变的过程，也体现着朴素的唯物辩证法。
作者认为，人工神经网络中要把握的几个“纲”在于——
其一，每个神经元在干什么？前向传播时，它们进行一次加权加偏置的线性运算，再进行一次非线性激活；后向传播时，它们用链式法则求（偏）微分去找最优的参数。然后用这组参数进行下一代（下一个样本）的前向传播。
其二，隐藏层在干什么？隐藏层对向量空间进行了空间变换，使得非线性分类问题在变换后的向量空间下变成了线性分类问题。
其三，一个神经网络是好是坏取决于什么？取决于为解决问题而投入大量样本迭代训练出来的那些最优参数。（这也就是为什么YOLO等模型中.weights文件十分关键的原因。）

Figure 15. 人工神经网络的发展史
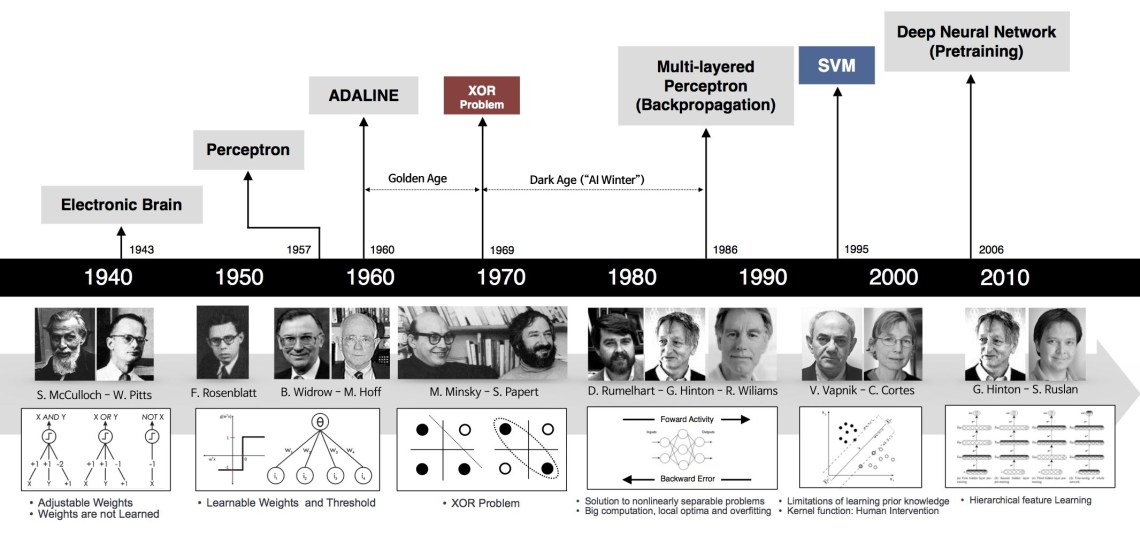
数十年间，人工神经网络起起落落（ Fig.15），彼时的算力远不及此时。而在GPU、并行计算、分布式计算、大数据量支持变得寻常的今天，人工神经网络恰逢其时。不管符号主义学派和连接主义学派相爱相杀争辩到几时，对于面向工程问题的我们来说，“不管白猫黑猫，抓到耗子就是好猫。”

Acknowledgement

在深度神经网络部分，作者参考了“计算机的潜意识”的这篇博文，全文从神经网络的历史角度详细介绍了前向传播网络，一些思想给了作者以很大启发，在此致谢。

作者后记

这篇文档用了3天写完，本来是准备从DNN一直写到CNN、RNN，无奈能力和时间有限，文中也有很多坑没有填上，等待下次修订。
写这篇文档的过程，也是我重新理解经典人工神经网络模型的过程，在思辨中也补上了很多细节。《论语》说，”日知其所亡，月无忘其所能，可谓好学也已矣。“距离这个境界还差得很远，只能鞭策自己积跬步以至千里了。（2020年2月21日子夜）

修订记录

[1] 2020年2月21日发布.

通向深度神经网络之路

A Road to Deep Neural Networks

1 从生物学而来的M-P神经元模型