版权声明:版权所有,尊重原创。转载请注明出处: https://blog.csdn.net/qq_36426650/article/details/84398458
摘要 :深度学习是近年来计算机人工智能领域非常火的研究方向,其相比传统的浅层机器学习而言能够挖掘出更多隐含的特征。深度学习现如今已经广泛的应用与计算机视觉、自然语言处理等领域,因此作为计算机专业人工智能的学习者,学习和研究深度学习是一项必修课。
启发:线性回归
神经网络的结构
神经网络的训练
模型优化
其他经典的神经网络
TensorFlow实现标准神经网络源程序
总结
神经网络的基本计算主要以线性和非线性为主,线性是为了对不同的特征进行相互组合,其主要的运算结果是线性回归问题;非线性处理是为了对模型进行优化,使其能够处理非线性问题,其主要运算以函数形式。
y
^
=
W
T
x
+
b
\hat y = W^Tx+b
y ^ = W T x + b
其中
W
W
W
b
b
b
x
x
x
y
^
\hat y
y ^
D
=
D=
D =
X
X
X
Y
Y
Y
X
=
X=
X =
x
1
,
x
2
,
.
.
.
,
x
n
x_1,x_2,...,x_n
x 1 , x 2 , . . . , x n
Y
=
Y=
Y =
y
1
,
y
2
,
.
.
.
,
y
n
y_1,y_2,...,y_n
y 1 , y 2 , . . . , y n
n
n
n
L
(
y
,
y
^
)
=
1
2
∣
y
−
y
^
∣
2
L(y,\hat y)=\frac{1}{2}|y-\hat y|^2
L ( y , y ^ ) = 2 1 ∣ y − y ^ ∣ 2
则代价函数(所有样本的损失函数的均值)为:
J
(
Y
,
Y
^
)
=
1
2
n
∑
∣
y
−
y
^
∣
2
J(Y,\hat Y)=\frac{1}{2n}\sum|y-\hat y|^2
J ( Y , Y ^ ) = 2 n 1 ∑ ∣ y − y ^ ∣ 2
构造了代价函数后,需要对其进行最优化处理,使得模型的代价尽可能降低。模型的优化方法常用的是梯度下降法(或称最速下降法)。梯度下降法通过对需要优化调整的参数进行调参。线性回归模型中需要调整的参数有权重矩阵
W
W
W
b
b
b
∂
J
∂
W
T
=
∂
J
∂
y
T
⋅
∂
y
T
∂
W
T
=
1
n
⋅
(
y
−
y
^
)
⋅
x
\frac{\partial J}{\partial W^T}=\frac{\partial J}{\partial y^T}·\frac{\partial y^T}{\partial W^T}=\frac{1}{n}·(y-\hat y)·x
∂ W T ∂ J = ∂ y T ∂ J ⋅ ∂ W T ∂ y T = n 1 ⋅ ( y − y ^ ) ⋅ x
∂
J
∂
b
=
∂
J
∂
y
T
⋅
∂
y
T
∂
b
=
1
n
⋅
(
y
−
y
^
)
\frac{\partial J}{\partial b}=\frac{\partial J}{\partial y^T}·\frac{\partial y^T}{\partial b}=\frac{1}{n}·(y-\hat y)
∂ b ∂ J = ∂ y T ∂ J ⋅ ∂ b ∂ y T = n 1 ⋅ ( y − y ^ )
若选择学习率为
α
(
0
<
α
<
1
)
\alpha(0<\alpha<1)
α ( 0 < α < 1 )
W
T
:
W
T
−
α
∂
J
∂
W
T
W^T:W^T-\alpha\frac{\partial J}{\partial W^T}
W T : W T − α ∂ W T ∂ J
b
:
b
−
α
∂
J
∂
b
b:b-\alpha\frac{\partial J}{\partial b}
b : b − α ∂ b ∂ J
通过不断循环调参,直到参数变化非常小的时候(在编程过程中,可以设置一个变量用以判断是否需要下一轮迭代),线性回归模型可以说训练完成。在评估该模型时候,仍然可以使用损失函数来对测试集进行评估,并计算相应的准确率、召回率、F1值等。
深入学习神经网络后会发,神经网络便是若干个线性回归方程的“相互交织”,再通过非线性方程进行“锐化”,因此第一节的线性回归问题是解决神经网络的基础。
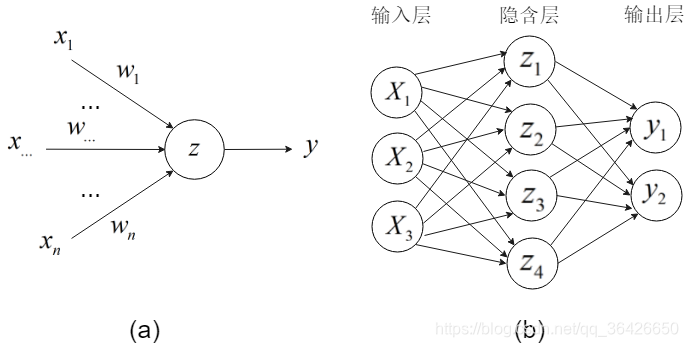
图(a)为一个信息感知机,输入模型的数据为
x
1
,
x
2
,
.
.
.
,
x
n
x_1,x_2,...,x_n
x 1 , x 2 , . . . , x n
w
1
,
w
2
,
.
.
.
,
w
n
w_1,w_2,...,w_n
w 1 , w 2 , . . . , w n
z
=
w
1
x
1
+
w
2
x
2
+
.
.
.
+
w
n
x
n
+
b
z=w_1x_1+w_2x_2+...+w_nx_n+b
z = w 1 x 1 + w 2 x 2 + . . . + w n x n + b
z
=
W
T
+
b
z=W^T+b
z = W T + b
因此,对于单个神经元接受数据部分,是一个典型的线性回归模型。神经元的“激活或抑制反应”主要通过激活函数来完成。常用的激活函数有sigmod、tanh、ReLU、ELU等,这些激活函数都属于非线性函数,函数的输出即为该神经元对外做出的反应,即模型的输出值。以sigmod为例,该神经元的输出为:
a
=
σ
(
W
T
+
b
)
=
1
1
+
e
−
(
W
T
+
b
)
a=\sigma(W^T+b)=\frac{1}{1+e^{-(W^T+b)}}
a = σ ( W T + b ) = 1 + e − ( W T + b ) 1
σ
′
(
z
)
=
σ
(
z
)
(
1
−
σ
(
z
)
)
\sigma'(z)=\sigma(z)(1-\sigma(z))
σ ′ ( z ) = σ ( z ) ( 1 − σ ( z ) )
图(b)是多个神经元相互交织在一起形成网络结构,其称为深度神经网络。深度神经网络常由输入层、隐含层和输出层组成。输入层的神经元个数等于输入样本的特征属性个数,隐含层可以自定个数(通常超过3个),隐含层的数据是不可见的,输出层作为模型的输出部分,神经元个数由需要分类的类标个数决定。
了解了神经网络的结构,需要了解神经网络如何进行训练。神经网络的训练过程分为如下几个步骤:
参数设置:设置模型的参数和超参数,包括权重矩阵、偏向、梯度下降的学习率;
前向传播:根据模型的输入层样本数据,计算每个神经元的接受数据和输出数据,并最终求得模型的输出层数据;
反向传播:选择损失函数并计算代价,选择优化策略(常选择梯度下降法)并进行调参;
模型的评估:根据测试集计算准确率、召回率、F1值等。
1、参数设置 (1)对需要学习的参数进行设置
t
r
a
i
n
=
{
(
X
1
,
Y
1
)
,
(
X
2
,
Y
2
)
,
.
.
.
,
(
X
N
,
Y
N
)
}
train=\{(X_1,Y_1),(X_2,Y_2),...,(X_N,Y_N)\}
t r a i n = { ( X 1 , Y 1 ) , ( X 2 , Y 2 ) , . . . , ( X N , Y N ) }
N
N
N
(
X
i
,
Y
i
)
=
(
x
1
(
i
)
,
x
2
(
i
)
,
x
3
(
i
)
,
y
(
i
)
)
(X_i,Y_i)=(x{_1}{^{(i)}},x{_2}{^{(i)}},x{_3}{^{(i)}},y^{(i)})
( X i , Y i ) = ( x 1 ( i ) , x 2 ( i ) , x 3 ( i ) , y ( i ) )
Y
i
∈
{
0
,
1
}
Y_i \in\mathbb \{0,1\}
Y i ∈ { 0 , 1 }
W
[
1
]
=
[
w
11
[
1
]
w
21
[
1
]
w
31
[
1
]
w
12
[
1
]
w
22
[
1
]
w
32
[
1
]
w
13
[
1
]
w
23
[
1
]
w
33
[
1
]
w
14
[
1
]
w
24
[
1
]
w
34
[
1
]
]
W{^{[1]}}= \begin{bmatrix} w{_{11}}{^{[1]}} & w{_{21}}{^{[1]}} & w{_{31}}{^{[1]}} \\ w{_{12}}{^{[1]}} & w{_{22}}{^{[1]}} & w{_{32}}{^{[1]}} \\ w{_{13}}{^{[1]}} & w{_{23}}{^{[1]}} & w{_{33}}{^{[1]}} \\ w{_{14}}{^{[1]}} & w{_{24}}{^{[1]}} & w{_{34}}{^{[1]}} \\ \end{bmatrix}
W [ 1 ] = ⎣ ⎢ ⎢ ⎡ w 1 1 [ 1 ] w 1 2 [ 1 ] w 1 3 [ 1 ] w 1 4 [ 1 ] w 2 1 [ 1 ] w 2 2 [ 1 ] w 2 3 [ 1 ] w 2 4 [ 1 ] w 3 1 [ 1 ] w 3 2 [ 1 ] w 3 3 [ 1 ] w 3 4 [ 1 ] ⎦ ⎥ ⎥ ⎤
W
[
1
]
W{^{[1]}}
W [ 1 ]
W
[
2
]
W{^{[2]}}
W [ 2 ]
W
[
2
]
=
[
w
11
[
2
]
w
21
[
2
]
w
31
[
2
]
w
41
[
2
]
w
12
[
2
]
w
22
[
2
]
w
32
[
2
]
w
42
[
2
]
]
W{^{[2]}}= \begin{bmatrix} w{_{11}}{^{[2]}} & w{_{21}}{^{[2]}} & w{_{31}}{^{[2]}} & w{_{41}}{^{[2]}} \\ w{_{12}}{^{[2]}} & w{_{22}}{^{[2]}} & w{_{32}}{^{[2]}} & w{_{42}}{^{[2]}} \\ \end{bmatrix}
W [ 2 ] = [ w 1 1 [ 2 ] w 1 2 [ 2 ] w 2 1 [ 2 ] w 2 2 [ 2 ] w 3 1 [ 2 ] w 3 2 [ 2 ] w 4 1 [ 2 ] w 4 2 [ 2 ] ]
W
[
2
]
W{^{[2]}}
W [ 2 ]
b
[
1
]
=
[
b
1
[
1
]
b
2
[
1
]
b
3
[
1
]
b
4
[
1
]
]
T
b{^{[1]}}=\begin{bmatrix}b{_1}{^{[1]}} & b{_2}{^{[1]}} & b{_3}{^{[1]}} & b{_4}{^{[1]}}\end{bmatrix}^T
b [ 1 ] = [ b 1 [ 1 ] b 2 [ 1 ] b 3 [ 1 ] b 4 [ 1 ] ] T
b
[
2
]
=
[
b
1
[
2
]
b
2
[
2
]
b
3
[
2
]
b
4
[
2
]
]
T
b{^{[2]}}=\begin{bmatrix}b{_1}{^{[2]}} & b{_2}{^{[2]}} & b{_3}{^{[2]}} & b{_4}{^{[2]}}\end{bmatrix}^T
b [ 2 ] = [ b 1 [ 2 ] b 2 [ 2 ] b 3 [ 2 ] b 4 [ 2 ] ] T
(2)对超参数进行设置
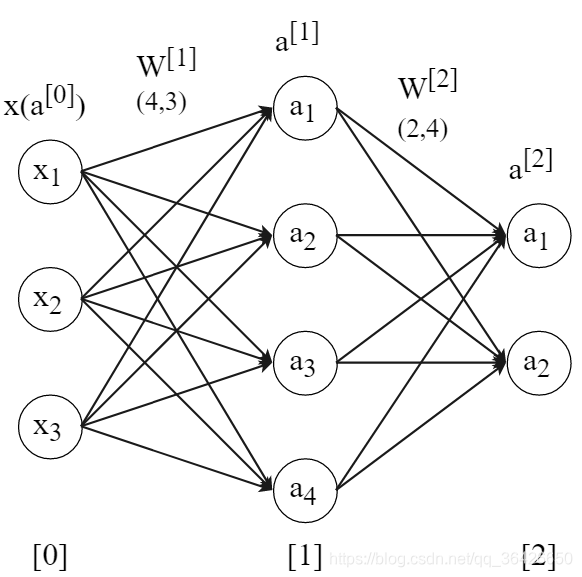
2、前向传播 为了详细表达运算,先以单个样本进行前向传播的详细推导
z
1
[
1
]
=
w
11
[
1
]
x
1
+
w
21
[
2
]
x
2
+
w
31
[
1
]
x
3
+
b
1
[
1
]
z{{_1}{^{[1]}}}=w{{_{11}}{^{[1]}}}x_1+w{{_{21}}{^{[2]}}}x_2+w{{_{31}}{^{[1]}}}x_3+b{_1}{^{[1]}}
z 1 [ 1 ] = w 1 1 [ 1 ] x 1 + w 2 1 [ 2 ] x 2 + w 3 1 [ 1 ] x 3 + b 1 [ 1 ]
z
2
[
1
]
=
w
12
[
1
]
x
1
+
w
22
[
2
]
x
2
+
w
32
[
1
]
x
3
+
b
2
[
1
]
z{{_2}{^{[1]}}}=w{{_{12}}{^{[1]}}}x_1+w{{_{22}}{^{[2]}}}x_2+w{{_{32}}{^{[1]}}}x_3+b{_2}{^{[1]}}
z 2 [ 1 ] = w 1 2 [ 1 ] x 1 + w 2 2 [ 2 ] x 2 + w 3 2 [ 1 ] x 3 + b 2 [ 1 ]
z
3
[
1
]
=
w
13
[
1
]
x
1
+
w
23
[
2
]
x
2
+
w
33
[
1
]
x
3
+
b
3
[
1
]
z{{_3}{^{[1]}}}=w{{_{13}}{^{[1]}}}x_1+w{{_{23}}{^{[2]}}}x_2+w{{_{33}}{^{[1]}}}x_3+b{_3}{^{[1]}}
z 3 [ 1 ] = w 1 3 [ 1 ] x 1 + w 2 3 [ 2 ] x 2 + w 3 3 [ 1 ] x 3 + b 3 [ 1 ]
z
4
[
1
]
=
w
14
[
1
]
x
1
+
w
24
[
2
]
x
2
+
w
34
[
1
]
x
3
+
b
4
[
1
]
z{{_4}{^{[1]}}}=w{{_{14}}{^{[1]}}}x_1+w{{_{24}}{^{[2]}}}x_2+w{{_{34}}{^{[1]}}}x_3+b{_4}{^{[1]}}
z 4 [ 1 ] = w 1 4 [ 1 ] x 1 + w 2 4 [ 2 ] x 2 + w 3 4 [ 1 ] x 3 + b 4 [ 1 ]
z
[
1
]
=
W
[
1
]
x
+
b
[
1
]
=
[
w
11
[
1
]
w
21
[
1
]
w
31
[
1
]
w
12
[
1
]
w
22
[
1
]
w
32
[
1
]
w
13
[
1
]
w
23
[
1
]
w
33
[
1
]
w
14
[
1
]
w
24
[
1
]
w
34
[
1
]
]
[
x
1
x
2
x
3
x
4
]
+
[
b
1
[
1
]
b
2
[
1
]
b
3
[
1
]
b
4
[
1
]
]
z{^{[1]}}=W{^{[1]}}x+b{^{[1]}}= \begin{bmatrix} w{_{11}}{^{[1]}} & w{_{21}}{^{[1]}} & w{_{31}}{^{[1]}} \\ w{_{12}}{^{[1]}} & w{_{22}}{^{[1]}} & w{_{32}}{^{[1]}} \\ w{_{13}}{^{[1]}} & w{_{23}}{^{[1]}} & w{_{33}}{^{[1]}} \\ w{_{14}}{^{[1]}} & w{_{24}}{^{[1]}} & w{_{34}}{^{[1]}} \\ \end{bmatrix} \begin{bmatrix} x{_1} \\ x{_2} \\ x{_3} \\ x{_4} \\ \end{bmatrix}+ \begin{bmatrix} b{_{1}}{^{[1]}} \\ b{_{2}}{^{[1]}} \\ b{_{3}}{^{[1]}} \\ b{_{4}}{^{[1]}} \\ \end{bmatrix}
z [ 1 ] = W [ 1 ] x + b [ 1 ] = ⎣ ⎢ ⎢ ⎡ w 1 1 [ 1 ] w 1 2 [ 1 ] w 1 3 [ 1 ] w 1 4 [ 1 ] w 2 1 [ 1 ] w 2 2 [ 1 ] w 2 3 [ 1 ] w 2 4 [ 1 ] w 3 1 [ 1 ] w 3 2 [ 1 ] w 3 3 [ 1 ] w 3 4 [ 1 ] ⎦ ⎥ ⎥ ⎤ ⎣ ⎢ ⎢ ⎡ x 1 x 2 x 3 x 4 ⎦ ⎥ ⎥ ⎤ + ⎣ ⎢ ⎢ ⎡ b 1 [ 1 ] b 2 [ 1 ] b 3 [ 1 ] b 4 [ 1 ] ⎦ ⎥ ⎥ ⎤
z
[
1
]
z{^{[1]}}
z [ 1 ]
a
[
1
]
=
σ
(
z
[
1
]
)
a{^{[1]}}=\sigma(z{^{[1]}})
a [ 1 ] = σ ( z [ 1 ] )
其次,隐含层将数据传输给输出层,输入数据此时为
a
[
1
]
a{^{[1]}}
a [ 1 ]
z
1
[
2
]
=
w
11
[
2
]
a
1
[
1
]
+
w
21
[
2
]
a
2
[
1
]
+
w
31
[
2
]
a
3
[
1
]
+
w
41
[
2
]
a
4
[
1
]
+
b
1
[
2
]
z{{_1}{^{[2]}}}=w{{_{11}}{^{[2]}}}a{_{1}}{^{[1]}}+w{{_{21}}{^{[2]}}}a{_{2}}{^{[1]}}+w{{_{31}}{^{[2]}}}a{_{3}}{^{[1]}}+w{{_{41}}{^{[2]}}}a{_{4}}{^{[1]}}+b{_1}{^{[2]}}
z 1 [ 2 ] = w 1 1 [ 2 ] a 1 [ 1 ] + w 2 1 [ 2 ] a 2 [ 1 ] + w 3 1 [ 2 ] a 3 [ 1 ] + w 4 1 [ 2 ] a 4 [ 1 ] + b 1 [ 2 ]
z
2
[
2
]
=
w
12
[
2
]
a
1
[
1
]
+
w
22
[
2
]
a
2
[
1
]
+
w
32
[
2
]
a
3
[
1
]
+
w
42
[
2
]
a
4
[
1
]
+
b
2
[
2
]
z{{_2}{^{[2]}}}=w{{_{12}}{^{[2]}}}a{_{1}}{^{[1]}}+w{{_{22}}{^{[2]}}}a{_{2}}{^{[1]}}+w{{_{32}}{^{[2]}}}a{_{3}}{^{[1]}}+w{{_{42}}{^{[2]}}}a{_{4}}{^{[1]}}+b{_2}{^{[2]}}
z 2 [ 2 ] = w 1 2 [ 2 ] a 1 [ 1 ] + w 2 2 [ 2 ] a 2 [ 1 ] + w 3 2 [ 2 ] a 3 [ 1 ] + w 4 2 [ 2 ] a 4 [ 1 ] + b 2 [ 2 ]
z
[
2
]
=
W
[
2
]
a
[
1
]
+
b
[
2
]
=
[
w
11
[
2
]
w
21
[
2
]
w
31
[
2
]
w
41
[
2
]
w
12
[
2
]
w
22
[
2
]
w
32
[
2
]
w
42
[
2
]
]
[
a
1
[
2
]
a
2
[
2
]
a
3
[
2
]
a
4
[
2
]
]
+
[
b
1
[
2
]
b
2
[
2
]
b
3
[
2
]
b
4
[
2
]
]
z{^{[2]}}=W{^{[2]}}a{^{[1]}}+b{^{[2]}}= \begin{bmatrix} w{_{11}}{^{[2]}} & w{_{21}}{^{[2]}} & w{_{31}}{^{[2]}} & w{_{41}}{^{[2]}} \\ w{_{12}}{^{[2]}} & w{_{22}}{^{[2]}} & w{_{32}}{^{[2]}} & w{_{42}}{^{[2]}} \\ \end{bmatrix} \begin{bmatrix} a{_{1}}{^{[2]}} \\ a{_{2}}{^{[2]}} \\ a{_{3}}{^{[2]}} \\ a{_{4}}{^{[2]}} \\ \end{bmatrix}+ \begin{bmatrix} b{_{1}}{^{[2]}} \\ b{_{2}}{^{[2]}} \\ b{_{3}}{^{[2]}} \\ b{_{4}}{^{[2]}} \\ \end{bmatrix}
z [ 2 ] = W [ 2 ] a [ 1 ] + b [ 2 ] = [ w 1 1 [ 2 ] w 1 2 [ 2 ] w 2 1 [ 2 ] w 2 2 [ 2 ] w 3 1 [ 2 ] w 3 2 [ 2 ] w 4 1 [ 2 ] w 4 2 [ 2 ] ] ⎣ ⎢ ⎢ ⎡ a 1 [ 2 ] a 2 [ 2 ] a 3 [ 2 ] a 4 [ 2 ] ⎦ ⎥ ⎥ ⎤ + ⎣ ⎢ ⎢ ⎡ b 1 [ 2 ] b 2 [ 2 ] b 3 [ 2 ] b 4 [ 2 ] ⎦ ⎥ ⎥ ⎤
最后,获得的输出喂给sigmoid函数(通常最后都喂给softmax函数,这里为了方便反向传播求导,仍然使用sigmoid函数),
y
^
=
a
[
2
]
=
σ
(
z
[
2
]
)
\hat y=a{^{[2]}}=\sigma(z{^{[2]}})
y ^ = a [ 2 ] = σ ( z [ 2 ] )
因为该神经网络的输出层一共两个结点,因此对于单个样本,输出格式为[*,*]。
(2)对于多个样本 ,可以采用显示for循环方式按如上方式运算,但这样有明显两个缺点:一个是通过for循环显示进行循环非常耗时,第二是当数据量非常庞大时候对训练参数非常不利,因此对于多样本进行前向传播时,选择向量运算。假设样本集为
X
X
X
n
n
n
X
X
X
n
n
n
Z
[
1
]
=
W
[
1
]
X
+
b
[
1
]
Z^{[1]}=W^{[1]}X+b^{[1]}
Z [ 1 ] = W [ 1 ] X + b [ 1 ]
A
[
1
]
=
σ
(
Z
[
1
]
)
A^{[1]}=\sigma(Z{^{[1]}})
A [ 1 ] = σ ( Z [ 1 ] )
n
n
n
Z
[
2
]
=
W
[
2
]
A
[
1
]
+
b
[
2
]
Z^{[2]}=W^{[2]}A^{[1]}+b^{[2]}
Z [ 2 ] = W [ 2 ] A [ 1 ] + b [ 2 ]
A
[
2
]
=
σ
(
Z
[
2
]
)
A^{[2]}=\sigma(Z{^{[2]}})
A [ 2 ] = σ ( Z [ 2 ] )
n
n
n
3、反向传播
神经网络的训练关键就是训练它的权重矩阵和偏向,反向传播就是在不断地根据当前参数对样本产生的误差进行调整,以保证该误差尽可能小。反向传播时理解神经网络算法的核心。偏导数的链式法则 实现反向传播,选择的损失函数是交差信息熵。为了详细推导梯度下降的反向传播,同样先以单个样本为例:单样本反向传播 :根据单样本的前向传播推导,得到最终的输出值:
y
^
=
a
[
2
]
\hat y=a^{[2]}
y ^ = a [ 2 ]
损失函数交差信息熵表达式是:
L
(
y
,
y
^
)
=
L
(
y
,
a
[
2
]
)
=
−
[
y
l
n
a
[
2
]
+
(
1
−
y
)
l
n
(
1
−
a
[
2
]
)
)
]
L(y,\hat y)=L(y,a^{[2]})=-[ylna^{[2]}+(1-y)ln(1-a^{[2])})]
L ( y , y ^ ) = L ( y , a [ 2 ] ) = − [ y l n a [ 2 ] + ( 1 − y ) l n ( 1 − a [ 2 ] ) ) ]
因此可求出
L
L
L
a
[
2
]
a^{[2]}
a [ 2 ]
∂
L
∂
a
[
2
]
=
−
y
a
[
2
]
+
1
−
y
1
−
a
[
2
]
\frac{\partial L}{\partial a^{[2]}} = -\frac{y}{a^{[2]}}+\frac{1-y}{1-a^{[2]}}
∂ a [ 2 ] ∂ L = − a [ 2 ] y + 1 − a [ 2 ] 1 − y
由
y
^
=
a
[
2
]
=
σ
(
z
[
2
]
)
\hat y=a{^{[2]}}=\sigma(z{^{[2]}})
y ^ = a [ 2 ] = σ ( z [ 2 ] )
L
L
L
z
[
2
]
z^{[2]}
z [ 2 ]
∂
L
∂
z
[
2
]
=
∂
L
∂
a
[
2
]
∂
a
[
2
]
∂
z
[
2
]
=
(
−
y
a
[
2
]
+
1
−
y
1
−
a
[
2
]
)
σ
(
z
[
2
]
)
(
1
−
σ
(
z
[
2
]
)
)
\frac{\partial L}{\partial z^{[2]}} = \frac{\partial L}{\partial a^{[2]}}\frac{\partial a^{[2]}}{\partial z^{[2]}} = (-\frac{y}{a^{[2]}}+\frac{1-y}{1-a^{[2]}})\sigma(z^{[2]})(1-\sigma(z^{[2]}))
∂ z [ 2 ] ∂ L = ∂ a [ 2 ] ∂ L ∂ z [ 2 ] ∂ a [ 2 ] = ( − a [ 2 ] y + 1 − a [ 2 ] 1 − y ) σ ( z [ 2 ] ) ( 1 − σ ( z [ 2 ] ) )
=
(
−
y
a
[
2
]
+
1
−
y
1
−
a
[
2
]
)
a
[
2
]
(
1
−
a
[
2
]
)
=(-\frac{y}{a{^{[2]}}}+\frac{1-y}{1-a{^{[2]}}})a{^{[2]}}(1-a{^{[2]}})
= ( − a [ 2 ] y + 1 − a [ 2 ] 1 − y ) a [ 2 ] ( 1 − a [ 2 ] )
=
y
(
a
[
2
]
−
1
)
+
(
1
−
y
)
a
[
2
]
=
a
[
2
]
−
y
=y(a{^{[2]}}-1)+(1-y)a{^{[2]}}=a{^{[2]}}-y
= y ( a [ 2 ] − 1 ) + ( 1 − y ) a [ 2 ] = a [ 2 ] − y
下面将要对权重矩阵和偏向进行求导,计算之前先进行必要的分析:隐层的神经元与输出层神经元相连的边都是唯一的,因此对于每一条边可通过链式法则求偏导:
z
1
[
2
]
=
w
11
[
2
]
a
1
[
1
]
+
.
.
.
+
b
1
[
2
]
z{{_1}{^{[2]}}}=w{{_{11}}{^{[2]}}}a{_{1}}{^{[1]}}+...+b{_1}{^{[2]}}
z 1 [ 2 ] = w 1 1 [ 2 ] a 1 [ 1 ] + . . . + b 1 [ 2 ]
z
2
[
2
]
=
w
12
[
2
]
a
1
[
1
]
+
.
.
.
+
b
2
[
2
]
z{{_2}{^{[2]}}}=w{{_{12}}{^{[2]}}}a{_{1}}{^{[1]}}+...+b{_2}{^{[2]}}
z 2 [ 2 ] = w 1 2 [ 2 ] a 1 [ 1 ] + . . . + b 2 [ 2 ]
因此对于权重
W
11
[
2
]
W{_{11}}{^{[2]}}
W 1 1 [ 2 ]
∂
L
∂
W
11
[
2
]
=
∂
L
∂
z
1
[
2
]
∂
z
1
[
2
]
∂
W
11
[
2
]
=
(
a
1
[
2
]
−
y
)
a
1
[
1
]
T
\frac{\partial L}{\partial W{_{11}}{^{[2]}}} = \frac{\partial L}{\partial z{_{1}}^{[2]}}\frac{\partial z{_{1}}^{[2]}}{\partial W{_{11}}{^{[2]}}} = (a{_{1}}{^{[2]}}-y)a{_{1}}{^{[1]T}}
∂ W 1 1 [ 2 ] ∂ L = ∂ z 1 [ 2 ] ∂ L ∂ W 1 1 [ 2 ] ∂ z 1 [ 2 ] = ( a 1 [ 2 ] − y ) a 1 [ 1 ] T
对于权重
W
12
[
2
]
W{_{12}}{^{[2]}}
W 1 2 [ 2 ]
∂
L
∂
W
12
[
2
]
=
∂
L
∂
z
2
[
2
]
∂
z
2
[
2
]
∂
W
12
[
2
]
=
(
a
2
[
2
]
−
y
)
a
1
[
1
]
T
\frac{\partial L}{\partial W{_{12}}{^{[2]}}} = \frac{\partial L}{\partial z{_{2}}^{[2]}}\frac{\partial z{_{2}}^{[2]}}{\partial W{_{12}}{^{[2]}}} = (a{_{2}}{^{[2]}}-y)a{_{1}}{^{[1]T}}
∂ W 1 2 [ 2 ] ∂ L = ∂ z 2 [ 2 ] ∂ L ∂ W 1 2 [ 2 ] ∂ z 2 [ 2 ] = ( a 2 [ 2 ] − y ) a 1 [ 1 ] T
因此可以归纳出一个对于边
W
i
j
[
2
]
W{_{ij}}{^{[2]}}
W i j [ 2 ]
∂
L
∂
W
i
j
[
2
]
=
∂
L
∂
z
j
[
2
]
∂
z
j
[
2
]
∂
W
i
j
[
2
]
=
(
a
j
[
2
]
−
y
)
a
i
[
1
]
T
\frac{\partial L}{\partial W{_{ij}}{^{[2]}}} = \frac{\partial L}{\partial z{_{j}}^{[2]}}\frac{\partial z{_{j}}^{[2]}}{\partial W{_{ij}}{^{[2]}}} = (a{_{j}}{^{[2]}}-y)a{_{i}}{^{[1]T}}
∂ W i j [ 2 ] ∂ L = ∂ z j [ 2 ] ∂ L ∂ W i j [ 2 ] ∂ z j [ 2 ] = ( a j [ 2 ] − y ) a i [ 1 ] T
对于输出层的偏向,以输出层第一个神经元为例,列出涉及到的前向传播一个式子:
z
1
[
2
]
=
w
11
[
2
]
a
1
[
1
]
+
w
21
[
2
]
a
2
[
1
]
+
w
31
[
2
]
a
3
[
1
]
+
w
41
[
2
]
a
4
[
1
]
+
b
1
[
2
]
z{{_1}{^{[2]}}}=w{{_{11}}{^{[2]}}}a{_{1}}{^{[1]}}+w{{_{21}}{^{[2]}}}a{_{2}}{^{[1]}}+w{{_{31}}{^{[2]}}}a{_{3}}{^{[1]}}+w{{_{41}}{^{[2]}}}a{_{4}}{^{[1]}}+b{_1}{^{[2]}}
z 1 [ 2 ] = w 1 1 [ 2 ] a 1 [ 1 ] + w 2 1 [ 2 ] a 2 [ 1 ] + w 3 1 [ 2 ] a 3 [ 1 ] + w 4 1 [ 2 ] a 4 [ 1 ] + b 1 [ 2 ]
,由前向传播式子可以很简单的求出导数为:
∂
L
∂
b
1
[
2
]
=
∂
L
∂
z
1
[
2
]
∂
z
1
[
2
]
∂
b
1
[
2
]
=
a
1
[
2
]
−
y
\frac{\partial L}{\partial b{_{1}}{^{[2]}}} = \frac{\partial L}{\partial z{_{1}}^{[2]}}\frac{\partial z{_{1}}^{[2]}}{\partial b{_{1}}{^{[2]}}} = a{_{1}}{^{[2]}}-y
∂ b 1 [ 2 ] ∂ L = ∂ z 1 [ 2 ] ∂ L ∂ b 1 [ 2 ] ∂ z 1 [ 2 ] = a 1 [ 2 ] − y
∂
L
∂
b
2
[
2
]
=
∂
L
∂
z
2
[
2
]
∂
z
2
[
2
]
∂
b
2
[
2
]
=
a
2
[
2
]
−
y
\frac{\partial L}{\partial b{_{2}}{^{[2]}}} = \frac{\partial L}{\partial z{_{2}}^{[2]}}\frac{\partial z{_{2}}^{[2]}}{\partial b{_{2}}{^{[2]}}} = a{_{2}}{^{[2]}}-y
∂ b 2 [ 2 ] ∂ L = ∂ z 2 [ 2 ] ∂ L ∂ b 2 [ 2 ] ∂ z 2 [ 2 ] = a 2 [ 2 ] − y
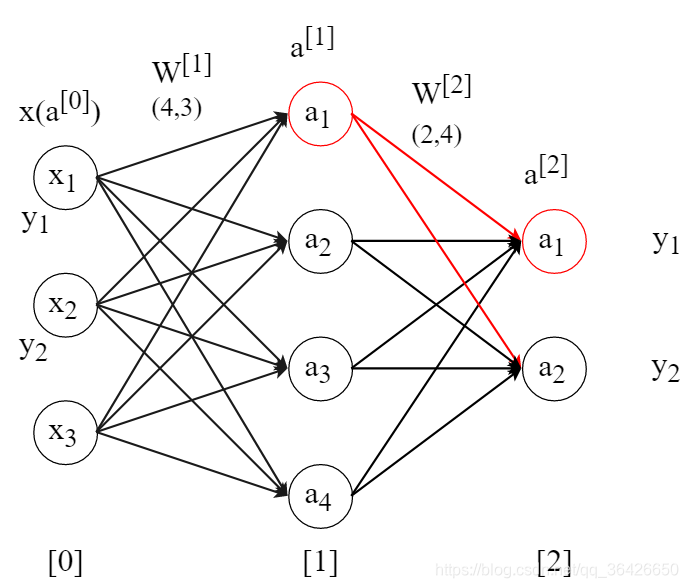
对于隐含层的求导较为复杂,如下图,对于隐含层的某一个神经元,其将收到所有输出层神经元的反向传播,因此对于隐含层的每一个神经元的输出值求导需要分别对所有输出层进行偏导求和。
涉及到的前向传播式子还是这个:
z
1
[
2
]
=
w
11
[
2
]
a
1
[
1
]
+
.
.
.
+
b
1
[
2
]
z{{_1}{^{[2]}}}=w{{_{11}}{^{[2]}}}a{_{1}}{^{[1]}}+...+b{_1}{^{[2]}}
z 1 [ 2 ] = w 1 1 [ 2 ] a 1 [ 1 ] + . . . + b 1 [ 2 ]
z
2
[
2
]
=
w
12
[
2
]
a
1
[
1
]
+
.
.
.
+
b
2
[
2
]
z{{_2}{^{[2]}}}=w{{_{12}}{^{[2]}}}a{_{1}}{^{[1]}}+...+b{_2}{^{[2]}}
z 2 [ 2 ] = w 1 2 [ 2 ] a 1 [ 1 ] + . . . + b 2 [ 2 ]
因此可求出
L
L
L
a
1
[
1
]
a{_1}{^{[1]}}
a 1 [ 1 ]
∂
L
∂
a
1
[
1
]
=
∂
L
∂
z
1
[
2
]
∂
z
1
[
2
]
∂
a
1
[
1
]
+
∂
L
∂
z
2
[
2
]
∂
z
2
[
2
]
∂
a
1
[
1
]
\frac{\partial L}{\partial a{_1}{^{[1]}}} = \frac{\partial L}{\partial z{_1}{^{[2]}}}\frac{\partial z{_1}{^{[2]}}}{\partial a{_1}{^{[1]}}} +\frac{\partial L}{\partial z{_2}{^{[2]}}}\frac{\partial z{_2}{^{[2]}}}{\partial a{_1}{^{[1]}}}
∂ a 1 [ 1 ] ∂ L = ∂ z 1 [ 2 ] ∂ L ∂ a 1 [ 1 ] ∂ z 1 [ 2 ] + ∂ z 2 [ 2 ] ∂ L ∂ a 1 [ 1 ] ∂ z 2 [ 2 ]
=
(
a
1
[
2
]
−
y
)
w
11
[
2
]
+
(
a
2
[
2
]
−
y
)
w
12
[
2
]
=(a{_{1}}{^{[2]}}-y)w{{_{11}}{^{[2]}}}+(a{_{2}}{^{[2]}}-y)w{{_{12}}{^{[2]}}}
= ( a 1 [ 2 ] − y ) w 1 1 [ 2 ] + ( a 2 [ 2 ] − y ) w 1 2 [ 2 ]
由此可以列出另三个:
∂
L
∂
a
2
[
1
]
=
∂
L
∂
z
1
[
2
]
∂
z
1
[
2
]
∂
a
2
[
1
]
+
∂
L
∂
z
2
[
2
]
∂
z
2
[
2
]
∂
a
2
[
1
]
\frac{\partial L}{\partial a{_2}{^{[1]}}} = \frac{\partial L}{\partial z{_1}{^{[2]}}}\frac{\partial z{_1}{^{[2]}}}{\partial a{_2}{^{[1]}}} +\frac{\partial L}{\partial z{_2}{^{[2]}}}\frac{\partial z{_2}{^{[2]}}}{\partial a{_2}{^{[1]}}}
∂ a 2 [ 1 ] ∂ L = ∂ z 1 [ 2 ] ∂ L ∂ a 2 [ 1 ] ∂ z 1 [ 2 ] + ∂ z 2 [ 2 ] ∂ L ∂ a 2 [ 1 ] ∂ z 2 [ 2 ]
=
(
a
1
[
2
]
−
y
)
w
21
[
2
]
+
(
a
2
[
2
]
−
y
)
w
22
[
2
]
=(a{_{1}}{^{[2]}}-y)w{{_{21}}{^{[2]}}}+(a{_{2}}{^{[2]}}-y)w{{_{22}}{^{[2]}}}
= ( a 1 [ 2 ] − y ) w 2 1 [ 2 ] + ( a 2 [ 2 ] − y ) w 2 2 [ 2 ]
∂
L
∂
a
3
[
1
]
=
∂
L
∂
z
1
[
2
]
∂
z
1
[
2
]
∂
a
3
[
1
]
+
∂
L
∂
z
2
[
2
]
∂
z
2
[
2
]
∂
a
3
[
1
]
\frac{\partial L}{\partial a{_3}{^{[1]}}} = \frac{\partial L}{\partial z{_1}{^{[2]}}}\frac{\partial z{_1}{^{[2]}}}{\partial a{_3}{^{[1]}}} +\frac{\partial L}{\partial z{_2}{^{[2]}}}\frac{\partial z{_2}{^{[2]}}}{\partial a{_3}{^{[1]}}}
∂ a 3 [ 1 ] ∂ L = ∂ z 1 [ 2 ] ∂ L ∂ a 3 [ 1 ] ∂ z 1 [ 2 ] + ∂ z 2 [ 2 ] ∂ L ∂ a 3 [ 1 ] ∂ z 2 [ 2 ]
=
(
a
1
[
2
]
−
y
)
w
31
[
2
]
+
(
a
2
[
2
]
−
y
)
w
32
[
2
]
=(a{_{1}}{^{[2]}}-y)w{{_{31}}{^{[2]}}}+(a{_{2}}{^{[2]}}-y)w{{_{32}}{^{[2]}}}
= ( a 1 [ 2 ] − y ) w 3 1 [ 2 ] + ( a 2 [ 2 ] − y ) w 3 2 [ 2 ]
∂
L
∂
a
4
[
1
]
=
∂
L
∂
z
1
[
2
]
∂
z
1
[
2
]
∂
a
4
[
1
]
+
∂
L
∂
z
2
[
2
]
∂
z
2
[
2
]
∂
a
4
[
1
]
\frac{\partial L}{\partial a{_4}{^{[1]}}} = \frac{\partial L}{\partial z{_1}{^{[2]}}}\frac{\partial z{_1}{^{[2]}}}{\partial a{_4}{^{[1]}}} +\frac{\partial L}{\partial z{_2}{^{[2]}}}\frac{\partial z{_2}{^{[2]}}}{\partial a{_4}{^{[1]}}}
∂ a 4 [ 1 ] ∂ L = ∂ z 1 [ 2 ] ∂ L ∂ a 4 [ 1 ] ∂ z 1 [ 2 ] + ∂ z 2 [ 2 ] ∂ L ∂ a 4 [ 1 ] ∂ z 2 [ 2 ]
=
(
a
1
[
2
]
−
y
)
w
41
[
2
]
+
(
a
2
[
2
]
−
y
)
w
42
[
2
]
=(a{_{1}}{^{[2]}}-y)w{{_{41}}{^{[2]}}}+(a{_{2}}{^{[2]}}-y)w{{_{42}}{^{[2]}}}
= ( a 1 [ 2 ] − y ) w 4 1 [ 2 ] + ( a 2 [ 2 ] − y ) w 4 2 [ 2 ]
合并起来可以以矩阵形式呈现:
∂
L
∂
a
[
1
]
=
∂
L
∂
z
1
[
2
]
∂
z
1
[
2
]
∂
a
[
1
]
+
∂
L
∂
z
2
[
2
]
∂
z
2
[
2
]
∂
a
[
1
]
=
[
w
11
[
2
]
w
12
[
2
]
w
21
[
2
]
w
22
[
2
]
w
31
[
2
]
w
32
[
2
]
w
41
[
2
]
w
42
[
2
]
]
[
a
1
[
2
]
−
y
a
2
[
2
]
−
y
]
=
w
[
2
]
T
a
[
2
]
\frac{\partial L}{\partial a{^{[1]}}} = \frac{\partial L}{\partial z{_1}{^{[2]}}}\frac{\partial z{_1}{^{[2]}}}{\partial a{^{[1]}}} +\frac{\partial L}{\partial z{_2}{^{[2]}}}\frac{\partial z{_2}{^{[2]}}}{\partial a{^{[1]}}}= \begin{bmatrix} w{_{11}}{^{[2]}} & w{_{12}}{^{[2]}} \\ w{_{21}}{^{[2]}} & w{_{22}}{^{[2]}} \\ w{_{31}}{^{[2]}} & w{_{32}}{^{[2]}} \\ w{_{41}}{^{[2]}} & w{_{42}}{^{[2]}} \\ \end{bmatrix} \begin{bmatrix} a{_{1}}{^{[2]}}-y \\ a{_{2}}{^{[2]}}-y \\ \end{bmatrix} =w^{[2]T}a^{[2]}
∂ a [ 1 ] ∂ L = ∂ z 1 [ 2 ] ∂ L ∂ a [ 1 ] ∂ z 1 [ 2 ] + ∂ z 2 [ 2 ] ∂ L ∂ a [ 1 ] ∂ z 2 [ 2 ] = ⎣ ⎢ ⎢ ⎡ w 1 1 [ 2 ] w 2 1 [ 2 ] w 3 1 [ 2 ] w 4 1 [ 2 ] w 1 2 [ 2 ] w 2 2 [ 2 ] w 3 2 [ 2 ] w 4 2 [ 2 ] ⎦ ⎥ ⎥ ⎤ [ a 1 [ 2 ] − y a 2 [ 2 ] − y ] = w [ 2 ] T a [ 2 ]
L
L
L
a
[
1
]
a{^{[1]}}
a [ 1 ]
L
L
L
z
[
1
]
z{^{[1]}}
z [ 1 ]
∂
L
∂
z
[
1
]
=
∂
L
∂
a
[
1
]
∂
a
[
1
]
∂
z
[
1
]
=
w
[
2
]
T
a
[
2
]
a
[
1
]
(
1
−
a
[
1
]
)
\frac{\partial L}{\partial z{^{[1]}}}=\frac{\partial L}{\partial a{^{[1]}}} \frac{\partial a{^{[1]}}}{\partial z{^{[1]}}} = w^{[2]T}a^{[2]}a^{[1]}(1-a^{[1]})
∂ z [ 1 ] ∂ L = ∂ a [ 1 ] ∂ L ∂ z [ 1 ] ∂ a [ 1 ] = w [ 2 ] T a [ 2 ] a [ 1 ] ( 1 − a [ 1 ] )
对于输入层与隐含层之间的权重矩阵和隐含层的偏向的求导,方法与上面的一致:
W
i
j
[
1
]
W{_{ij}}{^{[1]}}
W i j [ 1 ]
∂
L
∂
W
i
j
[
1
]
=
∂
L
∂
z
j
[
1
]
∂
z
j
[
1
]
∂
W
i
j
[
1
]
=
w
j
[
2
]
T
a
j
[
2
]
a
j
[
1
]
(
1
−
a
j
[
1
]
)
a
i
[
0
]
T
\frac{\partial L}{\partial W{_{ij}}{^{[1]}}} = \frac{\partial L}{\partial z{_{j}}^{[1]}}\frac{\partial z{_{j}}^{[1]}}{\partial W{_{ij}}{^{[1]}}} = w{_j}{^{[2]T}}a{_j}{^{[2]}}a{_j}{^{[1]}}(1-a{_j}{^{[1]}})a{_{i}}{^{[0]T}}
∂ W i j [ 1 ] ∂ L = ∂ z j [ 1 ] ∂ L ∂ W i j [ 1 ] ∂ z j [ 1 ] = w j [ 2 ] T a j [ 2 ] a j [ 1 ] ( 1 − a j [ 1 ] ) a i [ 0 ] T
对于隐含层偏向
b
j
[
1
]
b{_{j}}{^{[1]}}
b j [ 1 ]
∂
L
∂
b
j
[
1
]
=
∂
L
∂
z
1
[
1
]
∂
z
1
[
1
]
∂
b
j
[
1
]
=
w
j
[
2
]
T
a
j
[
2
]
a
j
[
1
]
(
1
−
a
j
[
1
]
)
\frac{\partial L}{\partial b{_{j}}{^{[1]}}} = \frac{\partial L}{\partial z{_{1}}^{[1]}}\frac{\partial z{_{1}}^{[1]}}{\partial b{_{j}}{^{[1]}}} = w{_j}{^{[2]T}}a{_j}{^{[2]}}a{_j}{^{[1]}}(1-a{_j}{^{[1]}})
∂ b j [ 1 ] ∂ L = ∂ z 1 [ 1 ] ∂ L ∂ b j [ 1 ] ∂ z 1 [ 1 ] = w j [ 2 ] T a j [ 2 ] a j [ 1 ] ( 1 − a j [ 1 ] )
到此,关于神经网络的权重矩阵和偏向的梯度求解全部结束,参数的调整即为:
w
:
w
−
α
∂
J
∂
w
w:w-\alpha\frac{\partial J}{\partial w}
w : w − α ∂ w ∂ J
b
:
b
−
α
∂
J
∂
b
b:b-\alpha\frac{\partial J}{\partial b}
b : b − α ∂ b ∂ J
神经网络在实际使用中,其深度不只有三层,而是大于三层,输入层。隐含层和输出层的结点也都有几十上百个神经元,因此对于一个神经网络来说,模型的参数是庞大的,因此传统的模型在一般的机器上很难快速训练参数,因此在深度神经网络的训练过程中,如何对模型进行优化成为比较现实的问题。1、正则化
J
(
w
,
b
)
=
1
m
∑
L
(
y
,
y
^
)
+
λ
2
m
∑
∣
∣
w
∣
∣
2
J(w,b)=\frac{1}{m} \sum L(y,\hat y)+\frac{\lambda}{2m}\sum||w||{^{2}}
J ( w , b ) = m 1 ∑ L ( y , y ^ ) + 2 m λ ∑ ∣ ∣ w ∣ ∣ 2
λ
2
m
∑
∣
∣
w
∣
∣
2
\frac{\lambda}{2m}\sum||w||{^{2}}
2 m λ ∑ ∣ ∣ w ∣ ∣ 2
λ
\lambda
λ
∂
J
∂
w
=
1
m
∂
L
∂
w
+
λ
m
w
\frac{\partial J}{\partial w}=\frac{1}{m} \frac{\partial L}{\partial w}+\frac{\lambda}{m} w
∂ w ∂ J = m 1 ∂ w ∂ L + m λ w
因此权重矩阵的参数调整为:
w
:
w
−
α
∂
J
∂
w
=
w
−
α
(
1
m
∂
L
∂
w
+
λ
m
w
)
w:w-\alpha\frac{\partial J}{\partial w}=w-\alpha(\frac{1}{m} \frac{\partial L}{\partial w}+\frac{\lambda}{m}w)
w : w − α ∂ w ∂ J = w − α ( m 1 ∂ w ∂ L + m λ w )
=
w
−
α
m
∂
L
∂
w
−
α
λ
m
w
=
(
1
−
α
λ
m
)
w
−
α
m
∂
L
∂
w
=w-\frac{\alpha}{m}\frac{\partial L}{\partial w}-\frac{\alpha \lambda}{m}w=(1-\frac{\alpha \lambda}{m})w-\frac{\alpha}{m}\frac{\partial L}{\partial w}
= w − m α ∂ w ∂ L − m α λ w = ( 1 − m α λ ) w − m α ∂ w ∂ L
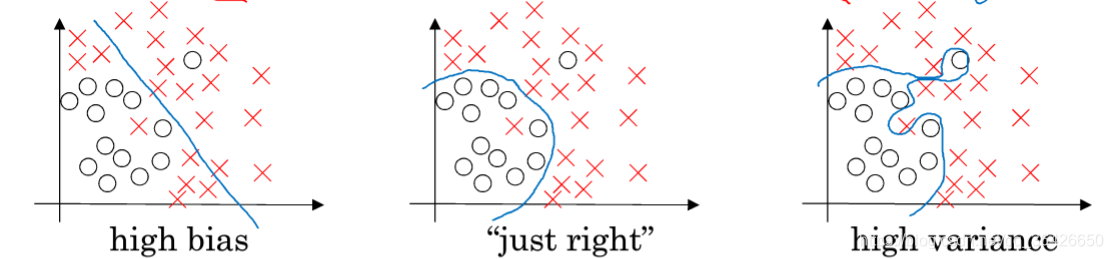
为什么正则化可以防止过拟合?以
t
a
n
h
(
z
)
tanh(z)
t a n h ( z )
z
z
z
λ
\lambda
λ
w
w
w
z
=
w
x
+
b
z=wx+b
z = w x + b
z
z
z 2、激活函数 3、梯度问题
深度神经网络,又称为BP神经网络或者前馈神经网络,其属于标准的神经网络模型,除了这个模型外,还有其他许多类型神经网络。1、循环神经网络RNN 2、卷积神经网络CNN
为了深入学习神经网络的实现过程,本人使用python的TensorFlow框架实现了BP神经网络算法,编程采用python面向对象,程序的运行流程如图:
数据处理
数据处理
读取数据集
训练集
测试集
模型训练
预测
1. main函数 :实现读取训练集和测试集文件,并对数据进行处理(分为训练集X和y、测试集X和y),并调用神经网络类进行训练和预测。
#code by WangJianing
#time:2018.11.24
import tensorflow as tf
import numpy as np
from neural_network import NN
def readFile(filename):
"""
read file from txt
"""
input_x = []
input_y = []
with open(filename,'r') as f:
while True:
line = f.readline()
if line == '':
break
else:
line = line.replace('\n','')
sample = line.split(' ')
x = sample[0:3]
x = list(map(np.float32, x))
y = sample[3]
y = list(map(np.int32, y))
input_x.append(x)
input_y.append(y)
return input_x,input_y
if __name__ == '__main__':
config = tf.ConfigProto()
config.gpu_options.allow_growth = True
config.gpu_options.per_process_gpu_memory_fraction = 0.2 # need ~700MB GPU memory
train_x,train_y = readFile('./data.txt')
test_x,test_y = readFile('./data_test.txt')
sample_size = [len(train_y),len(test_y)]
print(sample_size)
train_x = np.transpose(train_x)
input_y = np.zeros([2,sample_size[0]])
test_x = np.transpose(test_x)
test_y = np.transpose(test_y)
for ei,i in enumerate(train_y):
input_y[i[0]][ei]=1
# print(ei,i)
#build neural network
n = NN(train_x, input_y, test_x, test_y, 'GradientDescentOptimizer', sample_size, config, learning_rate=0.05)
#train
n.train1()
#test
n.test()
2. 神经网络类 :tensorflow创建计算图结点,神经网络参数初始化、前向传播、反向传播、最小化损失函数和梯度下降调参、测试集预测和精度评估。
#code by WangJianing
#time:2018.11.24
import tensorflow as tf
import numpy as np
class NN(object):
"""docstring for NN"""
def __init__(self, train_x, train_y, test_x, test_y, optimize, sample_size, config, learning_rate=0.05):
super(NN, self).__init__()
self.train_x = tf.to_float(train_x, name='ToFloat1')
self.train_y = tf.to_float(train_y, name='ToFloat2')
self.test_x = tf.to_float(test_x, name='ToFloat3')
self.test_y = tf.to_float(test_y, name='ToFloat4')
self.learning_rate = learning_rate
self.optimize = optimize
self.sess = tf.Session()
self.sample_size = sample_size
self.config = config
self.para = [[],[],[],[],0]
self.bildGraph()
# self.train()
def bildGraph(self):
self.parameter_op()
self.towards_op()
self.loss_op()
self.backwords_op()
# self.test_towords()
self.init_op()
def testBuildGraph(self):
self.parameter_op()
self.towards_op()
def parameter_op(self):
self.weight1 = tf.Variable(tf.random_normal([4, 3], stddev=0.03), dtype=tf.float32, name='weight1')
self.bias1 = tf.Variable(tf.random_normal([4, 1]), dtype=tf.float32, name='bias1')
self.weight2 = tf.Variable(tf.random_normal([2, 4], stddev=0.03), dtype=tf.float32, name='weight2')
self.bias2 = tf.Variable(tf.random_normal([2, 1]), dtype=tf.float32, name='bias2')
self.input_xx = tf.Variable(self.train_x,name='xx1')
self.input_xx_test = tf.Variable(self.test_x,name='xx3')
self.input_yy = tf.Variable(self.train_y,name='xx2')
def appendVector(self, v, size, kind):
#该方法是将一个一维向量v复制size次并拼起来
_v = tf.transpose(v)[0]
# print('_v=',_v)
new_v = []
if kind == 0:
for i in range(size):
new_v.append(_v)
self.bias1_train = tf.Variable(new_v, dtype=tf.float32, name='bias1_train')
self.bias1_train = tf.transpose(self.bias1_train)
elif kind == 1:
for i in range(size):
new_v.append(_v)
self.bias2_train = tf.Variable(new_v, dtype=tf.float32, name='bias2_train')
self.bias2_train = tf.transpose(self.bias2_train)
elif kind == 2:
for i in range(size):
new_v.append(_v)
self.bias1_test = tf.Variable(new_v, dtype=tf.float32, name='bias1_test')
self.bias1_test = tf.transpose(self.bias1_test)
elif kind == 3:
for i in range(size):
new_v.append(_v)
self.bias2_test = tf.Variable(new_v, dtype=tf.float32, name='bias2_test')
self.bias2_test = tf.transpose(self.bias2_test)
def towards_op(self):
self.m1 = tf.matmul(self.weight1, self.input_xx, name='matmul1')
# print('m1=',self.m1)
self.appendVector(self.bias1, self.sample_size[0], 0)
# print('self.bias1_train=',self.bias1_train)
self.z1 = tf.add(self.m1 ,self.bias1_train, name='z1')
self.a1 = tf.nn.sigmoid(self.z1,name='a1')
self.appendVector(self.bias2, self.sample_size[0], 1)
self.z2 = tf.add(tf.matmul(self.weight2, self.a1, name='matmul2'),self.bias2_train, name='z2')
self.a2 = tf.transpose(tf.nn.softmax(tf.transpose(self.z2,[1,0]),name='a2'),[1,0])
def test_towords(self):
self.t_m1 = tf.matmul(self.para[0], self.input_xx_test, name='matmul3')
self.appendVector(self.para[2], self.sample_size[1], 2)
self.t_z1 = tf.add(self.t_m1 ,self.bias1_test, name='z1')
self.t_a1 = tf.nn.sigmoid(self.t_z1,name='a1')
self.appendVector(self.para[3], self.sample_size[1], 3)
self.t_z2 = tf.add(tf.matmul(self.para[1], self.t_a1, name='matmul4'),self.bias2_test, name='z2')
self.t_a2 = tf.transpose(tf.nn.softmax(tf.transpose(self.t_z2,[1,0]),name='a2'),[1,0])
def loss_op(self):
self.loss = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(labels=self.train_y, logits=self.a2))
self.optimizer = tf.train.GradientDescentOptimizer(self.learning_rate)
def backwords_op(self):
self.train = self.optimizer.minimize(self.loss)
def train1(self):
with tf.Session(config=tf.ConfigProto(gpu_options=tf.GPUOptions(per_process_gpu_memory_fraction=0.333))) as sess:
sess.run(self.init_op)
for i in range(10):
sess.run(self.train)
self.para = [sess.run(self.weight1),sess.run(self.weight2),sess.run(self.bias1),sess.run(self.bias2),sess.run(self.loss)]
print("==========step",i,"==========")
print("weight1:\n",self.para[0],"\nb1:\n",self.para[2])
print("\nweight2:\n",self.para[1],"\nb2:\n",self.para[3])
print("\nloss=",self.para[4])
def init_op(self):
self.init_op = tf.global_variables_initializer()
def test(self):
self.test_towords()
with tf.Session(config=tf.ConfigProto(gpu_options=tf.GPUOptions(per_process_gpu_memory_fraction=0.333))) as sess:
sess.run(tf.global_variables_initializer())
sess.run([self.bias1_test,self.bias2_test])
#每个样本的每个类标取值的概率
predict_proba = sess.run(self.t_a2)
#预测每个样本的类标(0或1)
predict_proba = np.transpose(predict_proba)
print('\npredict_proba=',predict_proba)
predict_value = np.argmax(predict_proba,axis=1)
print('\npredic_value=',predict_value)
#计算准确率:
# accuracy = 0
# # print(test_y[0][0])
# for ei,i in enumerate(predict_value):
# if i == self.test_y[0][ei]:
# accuracy += 1
# accuracy /= sample_size
# print('\naccuracy=',accuracy)
本人在编写本博文大概花了一周时间,经过对深度学习的常用模型——神经网络的原理理解、模型训练的推导以及最后程序编写,能够更加深刻的理解神经网络模型,这对今后学习机器学习、深度学习以及涉及到相关应用时具有很大的作用。
博客记录着学习的脚步,分享着最新的技术,非常感谢您的阅读,本博客将不断进行更新,希望能够给您在技术上带来帮助。