Leetcode10.正则表达式匹配——动态规划之一个模型三个特征

引入

Leetcode中遇到了这样一道题：

10.正则表达式匹配
给你一个字符串 s 和一个字符规律 p，请你来实现一个支持 ‘.’ 和 ‘’ 的正则表达式匹配。
‘.’ 匹配任意单个字符
'’ 匹配零个或多个前面的那一个元素
所谓匹配，是要涵盖 整个 字符串 s的，而不是部分字符串。

在分析这道题的时候，很容易的就想到去挨个匹配，字符串s的第一个匹配字符串p的第一个，如果遇到.就跳过一个字母，遇到*情况就复杂一些，因为要去查看后续子串的匹配。

所以这样很容易想到，第一个方法：回溯。然而回溯需要判断的条件太多，并且比较难以想出来，其解法可以去题目里参考官方题解。

这里，我们介绍动态规划。动态规划除了在常见的“图”求最小距离，或者数组（“阶梯”）求最小步数，在某些题目中使用往往有惊艳的效果。
比如171.周赛题目1320. 二指输入的的最小距离就是用动态规划来做的。
又比如本题，用动态规划往往更好理解。

“一个模型三个特征”理论

动态规划作为一个非常成熟的算法思想，很多人对此做了非常全面的总结，我把这部分理论总结为“一个模型三个特征”。

首先，“一个模型”指的是动态规划适合解决问题的模型。我把这个模型定义为“多阶段决策最优解模型”。

具体来说，我们一般是用动态规划来解决最优问题。而解决问题的过程，需要经历多个决策阶段。每个决策阶段都对应一组状态。然后我们寻找一组决策序列，经过这组决策序列，能够产生最终期望求解的最优值。

“三个特征”，分别是最优子结构、无后效性和重复子问题。这三个概念比较抽象，逐一解释一下。

1. 最优子结构
   最优子结构指的是，问题的最优解包含子问题的最优解。反过来说就是，我们可以通过子问题的最优解，推导出问题的最优解。如果我们把最优子结构，对应到我们前面定义的动态规划问题模型上，那我们也可以理解为，后面阶段的状态可以通过前面状态推导出来。
2. 无后效性
   无后效性，有两层含义，第一层含义是，在推导后面阶段状态的时候，我们只关心前面阶段的状态值，不关心这个状态是怎么一步步推导出来的。第二层含义是，某阶段状态一旦确定，就不受之后阶段的决策影响。无后效性是一个非常“宽松”的要求。只要满足前面提到的动态规划问题模型，其实基本上都会满足无后效性。
3. 重复子问题
   这个概念，前面一节，已经多次提到。用一句话概括就是： 不同的决策序列，到达某个相同的阶段时，可能会产生重复的状态。

回到我们的图问题：假设我们有一个 n 乘以 n 的矩阵 w[n][n]。矩阵存储的都是正整数。棋子起始位置在左上角，终止位置在右下角。我们将棋子从左上角移到右下角。每次只能向右或者向下移动一位。整个过程，会有多种不同的路径可以选择。我们把每条路径经过的数字加起来看作路径的长度。那从左上角到右下角的最短路径长度是多少呢？

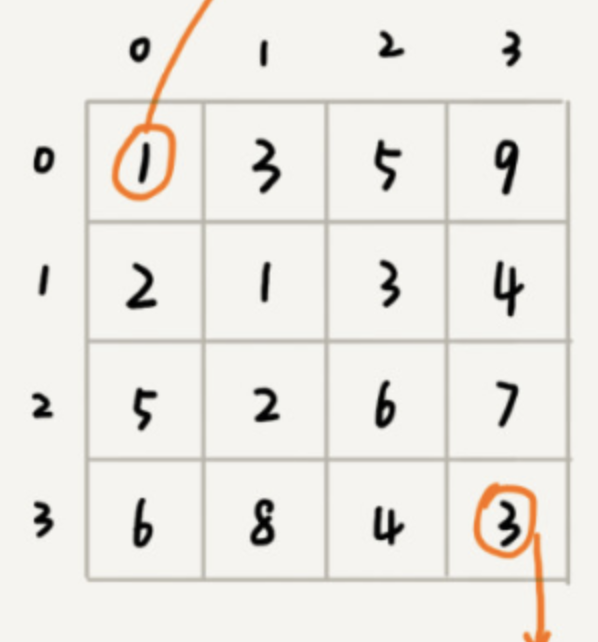
我们先看看，这个问题是否符合“一个模型”？

• 从 $（0, 0）$直到 $（n-1, n-1）$，总共要走 $2*（n-1）$步，也就是对应着 $2*（n-1）$个阶段。每个阶段都有向右走或者向下走两种决策，并且每个阶段都会对应一个状态集合。

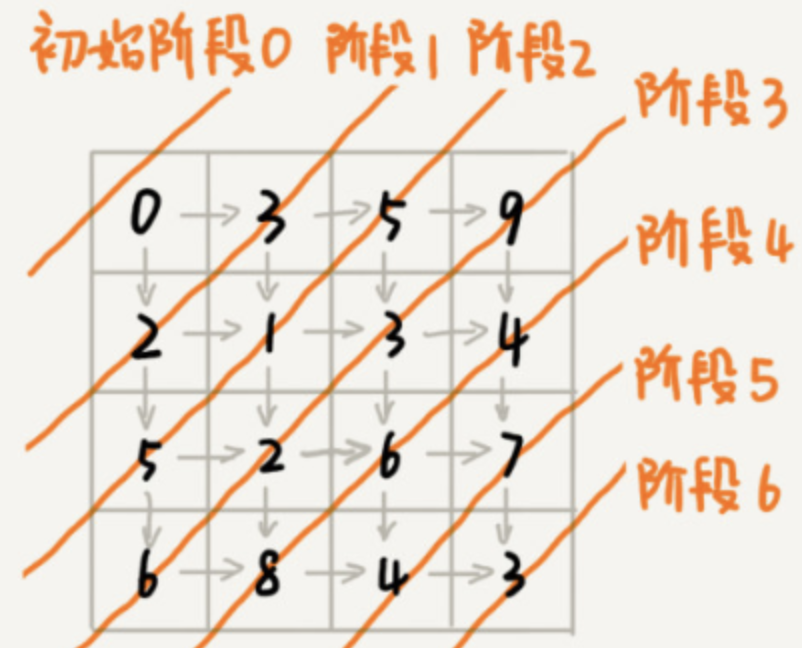
所以，这个问题是一个多阶段决策最优解的问题，符合动态规划的模型。

再来看，这个问题是否符合 “三个特征” ？

• 我们可以用回溯算法来解决这个问题。如果你自己写一下代码，画一下递归树，就会发现，递归树中有重复的节点。重复的节点表示，从左上角节点对应的位置，有多种路线，这也能说明这个问题中存在重复子问题。

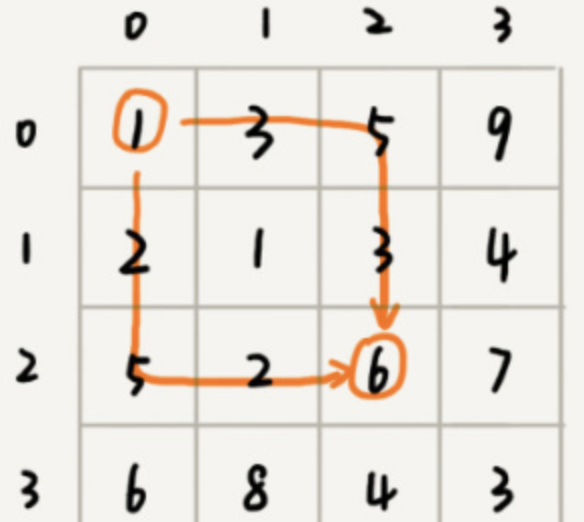
• 如果我们走到（i, j）这个位置，我们只能通过（i-1, j）,（i, j-1）这两个位置移过来，也就是说，我们想要计算（i, j）位置对应的状态，只需要关心（i-1, j）,（i, j-1）这两个位置的状态，并不关心棋子是通过什么样的路线到达这两个位置的。而且，我们仅仅允许往下和往右移动，不允许后退，所以，前面阶段的状态确定之后，不会被后面阶段的决策所改变。所以这个问题，是符合“无后效性”的。

• 刚刚定义状态的时候，我们把从起始位置（0, 0）到（i, j）的最小，记作 min_dis(i, j)。因为我们只能往右或者往下移动，所以，我们只有可能从（i-1, j）,（i, j-1）两个位置到达（i, j）。也就是说，到达（i, j）的最短路径要么经过（i-1, j），要么经过（i, j-1），而且到达（i, j）的最短路径肯定包含到达这两个位置的最短路径之一。换句话说就是，min_dis(i, j)可以通过min_dis(i, j-1)和min_dis(i-1, j)两个状态推导出来。这就说明，这个问题符合“最优子结构”。

动态规划一般是通过状态转移方程来解决的。
比如：min_dist(i, j) = w[i][j] + min(min_dist(i, j-1), min_dist(i-1, j))。
所以解决动态规划问题，最重要的就是找到它的状态转移方程。

Leetcode题解

因为题目拥有 最优子结构 ，一个自然的想法是将中间结果保存起来。我们通过用 dp(i,j)表示 s 的前 i 个是否能被 p 的前 j 个匹配。我们可以用更短的字符串匹配问题来表示原本的问题。也就是需要一个m*n的dp数组来存储每一位的匹配结果。 由于只用保存是否匹配，所以用bool值就可以。

转移方程

怎么想转移方程？首先想的时候从已经求出了 dp[i-1][j-1] 入手，再加上已知 s[i]、p[j]，要想的问题就是怎么去求 dp[i][j]。

已知 dp[i-1][j-1] 意思就是前面子串都匹配上了，不知道新的一位的情况。
那就分情况考虑，所以对于新的一位 p[j] s[i] 的值不同，要分情况讨论：

1. 相同字符的匹配，即p[j] == s[i]，那么直接可以推出dp[i][j] = dp[i-1][j-1]。
2. 字符与.的匹配，即p[j]=='.'，那么也可以推出dp[i][j] = dp[i-1][j-1]。
3. 最难的一种情况，即p[j] ==" * "。我们单独细说。

首先给了*，明白 *的含义是匹配零个或多个前面的那一个元素，所以要考虑他前面的元素p[j-1]。*跟着他前一个字符走，前一个能匹配上 s[i]，* 才能有用，前一个都不能匹配上 s[i]，*也无能为力，只能让前一个字符消失，也就是匹配 00 次前一个字符。
所以按照 p[j-1] 和 s[i] 是否相等，我们分为两种情况：

1. 如果p[j-1] != s[i] ，那么可以推出：dp[i][j] = dp[i][j-2]。
   比如(ab, abc * )。遇到 * 往前看两个，发现前面 s[i] 的 ab 对 p[j-2] 的 ab 能匹配，虽然后面是 c*，但是可以看做匹配 0次 c， 相当于直接去掉 c * ，所以也是 True。
   但需要注意 (ab, abc**) 是 False。这种情况需要再判断。
2. p[j-1] == s[i] 或者 p[j-1] == "."，表示*前面那个字符，能匹配 s[i]，或者 * 前面那个字符是万能的 .，那么*是必然能够向后匹配的。该情况转移方程需要分三种情况讨论。

上述情况2的转移方程：

• dp[i][j] = dp[i-1][j] ，即多个字符匹配的情况 。如果后面匹配了多个p[j-1]的字符，那么，相当于不消耗p的字符，直接将s的字符向后移。对应的就是s的前i个、s的前i-1个与p的前j个的匹配结果相同。
• dp[i][j] = dp[i][j-1]。单个字符匹配的话，比如(ac,a*c)，相当于去掉p中的*，只匹配两个ac。所以消耗了一个*字符。
• dp[i][j] = dp[i][j-2] 。表示没有匹配的情况，与之前的情况1一样，相当于匹配了0次，相当于直接去掉 c *。

最后，其代码如下：

public boolean isMatch(String s,String p){
            if (s == null || p == null) {
                return false;
            }
            boolean[][] dp = new boolean[s.length() + 1][p.length() + 1];
            dp[0][0] = true;//dp[i][j] 表示 s 的前 i 个是否能被 p 的前 j 个匹配
            for (int i = 0; i < p.length(); i++) { // here's the p's length, not s's
                if (p.charAt(i) == '*' && dp[0][i - 1]) {
                    dp[0][i + 1] = true; // here's y axis should be i+1
                }
            }
            for (int i = 0; i < s.length(); i++) {
                for (int j = 0; j < p.length(); j++) {
                    if (p.charAt(j) == '.' || p.charAt(j) == s.charAt(i)) {//如果是任意元素 或者是对于元素匹配
                        dp[i + 1][j + 1] = dp[i][j];
                    }
                    if (p.charAt(j) == '*') {
                        if (p.charAt(j - 1) != s.charAt(i) && p.charAt(j - 1) != '.') {//如果前一个元素不匹配 且不为任意元素
                            dp[i + 1][j + 1] = dp[i + 1][j - 1];
                        } else {
                            dp[i + 1][j + 1] = (dp[i + 1][j] || dp[i][j + 1] || dp[i + 1][j - 1]);
                            /*
                            dp[i][j] = dp[i-1][j] // 多个字符匹配的情况	
                            or dp[i][j] = dp[i][j-1] // 单个字符匹配的情况
                            or dp[i][j] = dp[i][j-2] // 没有匹配的情况
                             */
                            
                        }
                    }
                }
            }
            return dp[s.length()][p.length()];
        }