接着上一次的kruskal算法,这次讲更高级的prim算法
#Prim Algorithm prim算法和经典的Dijkstra最短路径寻路算法惊人的相似，都是采用层层扩散的方式收敛出树。同时又与kruskal算法分享着类似的逻辑。关于Dijkstra算法敬请参考之前发布的《SPF算法完美教程》，如果没听过它也无碍，prim算法将展示它的思想。 前提准备：总共n个节点编号，放入集合甲中，设一个集合乙用来存放生成树成长过程中依次覆盖的节点，记这棵生成树年轻时为T。（注意，这是个动态生长的树，从0开始直到长成最小生成树） Prim算法的基本流程（一个周期）：（同kruskal一样也是通过一个个简单的循环来完成的） 首先,从甲中取出一个距离T最短的节点Q，就是乙中所有节点的所有外部邻居中最近的那个点，如果是第一次循环的话就从甲中随机取出一点。（若是并列最短就随便选）。然后将这个点加入到乙中。以此循环直到甲空掉了为止。 (@ο@) 哇～是不是感觉比kruskal算法还要简单直接，流程图都不需要画了（因为是一条笔直的直线流程），如果将各个循环结束时的状态图记录下来，就会看到一棵生成树从小长到大的过程。如同这个动态图：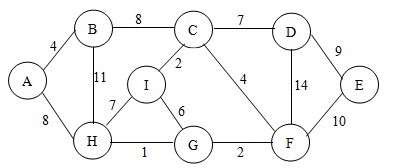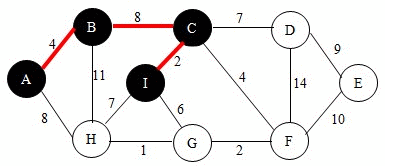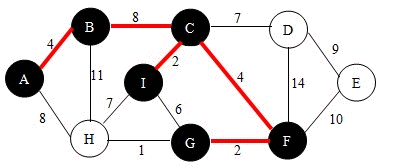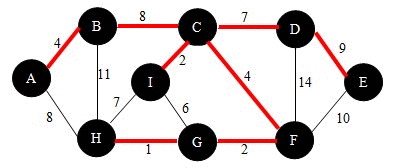 
##有待调用的重要前提：
在证明prim算法之前我们需要用到一个底层结论：在一个连通图G中，对于每个点，与自己相连的最短边一定属于G的生成树。（如果有并列则任意一个最短边） 这个结论very重要，想要证明他也很easy，还是用万能的反证法： 对于一个点Q它连接着m条边，其中有一条最短边L，G的最小生成树T不经过L，那么对于Q剩下m-1条边中至少有一条边连接Q与T，设有z条这样的边（0<z<m）。 那么如果此时在T中把Q及Q连接的m条边都移除，T剩下的部分将被分成z个相互隔离的部分（生成树的特性），而且Q关于L对称的那个点有且只有属于z个部分中的某一个部分。那么问题来了，属于的那个部分与Q相连的边应当被替换成开销更小的L，所以与T是最小生成树矛盾，得以反证。 上图解（图中z=3）：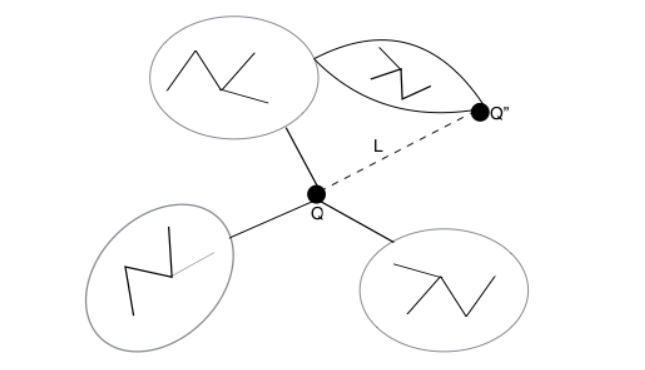 
这样就一清二楚了（吧？），图中各个区域的“树枝”符号就代表了被分割的部分树，他们之间只能通过Q相通。所以Q的最短边L必然在真正的生成树中。
##数学归纳法证明：
有了这个结论后大势已定，接下来我将展示用经典的数学归纳法证明prim算法，其中以集合乙中的节点数量为递增变量（所以这里的n是动态的），也可以看成是动态增长的树T。 n=1，选择任意一个点Q1。 n=2，Q1发散到最近的Q2其中边L1属于最终最小生成树T，成立。 假设n=k的时候成立，也就是Q1Q2Q3一直到Qk所在的T属于最终最小生成树。 那么接下来做一个惊人之举：把此时的T整体看成一个节点。为什么可以这么看呢，因为T和一个节点share共同的属性：都是属于最终生成树；都有若干个与自己相连的边。因而此举不影响最后的生成树。记住，最小生成树的根本目的和原则就是想方设法不择手段地用最少的边连接最多的节点！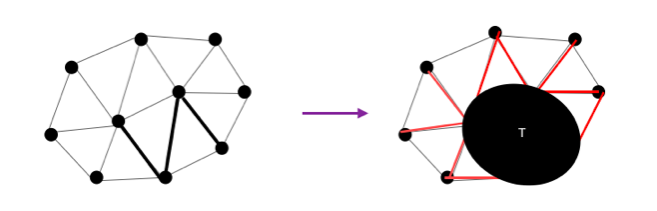 
当n=k+1的时候，从甲中剩下的节点中选择距离T（点）最近的一条边Lk加入到乙中，根据之前定理，T+Lk一起也属于最终生成树。成立。 由数学归纳法得证prim算法的正确性。完。
##最后，两种算法的异同
不难看出，两种基本算法的内容都通俗易懂，只是证明起来略有困难。两者的区别在于，kruskal基于边来收敛，而prim基于点。但是综合来看prim要比kruskal高级一点，在边数比较稠密的情况下用prim求生成树要快于kruskal，因为kruskal是一条边一条边来找的，毕竟prim使用和Dijkstra相似的“堆栈”思想而kruskal是一种贪心算法，当边稀疏时两者都可适用。Anyway，二者都是图论学中非常重要的算法，大家务必牢记！