现代量子计算入门

现代量子计算入门

---

在写作完成现代量子计算入门(事实上是我<<现代量子密码学>>的大作业)时,我想秉承一个基本的主线:沿着量子计算的概念从基本的Qubit开始,直到应用的Grover算法,这条主线不算长,也不算深入,但是也算是对量子计算有了一个入门的认识;此外事实上还有另一条附属线:那就是对量子计算的编程实现,因为我一直认为实践很重要,有可能在理解理论的时候已经感觉很清晰了,但是在编程计算的时候可能会陷入糊涂.因此实践可以帮助理解得更深入;

经典的计算机概念和量子计算的概念的对应也是一个非常重要的理解手段,因为我们会发现在量子计算电路和很多应用的设计时,首先会优先满足普通电路的功能,再谋求量子计算特性的那些超常功能;

注:
本文的撰写过程中大量参考了博客: https://www.cnblogs.com/zmzzzz/p/11369637.html
以及QuSim的代码: https://github.com/adamisntdead/QuSimPy/blob/master/QuSim.py

---

Q比特(Qubit)

量子比特是量子计算的最基本单位,就像经典计算的基本单位比特一样.但是量子比特,也就是狄拉克符号,其表征意义却丰富很多, $|0\rangle$和 $|1\rangle$是常用的两个量子比特,它们的概率组合即所谓的叠加态:

$S = \alpha_0 | 0\rangle +\alpha_1 | 1\rangle$

从量子比特的概念其实即可一窥量子计算的优势:原子具有在同一时刻处于两个不同位置、又同时向上下两个相反方向旋转的特性,称为“量子超态”.而一旦有外力干扰,模糊运动的原子又可以马上归于准确的定位(即回归确定的状态).这种似是而非的混沌状态与人们熟知的常识相矛盾,但如果利用其表达信息,却能发挥出其瞬息之间千变万化而又万变不离其宗的奇效.因为当许多个量子状态的原子纠缠在一起时,它们又因量子位的“叠加性”,可以同时一起展开“并行计算”,展现出强大的算力.

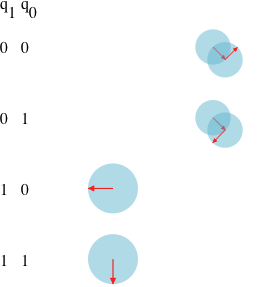
事实上 $|0\rangle$和 $|1\rangle$的实际物理意义是可以指派的,它们可以表征物理实体比如光的偏振状态是横的还是纵的,二维空间的正交基,氢原子的电子在基态还是激发态,亦或者薛定谔的猫的生死状态等等… …一句话总结,就是狄拉克符号事实上屏蔽了底层物理状态的一些难以用数学解释的现象(其实就是叠加状态),使得这些物理现象的基础上可以引入更复杂的数学工具来推演这些现象,也就是量子计算;

事实上,在这个二维空间中不止一组标准正交基,还存在 $|+\rangle = \frac{1}{\sqrt2}|0\rangle + \frac{1}{\sqrt2}|1\rangle$和 $|-\rangle = \frac{1}{\sqrt2}|0\rangle - \frac{1}{\sqrt2}|1\rangle$,称之为sign basis,而 $| 0\rangle$和 $|1\rangle$称之为standard basis;

值得注意的是:叠加态是一种物理事实,但是并不能被观测.在没有进行测量的时候,粒子可能是 $|0\rangle$也可能是 $|1\rangle$ ,但是当测量进行之后了,粒子就会以 $\alpha_0$的平方概率确定自己在 $|0\rangle$状态,或者以 $\alpha_1$的平方概率确定自己在 $|1\rangle$状态,无论结果是什么,粒子会确定一个状态,再次测量也不会变.

关于多比特的量子系统

以上我们讨论了单量子比特的系统,有 $|0\rangle$和 $|1\rangle$两种可能,用 $S=\alpha_0 | 0\rangle +\alpha_1 | 1\rangle$描述.而双量子比特的系统有 $|0\rangle|0\rangle,|0\rangle|1\rangle,|1\rangle|0\rangle,|1\rangle|1\rangle$四种可能,以此类推, $n$量子比特的系统有 $|x_1...x_n\rangle$的 $2^n$种可能的状态,其中 $x_i \in \{0,1\}$,这些状态蕴藏了强大的算力;

双量子比特系统都可以分解成两个单量子比特系统的乘积形式吗?不能;

比如著名的Bell态不可分解为两个单量子比特系统的乘积形式: $\frac{1}{\sqrt2}|00\rangle + \frac{1}{\sqrt2}|11\rangle$;以此可以引申出一个定义:

定义(纠缠态):对于这样无法分成两个单独的系统来描述的系统(形如 $\rho_{\mathrm{AB}}=\sum_{\mathrm{k}} p_{k} \rho_{k}^{A} \otimes \rho_{k}^{B}$),我们称这样的态为纠缠态;

其中,两个量子系统A和B的联合状态为 $\rho_{\mathrm{AB}}$,单独的状态为 $\rho_{\mathrm{A}}$和 $\rho_{\mathrm{B}}$,而 $\sum_{\mathrm{k}} p_{k}=1$;

量子比特系统的编程实现,这里以 $|00000\rangle$为例,我们知道对 $|0\rangle$作五次张量积之后其只剩下第一位为 $1$,因此:

NUM_OF_QUBITS = 5;
INIT_STATE    = np.zeros(2**NUM_OF_QUBITS);
INIT_STATE[0] = 1;

---

EPR佯谬

EPR佯谬(Einstein-Podolsky-Rosen paradox) 是E.爱因斯坦,P.波多尔斯基和R.罗森1935年为论证量子力学的不完备性而提出的一个悖论.EPR是这三位物理学家姓氏的首字母缩写.这一悖论涉及到如何理解微观物理实在的问题.爱因斯坦等人认为,如果一个物理理论对物理实在的描述是完备的,那么物理实在的每个要素都必须在其中有它的对应量,即完备性判据.当我们不对体系进行任何干扰,却能确定地预言某个物理量的值时,必定存在着一个物理实在的要素对应于这个物理量,即实在性判据.他们认为,量子力学不满足这些判据,所以是不完备的.因此可见这个悖论是提出来抨击量子力学的不合理性的,但是事实却是,这个悖论本身是错的,并且反而促成了量子原理里量子纠缠理论的发展.EPR佯谬是建立在Heisenberg不确定性原理之上的:

Heisenberg不确定性原理(Heisenberg Uncertainty Principle) 即不可能同时知道一个粒子的位置和它的速度,粒子位置的不确定性,必然大于或等于普朗克常数(Planck Constant)除 $4\pi$( $\delta x\delta p\le h/4\pi$),这表明微观世界的粒子行为与宏观物质很不一样.

现在假设有如下状态的粒子:

$|\psi\rangle =\alpha_0 |0\rangle +\alpha_1 | 1\rangle=\beta_0 | +\rangle +\beta_1 | -\rangle$

现在Heisenberg不确定性原理意味着粒子的位置与动量不可同时被确定,位置的不确定性越小,则动量的不确定性越大,反之亦然.也就是我们只能选择知晓其中位置和运动信息中的一个量,并且在知晓后另一个是更加不能被确定的.就上述粒子来说,当我们确定了其在 $|0\rangle$和 $|1\rangle$这组基下测量有了具体的值,就不可能同时在 $|+\rangle$和 $|-\rangle$这组基下有确定的值.我们将 $|\alpha_0\rangle| + | \alpha_1\rangle|$称为Uncertainty in Position,记作 $S_{\alpha}$,将 $|\beta_0\rangle| + | \beta_1\rangle|$称为Uncertainty in Momentum,记作 $S_{\beta}$.那么不确定性原理的数学表示是: $S_{\alpha}S_{\beta}>=\sqrt2$,也就是我们不可能同时接近 $1$地确定一个量子在standard basis和sign basis的值.

EPR佯谬的基本思路(basic idea) 首先是相对论的基本假设,即, $\forall$物质或者作用的传播速度不能超过光速;其次,定域性理论,即,一个物体只能被周围的力量影响,如果某一点产生的效应,要影响到另一点,在中间的空间,例如场,会成为运动的中介.因此综合上述,假设存在一对相距距离很远的粒子,比如在宇宙的两端,那么其中一个产生变化的话如果要影响到另一个则需要一定的时间间隔 $\delta t$;

但是定域性原理套用在量子的情况上是有问题的,因为量子具有非局域性原理,一对粒子隔得再远,他们的相互影响也可以瞬间完成,这种超距作用即称为量子纠缠.但是值得注意的是量子纠缠并未违背爱因斯坦相对论中信息不能超光速传播的前提:假设存在一对相距很远的量子比特A,B;虽然无论位于A的人 $P_A$测量A的结果是什么, $P_B$都可以马上知道,但是能拿这个传递信息吗？不能,因为在测量之前, $P_A$也不知道测量A的结果是什么,也就无法约定好测出什么结果时对应什么信息,也就无法根据其状态传递信息.

---

量子逻辑门及电路

量子比特实现了用向量来表征,因为量子比特的演化是线性的,所以在量子比特上的操作,就可以用矩阵来表示.单量子比特的维度是 $\mathbb{R}^{2\times 1}$,因此单量子比特门的维度是 $\mathbb{R}^{2\times 2}$,例如 $U= [ \begin{matrix} {\frac{1}{\sqrt2}} &{-\frac{1}{\sqrt2}} \\ {\frac{1}{\sqrt2}}&{\frac{1}{\sqrt2}} \end{matrix}]$可以把 $[1,0]$变到 $[{\frac{1}{\sqrt2}},{\frac{1}{\sqrt2}}]$;

对于双量子比特系统来说,他们的状态是 $\alpha_{00} | 00\rangle+\alpha_{01} | 01\rangle+\alpha_{10} | 10\rangle+\alpha_{11} | 11\rangle$,需要用 $\mathbb{R}^{4\times 1}$的向量来描述,也就是 $[ \begin{matrix} {\alpha_{00}} \ {\alpha_{01}} \ {\alpha_{10}} \ {\alpha_{11}} \end{matrix}]$,对应操作双量子比特的逻辑门就是用 $\mathbb{R}^{4\times 4}$的矩阵了.在明确了量子逻辑门的本质后,值得注意的是量子电路的两个特点:

• 量子态的叠加性(Superposition Principle):一个量子比特就是Hilbert空间中 $\mathbb{R}^{2}$的向量,两个量子比特就是Hilbert空间中 $\mathbb{R}^{4}$的向量,3个量子比特就是Hilbert空间中 $\mathbb{R}^{8}$的向量,… …, $n$个量子比特就是Hilbert空间中 $\mathbb{R}^{2^n}$的向量.

• 量子电路的可逆性(Unitary Evolution):经典电路没有可逆的特性,比如OR门,如果输出是 $１$,但是输入是无法确定的: $(1,1),(1,0),(0,1)$都有可能,因为信息丢失了.而量子的操作变换则必须是酉变换(Unitary Transformation:是保内积的,两个向量在乘以相同的 $U$后,他们的内积不变),即可逆,可以根据输出的信息反推输入.

一些经典的单量子逻辑门及其实现

X门又称为比特翻转,他可以把 $|0\rangle$变成 $|1\rangle$,把 $|1\rangle$变成 $|0\rangle$:

$X=[ \begin{matrix} {0} &{1} \\ {1}&{0} \end{matrix}]$

$Y=[ \begin{matrix} {0} &{-i} \\ {i}&{0} \end{matrix}]$

Z门又称为相位翻转门,可以把 $|+\rangle$变成 $|-\rangle$, $-|1\rangle$变成 $|1\rangle$:

$Z=[ \begin{matrix}{}{1} &{0} \\ {0}&{-1} \end{matrix}]$

Hadamard门,作用是把 $|1\rangle$变成 $|-\rangle$, $|0\rangle$变成 $|+\rangle$:

$H=[ \begin{matrix} {\frac{1}{\sqrt2}} &{\frac{1}{\sqrt2}} \\ {\frac{1}{\sqrt2}}&{-\frac{1}{\sqrt2}} \end{matrix}]$

总之会有很多的量子逻辑门以及他们的组合,而为它们每一个编写一个函数实现是很没效率的,又因为我们提到了每个单量子逻辑门都是维度是 $\mathbb{R}^{2\times 2}$的矩阵,因此基本思路是编写一个字典(map)来通过(名称:矩阵)的key-value对来实现多种量子逻辑门:

singleQubitGates = {
        # Pauli-X / Not Gate
        'X': np.matrix([
            [0, 1],
            [1, 0]
        ]),
        # Pauli-Y Gate
        'Y': np.matrix([
            [0, -i],
            [i, 0]
        ]),
        # Pauli-Z Gate
        'Z': np.matrix([
            [1, 0],
            [0, -1]
        ]),
        # Hadamard Gate
        'H': np.multiply(1. / np.sqrt(2), np.matrix([
            [1, 1],
            [1, -1]
        ])),
... ...
        'TDagger': np.matrix([
            [1, 0],
            [0, np.e**(i * np.pi / 4.)]
        ]).conjugate().transpose()
    }

---

Hadamard门

Hadamard门(Hadamard gate),简称 $H$.事实上它是这样的一个变换:

$H={\frac{1}{\sqrt2}}[ \begin{matrix} 1 &1 \\ 1&-1 \end{matrix}]$
多量子逻辑门其实是单量子逻辑门的张量积,因此多量子比特的Hadamard门把每一个量子比特都由 $|1\rangle$变成 $|-\rangle$, $|0\rangle$变成 $|+\rangle$.因此这 $n$比特的Hadamard门就可以记为 $H^{\otimes n}$,矩阵表达如下:

$H^{\otimes n}=[ \begin{matrix} {\frac{1}{\sqrt2}} &{\frac{1}{\sqrt2}} \\ {\frac{1}{\sqrt2}}&{-\frac{1}{\sqrt2}} \end{matrix}] \otimes ……\otimes [ \begin{matrix} {\frac{1}{\sqrt2}} &{\frac{1}{\sqrt2}} \\ {\frac{1}{\sqrt2}}&{-\frac{1}{\sqrt2}} \end{matrix}]$

因此我们对于单量子比特有:

$H:|0\rangle \mapsto \frac{1}{\sqrt2}|0\rangle+\frac{1}{\sqrt2}|1\rangle$

对于双量子比特有:

$H^{\otimes 2}:|00\rangle \mapsto (\frac{1}{\sqrt2}|0\rangle+\frac{1}{\sqrt2}|1\rangle)(\frac{1}{\sqrt2}|0\rangle+\frac{1}{\sqrt2}|1\rangle)$

依此类推,我们对于 $n$量子比特有(类比二项式展开):

$H^{\otimes n}:|00\cdots 0\rangle \mapsto \frac{1}{2^{\frac{n}{2}}} \sum_{x \in \{0,1 \}^n}|x\rangle$

多量子比特的Hadamard门实现

综上所述我们发现应该根据已知的量子比特的数目 $n$来构造 $H^{\otimes n}$,这里主要用到了张量积操作和python的reduce函数:他可以把一个序列的操作依此施加在一个初始输入上(就是map-reduce的reduce):

def Generate_Gate(self,NUM_OF_QUBITS,qubit1,qubit2=1):
    Identity      = np.eye(2);
    HGate         = np.multiply(1. / np.sqrt(2), np.matrix([[1, 1],[1, -1]]));
    GateOrder     = (HGate if i == qubit1 else Identity
                    for i in range(1, NUM_OF_QUBITS + 1));
    GateMatrix    = reduce(np.kron, GateOrder);
    return GateMatrix;

那么我们接下来构造 $n$个量子比特 $|0\rangle$,其实也就是Simon’s Algorithm 和 Grover Algorithm的第一步,基本上所有的量子算法不管要干嘛,都会先使用一个Hadamard门,毕竟Hadamard门是用 $n$比特构造同时表达 $2^n$个数据的重要工具.总之过程和输出如下(这里 $n=5$):

NUM_OF_QUBITS = 5;
INIT_STATE    = np.zeros(2**NUM_OF_QUBITS);
INIT_STATE[0] = 1;
gate  = Gate('H');
H_MAT = gate.Generate_Gate('H',NUM_OF_QUBITS,1);
AVE_STATE     = np.dot( H_MAT,INIT_STATE  );
print(AVE_STATE);

输出为:

[[0.70710678 0.         0.         0.         0.         0.
  0.         0.         0.         0.         0.         0.
  0.         0.         0.         0.         0.70710678 0.
  0.         0.         0.         0.         0.         0.
  0.         0.         0.         0.         0.         0.
  0.         0.        ]]

---

Simon’s Algorithm 到 Grover Algorithm

Simon’s Algorithm的问题定义:

有一个secret string $s$,是 $n$位的 $0,1$串 $s \in \{0,1 \}^n$,现在有一个黑盒子 $f(x)$,我们对他唯一的了解就是 $f(x)=f(x \otimes s)$,输入的 $x$也是 $n$位的 $0,1$串 $x \in \{0,1 \}^n$.请问,要多少次,我们可以找到这个secret string?

(经典的解决思路) 如果我们能找到 $x$和 $x \otimes s$,那么非常容易,就可以得到 $s$,只要 $x \otimes x \otimes s$,也就是假如找到了,就异或操作重复一次即可得到 $s$.如何找到两个输入拥有相同的输出?事实上,由于 $n$位的 $0,1$串 $x \in \{0,1 \}^n$取自有限的集合,那么和生日碰撞问题一样(密码学里经常用来解释hash code的映射能力的一个现实问题),“一群人中,要多少人就有两个人的生日是相同的,23人两个人的生日是相同的概率就大于50%了,如果有60个人,那么两个人生日相同的概率就超过99%了…”,那么本问题的思路也一样,只要搜索足够多次 $x$,也就大概率能找到,这个搜索次数的阈值实际上是 $2^{n/2}$次.

(量子解法思路) 其实就是构造一个关于 $s·x=0$的线性方程组,然后解这个方程组,由于量子算法中的测量是基于概率的,因此事实上在构造这个方程组的每一行时,有可能会得到和已经存在的行 $s_1x_1^1+s_2x_2^1+……+s_nx_n^1 =0 \mod 2$一样或者线性相关的行,这时候算法就会失败,因为解不出来 $s$.总之,算法总共分三步:

• (构造叠加态):构造随机叠加态 $\frac{1}{\sqrt2} |r\rangle +\frac{1}{\sqrt2} |r \oplus s \rangle$,其中 $r$是任意的一个序列,它是 $\frac{1}{2^{\frac{n}{2}}} \sum_x |x\rangle$和 $|b\rangle$一起通过 $U_f$之后测量到的结果;
• (Fourier Sample):做Fourier Sample得到随机的 $y: y·s=0(mod2)$(这就得到了方程组的其中一行);
• (构造线性方程组):重复 $n-1$次来生成 $n-1$次的线性方程组,并解线性方程组来得到 $s$.

Grover Algorithm的问题定义:

现在有这样一个内部机制不明确的函数: $f: \{ 0,1,2,3,……,N-1 \} \rightarrow \{0,1\}$.我们的目标是找到那些满足 $f(x)=1$的 $x$;

**(经典的解决思路)**其实就是一个搜索问题,最坏的前提就是只有一个满足 $f(x)=1$的 $x$(记为 $x^*$),那么无论采用二分搜索还是其他方法,平均需要搜索 $N/2$次方能找到 $x^*$;

**(量子解法思路)**其实就是相位翻转再加对于平均值翻转,不断地放大满足 $f(x^*)=1$的那些 $x^*$和其他 $x$在相位图上的差异,最总轻易地找出解:

• (Phase Inversion):这一步主要是把 $x^*$的概率幅翻转,变成负数,而其他的保持不变.即将 $\sum_{x } \alpha_x|x\rangle$变成 $\sum_{x \neq x^*} \alpha_x|x\rangle -\alpha_{x^*}|x^*\rangle$;
• (Inversion about the Mean):将 $\alpha_x$变成 $2\mu- \alpha_x$;

不断的重复这个步骤, $x^*$的概率幅会越来越大,最后测量的时候就会很容易找到 $x^*$.

---

总结

量子计算的基础是量子的叠加态和纠缠现象,而背后这种性质蕴含的是指数级别的算力潜力.在短短的一学期的课时里只能对量子计算的整个脉络有大概的了解,因此撰写一篇能涵盖以上主题的读书报告的同时事实上也容易包含一些低级错误.

(当前的疑惑和之后的学习计划):在掌握了一些量子计算的基础知识后,虽然只能算得上是入门,但是还是感觉量子计算确实充满了吸引力,以后我会持续深入学习其中的某个主题,尤其我对如何实现Grover算法仍然存在一些疑惑(因此在本文中我也没有写如何编程实践Grover算法),其中有些细节问题还需继续深入调研.之后的计划是针对量子电路方面的知识和量子物理里的一些基本概念深入学习,并且会坚持尽可能编程实践.