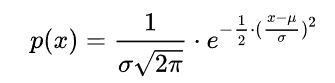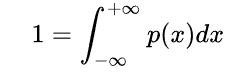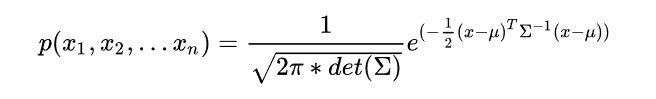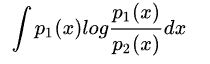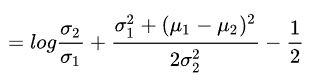深度学习/机器学习入门基础数学知识整理（八）：中心极限定理，一元和多元高斯分布

中心极限定理

设随机变量X1，X2，…Xn，独立同分布，并且具有有限的数学期望和方差： $E(X_i)=\mu$， $D(X_i)=\sigma^2$，则对任意实数x，分布函数

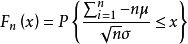
满足

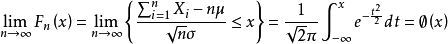
该定理说明，当n很大时，随机变量

近似地服从标准正态分布N(0，1)。因此，当n很大时，

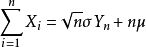
近似地服从正态分布 $N(nμ，nσ2)$．该定理是中心极限定理最简单又最常用的一种形式，在实际工作中，只要n足够大，便可以把独立同分布的随机变量之和当作正态变量。这种方法在数理统计中用得很普遍，当处理大样本时，它是重要工具。

中心极限定理的简单应用

参考资料[1]

高斯分布

高斯分布Gaussian distribution，也叫正太分布Normal distribution，是一个在数学、物理及工程等领域都非常重要的概率分布，在统计学的许多方面有着重大的影响力。

一元高斯分布

若随机变量符合一元高斯分布 $X\sim N(\mu,\sigma^2)$，则有如下的概率密度函数

满足

而如果我们对随机变量 $X$进行标准化 $Z = \frac{X-\mu}{\sigma }$, 那么变量 $Z$服从0均值，1方程的一元标准高斯分布。

多元高斯分布

多维高斯分布的公式：

其中 $x=(x_1,x_2,...,x_n)$为一个n维向量， $\mu$是均值向量， $\sum$是协方差矩阵。

多元高斯分布的的线性变换

两个高斯分布的KL散度

参考资料[5]

两个一元（一维）高斯分布的KL散度 $KL(p_1||p_2)$：

两个多维高斯分布的KL散度 $KL(p_1||p_2)$：

这个在VAE算法中会用到，记录一下，如果看VAE的时候可以查阅。

参考资料

[1] 中心极限定理，百度百科
[2] https://zhuanlan.zhihu.com/p/38501770
[3] https://zhuanlan.zhihu.com/p/58987388
[4] https://zhuanlan.zhihu.com/p/90272131
[5] VAE（1）——从KL说起