POJ -3641Pseudoprime numbers【筛素数+快速幂+欧拉函数降幂】

Disciption
Fermat’s theorem states that for any prime number p and for any integer a > 1, a^p = a (mod p). That is, if we raise a to the pth power and divide by p, the remainder is a. Some (but not very many) non-prime values of p, known as base-a pseudoprimes, have this property for some a. (And some, known as Carmichael Numbers, are base-a pseudoprimes for all a.)

Given 2 < p ≤ 1000000000 and 1 < a < p, determine whether or not p is a base-a pseudoprime.

Input
Input contains several test cases followed by a line containing “0 0”. Each test case consists of a line containing p and a.

Output
For each test case, output “yes” if p is a base-a pseudoprime; otherwise output “no”.

Sample Input

3 2
10 3
341 2
341 3
1105 2
1105 3
0 0

Sample Output

no
no
yes
no
yes
yes

题意
给定一个公式：a^p = a (mod p)，其中2 < p ≤ 1000000000。
求解在p不是素数的情况下是否满足这个式子。

思路ru
手下要判断p是不是素数，因为p很大所以不能直接用筛法，直接暴力到sqrt(n)判断我没试过,怕超时。
我是先筛法求素数到1e5，再暴力判断1e5内的素数是否存在p的因子，去过不存在p的因子，则直接输出no
如果存在则继续判断，因为p过大，所以直接快速幂肯定会爆。这时候需要采用欧拉函数降幂，公式如下：

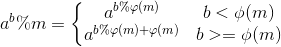
参考这一道题

AC代码

#include<iostream>
#include<cstdio>
using namespace std;
typedef long long ll;
const int N = 100000 + 5;
bool prime[N];//prime[i]表示i是不是质数
int p[N], tot;//p[N]用来存质数

void init()
{
    for(int i = 2; i < N; i ++)
        prime[i] = true;//初始化为质数
    for(int i = 2; i < N; i++)
    {
        if(prime[i])
            p[tot ++] = i;//把质数存起来
        for(int j = 0; j < tot && i * p[j] < N; j++)
        {
            prime[i * p[j]] = false;
            if(i % p[j] == 0)
                break;//保证每个合数被它最小的质因数筛去
        }
    }
}


///直接求解一个数n的欧拉函数
ll euler(ll n)  //返回euler(n)
{
    ll res=n,a=n;
    for(ll i=2; i*i<=a; i++)
    {
        if(a%i==0)
        {
            res=res/i*(i-1);//先进行除法是为了防止中间数据的溢出
            while(a%i==0)
                a/=i;
        }
    }
    if(a>1)
        res=res/a*(a-1);
    return res;
}

ll qmi(ll m, ll k, ll p)
{
    ll res = 1 % p, t = m;
    while (k)
    {
        if (k&1)
            res = res * t % p;
        t = t * t % p;
        k >>= 1;
    }
    return res;
}

ll pp,a;
int f;

int main()
{
    init();
    while(~scanf("%lld %lld",&pp,&a))
    {
        if(pp==0&&a==0)
            return 0;
        f=0;
        for(int i=0; i<tot; i++)
            if(pp%p[i]==0&&pp!=p[i])
            {
                f=1;
                break;
            }
        if(f==0)
        {
            printf("no\n");
            continue;
        }
        ll res=euler(pp);
        ll tmp=qmi(a,pp%res+res,pp);
        if(tmp==a)
            printf("yes\n");
        else
            printf("no\n");
    }
    return 0;
}