对抗机器学习——FGSM经典论文 EXPLAINING AND HARNESSING ADVERSARIAL EXAMPLES

EXPLAINING AND HARNESSING ADVERSARIAL EXAMPLES

论文URL

http://users.wpi.edu/~kmus/ECE579M_files/ReadingMaterials/LinearPerturbation-Goodfelow-1412.6572.pdf

论文核心思想：

对抗样本的存在不是因为深度学习模型的非线性，恰巧相反是因为深度模型的线性。高纬空间的线性行为足以生成对抗样本。基于这种思想作者提出Fast gradient Sign的寻找对抗样本的方法，这种方法也同时可以嵌入到目标损失中作为一种正则化方法去提高模型的鲁棒性。但是这种正则化与dropout啥的正则化有本质的区别。

Szegedy et al. (2014b)的研究结果表明，目标的机器学习分类器尽管能够在测试集上获得优异的性能，但是它们并没有学习到隐藏在问题背后的本质。这些算法只是学习到了训练集上一些流于表面的特征，对于不在训练集数据分布的样本它们的性能是特别差的。

目前神经网络具有非线性的建模能力，但是为了能够让模型收敛，我们又不得不把模型朝线性的方向去设计。对抗样本的出现，更加实锤了神经网络的近似线性性。模型简单带来易受攻击的风险，未来需要设计更加厉害的优化器来让神经网络即可以拥有名副其实的非线性能力，也可以被很的训练。。。。

对抗样本的线性解释

在许多现实问题，输入特征都有精度的限制。例如，对于RGB的三个通道的色彩取值来说，各个通道的取值范围在0-255。这个结果其实是离散化后的结果，即对于实际的色彩强度φ，它可能是个的实数，为了便于计算机表示，于是对φ进行离散化，把它的取值范围离散化256份，对每一份之间的微小变化都被忽略不计。

对于一个原始样本x,它的对抗样本为 $\hat x=x+\delta$ ,其中 $δ$是一个微小的扰动向量，而且要求 $||δ||_∞<ε$，也就是说 $δ$ 的每个分量的绝对值都要小于ε 。在图像领域，如果这个ε 刚好是RGB的精度，那么机器学习模型理应给x和 $\hat x$ 标注相同的结果。
考虑x ̃和一个线性模型的权重向量ω之间的激活值：
$ω^T\hat x=ω^T(x+δ)=ω^Tx+ω^Tδ$
可以看到在加上 $δ$ 这个扰动向量后，线性模型的激活值增加了 $ω^T δ$。现在我们寻找合适的 $δ$ 把这个增量最大化。即：

$max⁡ \space ω^T δ$
$s.t. \space ||δ||_∞<ε$

我们把这个式子写的好看一些：
$max⁡ ∑_{i=1}^{n}{ω_i δ_i}$
$s.t. \space δ_i<ε,i=1..n$

显然要使目标函数取的最大，保证每一项 $ω_i δ_i$最大就可以了。 $ω_i δ_i$最大是 $||ω_i ε||$，于是取令 $δ_i=ε×sign(ω_i)$ 即可取到最大值。

如果w是n维的，每一维的平均大小为m,那么添加扰动后线性模型的激活值平均增加εmn,当维度很高的时候，尽管输入样本x的每一维的变化是很小，但是经过w的维数放大后，我们可以观察到激活值可以增加的很大很大。

这个解释可以说明，为什么简单的线性模型，当维度很高的时候，也会存在对抗样本。

非线性模型的线性扰动

作者假设，目前的神经网络虽然号称是非线性模型，但是它们的表现其实是特别线性的，以致于这些模型连线性扰动都对抗不了。LSTM，Relu，maxout为了训练模型的简单化，都把想方设法把它们按线性的方式设计。

作者假设对于一个神经网络来说，目标函数J和输入x之间其实是存在着近似的线性关系的（这种线性关系可能只是个近似，不是严格数学定义上的线性），即存在w,使得 $J(θ,x,y)≈w^T x$ 。然后根据上面的线性模型的理论，我们给输入x加上一个扰动δ，使得 $w^T δ$ 最大，显然 $δ=ε× sign(w)$。而w可以通过 $∇_x J(θ,x,y)$来求。

于是通过这个方法，我们可以得到一个对抗样本： $x=x+ε×sign(∇_x J(θ,x,y))$。这个对抗样本的效果是什么呢？ 它的效果是使目标函数 $J(θ,x,y)$ 增加最大! 而神经网络中本意是为了最小化这个 $J(θ,x,y)$，现在添加一个扰动后目标函数值就不是最小咯！

那如果是有目标攻击呢,此时对抗样本就应该是 $x=x-ε×sign(∇_xJ(θ,x,T))$，需要体会这里为啥是减：对于有目标攻击，对抗样本的目的是让损失函数在标签T上的函数值越小越好，这样模型才会把T当成样本的label，于是就应该减少在标签T上面的激活值。
作者发现，这种方式很好使。

如上图所示，输入图片是熊喵，然后加了sign后，就得出其它错误的识别结果，而且更搞笑的是错误标签的置信度居然99.3%!!! 个人认为，对抗样本 $x+ε×sign(∇_x J(θ,x,y))$ 会把原来在panda那个标签上的损失变的很大，自然而然的panda的logit或softmax的值会变的很小，从而把原来属于panda的logit都分配出去了？？？但是 还是无法解释为啥置信度会这么高。。。
实验复现并没有出现 对抗样本的错误标签置信度特别高的现象。 因此，作者的这个结果可能只是个巧合。

对抗训练

作者提出往神经网络添加一个 $J(θ,x+εsign(∇_xJ(θ,x,y) ))$ 正则化项的思想，这种思想的含义是说：

对抗样本 $x+ J(θ,x+εsign(∇_xJ(θ,x,y) ))$会使得目标函数在标签y上的损失变得特别大，为了防止这种攻击干脆就在训练阶段把它加入到目标函数中使得就算攻击者搞这么一个攻击样本过来，它能导致的 $J(θ,x+εsign(∇_xJ(θ,x,y) ))$ 也是被最小化过的，它的破坏作用是有限的。

另外一种理解是在训练阶段加入 $J(θ,x+εsign(∇_xJ(θ,x,y) ))$，同时最小化包含这个项的J，其实是在训练阶段强行自己构造了一个新样本： $x+εsign(∇_xJ(θ,x,y) )$ ，并把这个样本的label设置为y。这样当测试阶段，遇到 $x+εsign(∇_xJ(θ,x,y) )$这种对抗样本时就不会瞎猜了。

为啥对抗样本具有迁移性呢？

对抗样本具有很奇特的迁移性：

• 从一个模型训练得到的对抗样本，经常会使其它模型也分类错误，这种模型具有不同的结构，训练集也可能不相交（注意，只是不相交，但是训练集都得满足同一样本分布；可以理解为，把一个大的训练集划分10份，每份训练一个模型）。

  作者认为这个是因为对抗样本是很常见的，它有点类似于实数域里面的有理数的分布，很常见，但是也是在特定的位置常见。
  
  
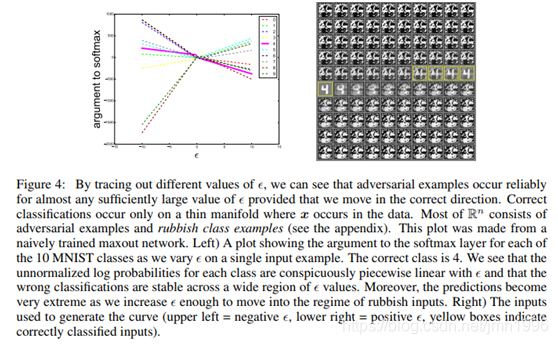
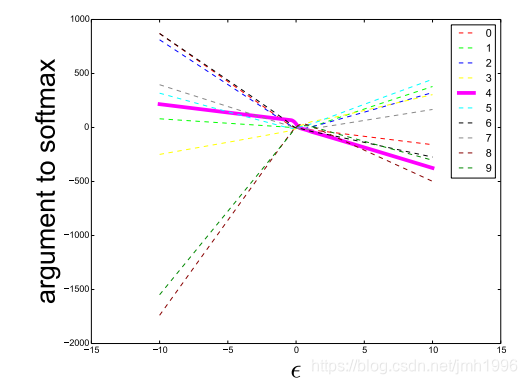
  这个图显示当ε 从小到大取的时候，各个标签的logit的增长。首先，logit的增长与ε 分段线性的，这个更加实锤了神经网络的近似线性性。其次，ε 大于0的时候，正确标签4的logit是负增长的。Ε小于0的时候，正确标签的logit是正增长。

• 同一对抗样本，不同模型甚至给接近的错误label !
  作者认为这个因为目前的机器学习模型，在同一个分布的不同训练集训练得到的模型行为其实是相似的，它们的近似线性权重是同向甚至是相似的！

  为了验证这一点 ，作者在maxout网络找到一些对抗样本。然后拿这些对抗样本去攻击浅层的softmax网络和浅层的RBF网络。对于这些对抗样本，RBF只给出了16%的和maxout相同的错误标签，而softmax网络中54%的错误标签是与maxout相同的。