********Catalan数*********
Catalan数(卡塔兰数)取自组合数学中一个常在各种计数问题出现的数列。卡塔兰数的一般项公式为:
令其为h(n)的话,满足h(n)=h(0)*h(n-1)+h(1)*h(n-2)+......+h(n-1)h(0) (n>=2).若从中取出的数叫做第n个Catalan数,前几个Catalan数是:
1,1,2,5,14,42,132,429,1430,4862,16796,58786,208012,742900,2674440,9694845,.........这么一看没有什么特别的,但是Catalan数却是许多计数问题的最终形式
卡塔兰数的变形:
Catalan数的程序求解:
long Catalan(int n){
if(n<=1) return 1;
long *h=new long[n+1]();
h[0]=h[1]=1;
for(int i=2;i<=n;i++){
h[i]=0;
for(int j=0;j<i;j++) h[i]+=(h[j]*h[i-1-j]); //根据公式h(i)=h(0)*h(i-1)+h(1)*h(i-2)+......+h(i-1)h(0);
}
long result=h[n]; delete []h;
return result;
}
********Catalan数常见的应用********
1->括号的匹配问题(n对括号有多少种匹配方式?)
解题:n对括号相当于2n个符号,n个左括号、n个右括号,可以设问题的解为f(2n).第0个符号肯定为左括号,与之匹配的右括号必须为2*i+1.因为如果是第2*i个字符,那么第0个字符与第2i个括号之间包含了奇数个括号,无法构成匹配。
通过分析,f(2n)可以转化为如下的递推式f(2n)=f(0)*f(2n-2)+f(2)*f(2n-4)+.....+f(2n-4)*f(2)+f(2n-2)*f(2).该递推式的解释如下:f(0)*f(2n-2)表示第0个字符与第1个匹配。同时剩下的字符分成两部分,一部分为0个字符,另一部分分为2n-2个字符,然后分别对这两部分进行求解。f(2)*f(2n-4)表示第0个字符与第3个字符匹配,剩下部分分成两个一个包含2个括号,一个包含2n-4个括号,依次类推。
假设f(0)=1,计算下面项f(2)=1,f(4)=2,f(6)=5.刚好f(2n)=h(n)
2->进栈出栈问题(一个无穷大的栈,进栈序列为1,2,3,......,n,有多少个不同的出栈序列)
解题:这个与加括号的很相似,进栈操作相当于是左括号,而出栈操作相当于右括号,n个数的进栈次序和出栈次序构成了一个含有2n个数字的序列。第0个数肯定是进栈的数,第2i+1是出栈的数。同上面一题类似可以用Catalan数方法解决
3->二叉树的种类问题(n个结点构成的二叉树,共有多少种情形?)
可以按照如下的方式考虑:根结点肯定会占用一个结点,那么剩余的n-1个结点可以有如下的分配方式,T(0,n-1),T(1,n-2),T(2,n-3).....T(n-1,0),其中T(i,j)表示根的左子树含有结点i,右子树含有结点j
上述问题用递归式表达:f(n)=f(0)*f(n-1)+f(1)*f(n-2)+......+f(n-1)f(0) 刚好和Catalan数的递推公司相同。
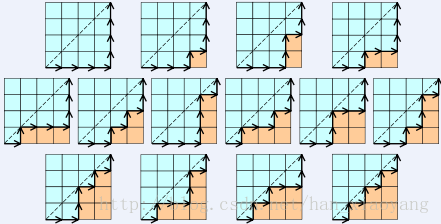
4->网格路径问题
对于一个n*n的正方形网格,每次我们能向右或者向上移动一个格,那么从副对角的左下方到右上方的路径(均在副对角线的下方)总数为多少?
对于这样的题目,我们将一条水平线标记为进栈操作,垂直线标记为出栈操作。要保证前进的k步总水平的格子数多于垂直的格子数。转为理解为出栈的时候必须有元素,很明显又是一个Catalan数问题。
5->凸多边形分割问题(求一个凸多边形区域划分成三角形区域的方法数?)
解题:以凸多边形的一边为基,设这条边的2个顶点A和B,从剩余顶点中选一个,可以将凸多边形分成三个部分,中间一个是三角形,左右两边分别为凸多边形,然后再分别求解这两个凸多边形。
设问题的解f(n),其中n表示顶点的个数,那么f(n)=f(2)*f(n-1)+f(3)*f(n-2)+....+f(n-2)*f(3)+f(n-1)*f(2).其中f(2)*f(n-1)表示相邻三个顶点构成一个三角形,那么另外两个部分的顶点数分别为2和n-1个
设f(2)=1,那么f(3)=1,f(4)=2,f(5)=5,依次类推f(n)=h(n-2)
6->集合划分问题(对于集合1,2,3,....,2n的不交叉的划分数目?)
不交叉的划分定义为:对于集合{a,b}和{c,d},假设它们组成的区间[a,b]和[c,d]我们假设两个区间不重合,那么以下4种为不交叉的情况:a<c<d<b a<b<c<d c<a<b<d c<d<a<b
对于集合{1,2,3,.....2n}将里面的元素两两分为一个子集,共n个,若任意两个子集都是不交叉的,那么我们称此时的划分为一个不交叉划分。我们可以将每个子集中的较小数用左括号代替,较大数用右括号代替,此时就转换位括号匹配问题,用Catalan求解。
7->矩阵连乘问题
矩阵连乘的括号化方案为f(n),那么问题的解为 f(n)=f(1)*f(n-1)+f(2)*f(n-2)+......+f(n-1)*f(1),转化为catalan数为h(1)
8->连线不相交问题(在园上有2n个点,将这些点成对连接起来使得所得的n条线段不想交的方法数?)
我们做这样的考虑,以其中一个点为基点,编号为0,然后按照顺时针方向将其他点依次编号。那么与0号相连的必定为奇数。否则,这两个编号间含有奇数个点。必定会使得有个点被孤立。若两个点相连之后就被划分为两个部分,一个部分含i个点,另一个部分含j个点。有递推式:f(n)=f(0)*f(n-2)+f(2)*f(n-4)+.....+f(n-4)*f(2)+f(n-2)*f(0).点的个数为2n转化为求h(n)
9->高矮排队问题(2n个高矮不同的人,排成两排,每排必须是从矮到高排列,而且第2排比对应第一排的人高,问有多少种排列方式)
先将2n个人从低到高排列,然后用0表示对应的人在第一排,用1表示对应的人在第2排。那么总共有n个0和n个1。那么对应着一种方案:比如0000.....11111对应着第一排为1到n,第2排位n+1到2n 问题就转化为满足这样的01序列的个数。
观察1的出现,我们考虑它能不能放在第2排,那么在这个1之前出现的那些0和1对应的人,要么在1的左边要么在1的前面。就是要求之前0的个数要大于1.我们可以把0看成入栈1看成出栈,这样问题就转为2n个元素的合法出入栈的顺序。Catalan数问题
10->格子填数问题(在一个2*n的格子中填入1到2n这些数值,使得每个格子内的数值都比右边和上边的大)
和第9题问题类似
11->门票找钱问题(2n个人排成一个行进入剧场,入场费5元,其中只有n个人有一张5元的钞票,n个人只有10员的钞票,问排队的方案)
解题方法:将5元的看成进栈,10员的看成出栈,问题转化为n个元素出栈种类的问题