数值运算的要求
1.保证数值稳定型,即在迭代递推的过程中,误差应该逐渐减小,而不是逐渐放大
2.避免相近的两数相减,通过变换消除减法项
3.防止大数“吃掉”小数,注意保护重要物理参数(解方程时和计算绝对值相差较大的加法时)
4.防止溢出
5.简化计算步骤,减少运算次数,避免误差累积
三个简单的算法
(一)正向与反向计算
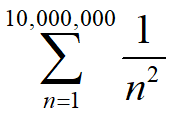
反向计算比正向计算更加精确,因为正向计算会导致大数“吃掉”小数。
上代码:
#include<iostream>
#include<stdio.h>
#include "math.h"
using namespace std;
void main()
{
int i,n;
float temp,sum1,sum2;
n=10000000;
sum1=0.0;
sum2=0.0;
for (i=1;i<=n;i++)
{
temp=1.0/(float)i;
sum1=sum1+temp*temp;
}
printf("the sum1 is %16.12f\n",sum1);
for (i=n;i>=1;i--)
{
temp=1.0/(float)i;
sum2+=temp*temp;
}
printf("the sum2 is %16.12f\n",sum2);
system("pause");
}
(二)秦久韶算法计算多项式
对于一个多项式:
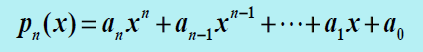
法1:从右往左计算,设置一个中间变量保存x的高次,避免每次都要重新计算高次幂。
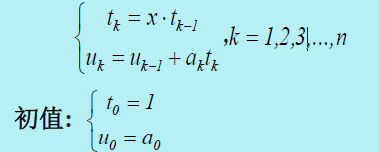
法2:秦久韶算法,对多项式提取公因式
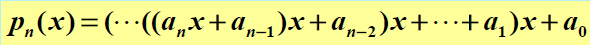
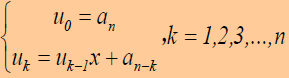
代码:
#include<iostream>
#include<stdio.h>
#include "math.h"
using namespace std;
int function_qin1(int x)
{
int a[6]={1,-1,4,0,-3,1};
int i;
int temp,sum;
sum=a[0];
temp=1;
for(i=1;i<6;i++)
{
temp*=x;
sum+=temp*a[i];
}
return sum;
}
int function_qin2(int x)
{
int i;
int n=6;
int a[6]={1,-1,4,0,-3,1};
int sum;
sum=a[5];
for(i=4;i>=0;i--)
{
sum=sum*x+a[i];
}
return sum;
}
void main()
{
cout<<"the result is"<<function_qin1(3)<<endl;
cout<<"the result is"<<function_qin2(3)<<endl;
system("pause");
}
(三)一元二次方程求根
1.利用求根公式求解绝对值大的根
2.利用韦达定理求解绝对值较小的根

代码(跟流程图存在一些差异):
#include <iostream>
#include "math.h"
#include <stdio.h>
using namespace std;
void Solve_equation(double b,double c,double *ptr)
{
float d;
d=(b*b-4*c);
//判断d的正负
if(d<0)
{
cout<<"error"<<endl;
return;
}
else
{
d=sqrt(d);
//判断b的正负,然后找到绝对值大的解
if(b>0)
{
//绝对值大的解
(*ptr)=(-b-d)/2;
//利用韦达定理求解另一根
(*(ptr+1))=c/(*ptr);
}
else
{
//绝对值大的解
(*ptr)=(-b+d)/2;
//利用韦达定理求解另一根
(*(ptr+1))=c/(*ptr);
}
}
cout<<"the x1 is"<<(*ptr)<<"the x2 is"<<(*(ptr+1))<<endl;
}
void main()
{
double x[2];
double b=-(1+10e9),c=10e9;
Solve_equation(b,c,x);
system("pause");
}
(四)方程求根的二分法
前提:单调函数,且区间内存在根
算法描述:
1.取区间中点为根
2.判断根的函数值与上限的函数值的乘积是否大于0
3.如果大于0则说明实际根位于下限与当前跟之间
4.更新区间
5.迭代,直到误差范围小于要求(误差即为上下限之差/2)
代码:
#include <iostream>
#include <stdio.h>
#include <math.h>
using namespace std;
float Equation_function(float x)
{
return pow(x,3)-x-1;
}
float Dichotomy_solution(float error_range,float down,float upper)
{
float error=(upper-down)/2;
float x;
float y,y0,y1; //用来记录x,upper,down的函数值
int count=0;
while(error>=error_range)
{
//找到当前上下限对应的解以及误差
x=(upper+down)/2;
error=(upper-down)/2;
//计算此时的x,upper,down对应的函数值
y=Equation_function(x);
y0=Equation_function(down);
y1=Equation_function(upper);
if((y*y1)<0)
{
down=x;
}
else if((y*y1)==0)
{
return x;
}
else
{
upper=x;
}
}
return x;
}
void main()
{
float x;
x=Dichotomy_solution(1e-3,1,2);
cout<<"x is "<<x<<endl;
system("pause");
}
