支持向量机的原理简单概括来说,就是在样本空间寻找最佳分类面即超平面,将训练样本分开。对于样本空间,可能存在多个划分超平面将两类训练样本分开,如下图所示的情况:
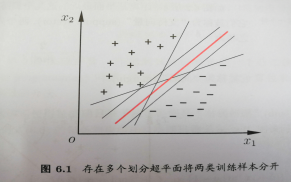
那么从上图来看显然正中间的红色的超平面是我们所要找的超平面,因为受到训练样本数量上的限制以及噪声、误差等因素的干扰,该超平面受到的影响最小,即对分类结果最鲁棒。
在样本空间中,我们通过下述方程来描述超平面:
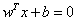
其中w=(w1,w2,……wd)为超平面的法向量,决定了超平面的方向;b为位移项,决定了超平面与原点之间的距离。
根据点到平面的距离公式:
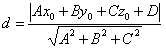
可知,对于样本空间中的任意一点x到超平面的距离可以写为:
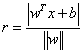
我们假设超平面能将训练样本正确分类,令以下关系成立:


如上图所示,我们定义“支持向量”为能使上述不等关系中等号成立的点,即这些点分别位于平面wTx+b-1=0上和平面wTx+b+1=0上。至于两个平面为什么分别位于超平面wTx+b=0的上侧和下侧,通过matlab程序跑一下便知。
我们分别令三个平面x+y+z=0,x+y+z=1和x+y+z=-1,通过matlab有如下三维平面图象:

除此之外,我们定义在平面wTx+b=1上及其上侧的点的类别标签为“+1”类,在平面wTx+b=-1上及其下侧的点的类别标签为“-1”类。根据两平行平面之间的距离公式,如果存在两个平行平面Ax+By+Cz+D1=0,Ax+By+Cz+D2=0,则这两个平面之间的距离为
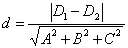
由此我们可以得到平面wTx+b=1和wTx+b=-1之间的距离为
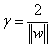
此距离被称为“间隔”(两个异类支持向量到超平面的距离之和)。欲找到具有“最大间隔”的划分超平面,即寻找满足约束条件
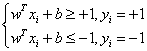
的参数w和b,使得γ最大化。上述问题即可转化成如下数学模型:
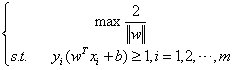
该数学模型的第二个式子是超平面能进行正确划分的约束条件。如果样本数据集能正确划分,不论原来样本数据的标签是+1还是-1,yi(wTxi+b)的值均会是大于等于1的正数。为了最大化间隔,我们通常将上述问题转为其对立面,即要想最大化2/||w||就等价于最小化||w||2。于是上述数学模型可以重写为
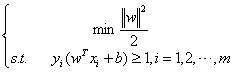
以上就是支持向量机的基本模型。
我们发现上述模型是一个凸二次规划问题,下面引入SMO算法模型。
上述问题我们可以利用拉格朗日函数将其转化为对偶问题。对上述模型中的每条约束条件添加拉格朗日乘子αi≥0,则该问题通过拉格朗日函数可以写成如下形式:
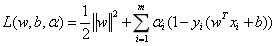
我们将做如下的问题变换:
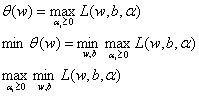
原来问题模型明明是求的最小化,为什么突然变成最大化数学模型了呢?个人的理解就是,如果对于距离超平面最近的点即支持向量都能满足约束条件即能正确分类,那么对于其他样本空间中的点亦能成立。也就是说,我们首先要找到支持向量,然后再将间隔最大化。
我们令拉格朗日函数L对w和b的偏导数为零可得
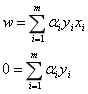
于是以上两个等式代入
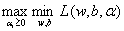
中可写成
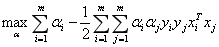
对于
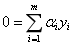
中如果我们每次选择两个变量α,然后固定剩余参数,那么其中一个变量可以由另外一个变量导出。这样我们每次仅优化两个参数,可以做到非常高效。即
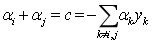
所以
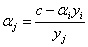
再将
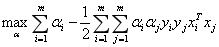
中的αj替换掉就转换成了αi的单变量二次规划问题。
如何确定偏移项b呢?我们发现对于任意支持向量(xs,ys)都有ysf(xs)=1成立(f(x)=wTx+b),即
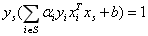
上述式子中,S是所有支持向量的下标集,理论上可以通过上式求解得到b。但是现实中我们通常采用更准确更具鲁棒性的方法求解b,即使用所有支持向量求解的平均值:
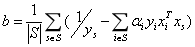
支持向量机基本原理
猜你喜欢
转载自blog.csdn.net/qq_38883271/article/details/103667949
今日推荐
周排行
