关于满二叉树的一个证明

本文简单给出了在满二叉树中 内部节点数目( $C_i$) = 叶子节点数目( $C_l$) - 1 的两种证明方法

二叉树大家都不陌生,但是分类上可能大家就不那么熟稔了,本篇博文中提到的所谓满二叉树,定义上也有些分歧,在此我们采用如下定义:

满二叉树(Full Binary Tree),即只存在 度为 0 的节点(叶子节点) 和 度为 2 的节点(内部节点) 的二叉树
(定义中提到的 “度” 即为二叉树节点的分支数目)

根据这个定义,以下的二叉树都是满二叉树:

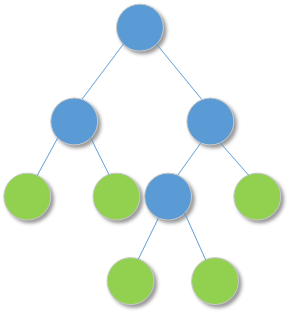
而下面的二叉树则不是满二叉树,因为存在度为 1 的内部节点:

满二叉树中节点数目满足以下等式:(设叶子节点的数目为 $C_l$, 内部节点的数目为 $C_i$)

$C_i = C_l - 1$

证明方法一

上述结论的一般证明方法是这样子的:

• 首先考虑满二叉树的分支数目(设为 $B$)对应的节点数目:

由于除根节点外,所有分支都对应一个节点,所以我们有:

$B = C_i + C_l - 1$

• 再次考虑满二叉树的节点数目对应的分支数目:

由于叶子节点对应 0 个分支(度为 0),内部节点对应 2 个分支(度为 2),所以我们有:

$B = C_i * 2 + C_l * 0$

综合上面两式,我们即可证明结论:

$C_i = C_l - 1$

证明方法二

实际上,我们还可以使用数学归纳法来证明:

考虑基础情况(只有一个根节点(或者说一个叶子节点)):

此时我们有:

$C_l = 1, C_i = 0$

显然满足等式.

接着我们对一般情况进行归纳,由于是满二叉树的关系,所以一般情况一定满足下面的树形结构:

图中的左右子树也都是更小规模的满二叉树.

我们设

• 左子树中的叶子节点数目和内部节点数目分别为 $Cl_l$ 和 $Cl_i$
• 右子树中的叶子节点数目和内部节点数目分别为 $Cr_l$ 和 $Cr_i$

于是我们有:

$\begin{aligned} & Cl_l + Cr_l = C_l & (1)\\ & Cl_i + Cr_i + 1 = C_i & (2)\\ & Cl_i = Cl_l - 1 & (3)\\ & Cr_i = Cr_l - 1 & (4)\\ \end{aligned}$

将 $(3)$ $(4)$ 代入 $(2)$, 我们有:

$\begin{aligned} & Cl_l - 1 + Cr_l - 1 + 1 = C_i \\ & => \\ & Cl_l + Cr_l - 1 = C_i \end{aligned}$

再代入 $(1)$, 我们即可得出结论:

$C_l - 1 = C_i$

参考资料

• 二叉树
• 关于二叉树中度为0与度为2节点数关系证明