粒子在磁镜场中的运动

磁镜场的特征是磁场强度在沿着磁力线的方向有变化。这种空间变化会导致粒子的导向中心平行于磁场方向的运动被反射，因而叫做磁镜场。考虑一个轴对称的磁场，在柱坐标系下， $\rho$为到对称轴的距离， $\phi$为绕对称轴的角度， $z$在对称轴上的位置。如果磁场强度沿着磁力线增加，那么根据Maxwell散度方程 $\bm{\nabla \cdot B}=0$可以知道，沿着对称轴，磁力线必定会聚集。从Maxwell散度方程可以导出聚集速率
$\bm{\nabla \cdot B}=\frac{1}{\rho}\frac{\partial}{\partial\rho}(\rho B_\rho)+\frac{\partial B_z}{\partial z}=0$

将方程对 $\rho$ 积分，并设 $\frac{\partial B_z}{\partial z}$与 $\rho$无关
$\frac{\partial}{\partial \rho}(\rho B_\rho)=-\rho \frac{\partial B_z}{\partial z} \\ \rho B_\rho＝-\frac{1}{2}(\frac{\partial B_z}{\partial z} )\rho^2 \\ B_\rho＝-\frac{1}{2}(\frac{\partial B_z}{\partial z} )\rho$

或者
$B_x＝-\frac{1}{2}(\frac{\partial B_z}{\partial z} )x \\ B_y＝-\frac{1}{2}(\frac{\partial B_z}{\partial z} )y$

若 $\frac{\partial B_z}{\partial z}$为正值，则沿着 $+z$方向，磁力线聚集，磁场强度增加。这个方程只有在对称轴附近在成立，因为积分时假设了 $\frac{\partial B_z}{\partial z}$与 $\rho$无关。

1、平行运动

平行方向的运动方程为
$F_z=\frac{dv_z}{dt}=q(v_xB_y-v_yB_x)$

将上述的 $B_x$与 $B_y$代入，得
$F_z=-\frac{q}{2} (\frac{\partial B_z}{\partial z}) (v_xy-v_yx)$

若磁场变化足够缓慢，则横向运动可以看成是圆周运动，有
$x=\rho_c\sin(\omega_ct) \\ y=\frac{q}{|q|} \rho_c\cos(\omega_ct) \\$

对 $t$求导，得到速度
$v_x=\omega_c\rho_c\cos(\omega_ct) \\ v_y=-\frac{q}{|q|} \omega_c \rho_c\sin(\omega_ct) \\$

从而 $z$方向的受力为
$F_z=- \frac{\partial B_z}{\partial z} (\frac{|q|}{2}\omega_c\rho_c^2)$

将括号中的项 $\frac{|q|}{2}\omega_c\rho_c^2$为磁矩
$\mu=\frac{w_\bot}{B}＝\frac{\frac{1}{2}mv_\bot^2}{B}$

所以
$F_z=-\mu \frac{\partial B_z}{\partial z}$

将上述方程写成矢量形式，磁矩的方向与磁场反向（磁矩方向与粒子回旋运动方向成右手螺旋关系），可以得到平行于磁场方向的受力为
$\bm{F}=(\bm{\mu \cdot \nabla})\bm{B}$

因此，粒子在非均匀磁场中运动时，平行磁场方向的受力可以看成是磁场与粒子回旋运动产生的磁矩之间的相互作用，其作用效果是使粒子从强磁场区域反射回去。这个力本质上是Lorentz力在对称轴上的分量

2、垂直运动

上面考虑了平行运动，在垂直方向上Lorentz力也有分量
$F_\phi=qv_zB_\rho$

这个力产生了一个力矩，引起粒子垂直方向动能的变化。其变化率
$\frac{dw_\bot}{dt}=v_\phi F_\phi=qv_\phi v_z B_\rho$

将开始时的 $B_\rho$代入，并且 $v_\phi = －(q/|q|)v_\bot$ （极坐标系下沿逆时针方向旋转为正），上述方程化为
$\frac{dw_\bot}{dt} = \frac{1}{2}|q|v_\bot v_z (\frac{\partial B_z}{\partial z} ) \rho$

虽然粒子的垂直方向与平行方向的动能都会变化，但是粒子的总动能是不变的（Lorentz力与粒子速度方向垂直）。将上面的 $\rho$用粒子的回旋半径 $\rho=mv_\bot/|q|B$替换，得到
$\frac{dw_\bot}{dt} = \frac{w_\bot v_z}{B} (\frac{\partial B_z}{\partial z})$

考虑磁矩的变化
$\frac{d\mu}{dt} = \frac{d}{dt}(\frac{w_\bot}{B}) = \frac{1}{B}\frac{dw_\bot}{dt} - \frac{w_\bot}{B^2} \frac{dB}{dt}$

这里磁场不随时间变化，仅沿 $z$方向有变化，且磁场主要沿 $z$方向，将磁场的全微分拆开
$\frac{dB}{dt} = \frac{\partial B}{\partial t} + v_z \frac{\partial B}{\partial t} = v_z \frac{\partial B_z}{\partial t}$

得到
$\frac{d\mu}{dt} = \frac{1}{B}\frac{dw_\bot}{dt} - \frac{w_\bot v_z}{B^2}(\frac{\partial B_z}{\partial t})$

替换垂直动能变化率，可得
$\frac{d\mu}{dt}= \frac{w_\bot v_z}{B^2}(\frac{\partial B_z}{\partial t}) - \frac{w_\bot v_z}{B^2}(\frac{\partial B_z}{\partial t}) = 0$

即磁矩不随时间，磁矩守恒（第一绝热不变量）。

3、反转点

考虑粒子平行方向的运动方程
$m \frac{dv_\parallel}{dt} = -\mu \frac{\partial B}{\partial z}$

将 $v_\parallel$对时间的导数变换为对位置的导数
$\frac{dv_\parallel}{dt} = \frac{dv_\parallel}{dz} \frac{dz}{dt} = v_\parallel \frac{dv_\parallel}{dz}$

方程化为
$\frac{d}{dz} ( \frac{1}{2}mv_\parallel^2 + \mu B ) = 0$

这意味着
$\frac{1}{2}mv_\parallel^2 + \mu B(z) = \mu B_m$

其中 $\mu$ 和 $B_m$ 是常量。该方程可以看成是在一维势井中运动的粒子的平行动能转化方程。在 $z_1$、 $z_2$处，粒子的平行动能为零。
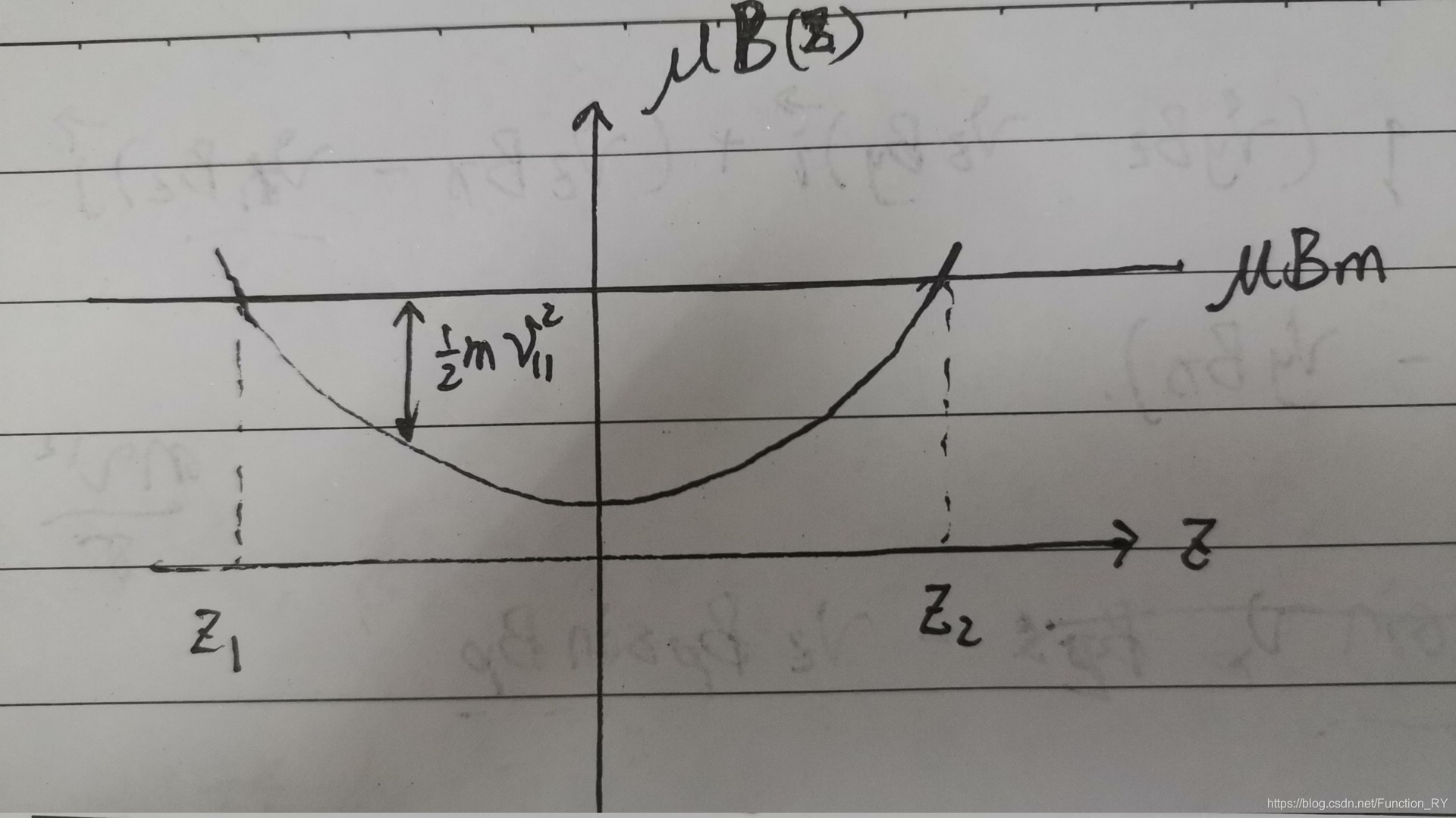此时 $B(z_1)=B(z_2)=B_m$， $\mu B_m$为粒子的总动能
$w = \mu B_m$
从该方程可以解出粒子的平行速度
$v_\parallel = \pm \sqrt{\frac{2\mu}{m}(B_m - B)}$

设粒子速度与磁场的夹角为 $\alpha$（投掷角），则
$v_\bot = v \sin \alpha \\$

从而得到磁矩
$\mu = \frac{w_\bot}{B} = \frac{w \sin ^2 \alpha}{B}$

由于
$w=\mu B_m \\ w_\bot = \mu B$

可以得到
$\sin ^2 \alpha =\frac{B}{B_m}$

对于给定磁矩和给定能量的粒子，可以通过这个方程来计算沿着磁力线上任意一点的投掷角。

对于一个典型的磁镜（中间磁场弱，两端磁场强），设最强的磁场为 $B_{max}$， 最弱的磁场为 $B_{min}$，要使粒子发生反射的最小投掷角为 $\alpha_0$，则有
$\sin^2 \alpha_0 = \frac{B_{min}}{B_{max}}$

若粒子的投掷角小于 $\alpha_0$，则磁镜无法束缚住该粒子。将绕着磁力线立体角成 $\alpha_0$的锥体称为损失锥，投掷角在损失锥内的粒子将逃逸出磁镜。