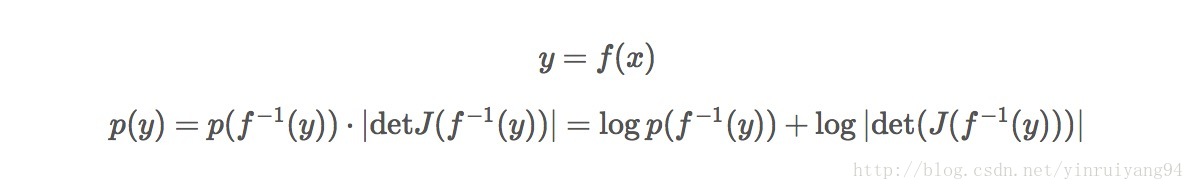如果你是一个机器学习的实践者致力于生成模型、贝叶斯深度学习,或深度强化学习,normalizing flows是一个你算法工具包中方便的技术。normalizing flows变换简单的密度(如高斯函数)成为丰富复杂的分布,可用于生成模型,RL和变分推断。
这个Tutorial由两部分组成:
1. 分布和决定因素:在这篇文章中,我解释了如何使用可逆转换的密度来实现更复杂的密度,以及这些转换可以链接在一起,形成一个“normalizing flows”。
2. modern normalizing flows
本文是为对线性代数、概率、神经网络和tensorflow有初步了解的观众写的。深度学习的最新进展,生成模型将有助于理解潜在的动机和背景这些技术,但它们并不是必要的。
背景
统计机器学习试图学习数据的结构来拟合一个分布p(x;θ)。对于一个数据集,如果我们可以用一个分布表示它,我们就可以:
1.通过在学习来的分布中采样来生成新的数据;不需要对数据执行真正的生成过程。这对于那种生成代价大的数据是一个有用的方式,举例说,一个真实世界的需要运行很久的实验。采样也可以用来构造空间中高维积分的评估者。
2.在测试时评估观察到的数据的似然。
3.发现变量之间的条件关系。例如,学习分布p(x2 | x1)允许我们构建对抗分类或回归模型
4.评分我们的算法通过使用复杂的措施例如熵,互信息,某一刻的分布。
我们已经很擅长抽样(1),最近的研究证明了这一点上生成模型图像和音频。这些类型的生成模型已经被部署在实际商业应用和谷歌产品。然而,目前研究团体指导更少的注意力转向无条件&条件似然估计(2、3)和模型评分(4)。例如,我们不知道如何计算的支持GAN解码器(多少输出的空间分配非零概率的模型),我们不知道如何计算图像的密度对平局分配甚至VAE,我们不知道如何分析计算各种指标(KL,挖土机距离)任意分布,即使我们知道他们分析密度。
生成类似的采样是不够的,我们也要回答这个数据到底有多像。具有灵活的条件密度,以及能够选择丰富的先验后后验的变分推理。
正态分布。我们可以很容易地从中得出样本,我们知道它分析密度和KL散度到其他正态分布,中心极限定理给了我们信心,我们可以把它应用到几乎任何类型的数据,正态分布的易用性使其对于许多生成建模和强化学习算法成为一个非常流行的选择。
不幸的是,正态分布并没有削减我们关心的许多现实世界的问题。 在强化学习中 - 特别是连续控制任务,例如机器人 - 策略通常被建模为 multivariate Gaussians with diagonal covariance matrices。
很多的例子说明了正态分布可能过于简单。高斯函数有大部分密度集中在高维度和边缘不健壮的罕见事件。我们可以找到一个更好的分布具有以下属性的吗?
1.足够复杂来建模各种数据分布 例如图像或者RL的环境。
2.同时保留正态分布的简单舒适性
答案是有的,其中之一就是normalizing flows
变量的变化,量的变化
让我们通过检查一维随机变量的线性变换建立一些直觉。设X是分布均匀(0,1)。 Y=f(X)=2X+1。Y是X简单的线性变换。意味着一个X中的采样x,可以轻松的转化成一个Y中的采样,通过上边的公式。如图:
绿色正方形代表p(x)和p(y)上R上的阴影概率质量 - 高度表示该值处的密度函数。
可以看出,因为任何分布的概率质量都必须为1,所以将域乘以2的行为意味着我们必须将概率密度除以2,以使绿色正方形和蓝色矩形的总面积相同。
然后如图搞一些事情:
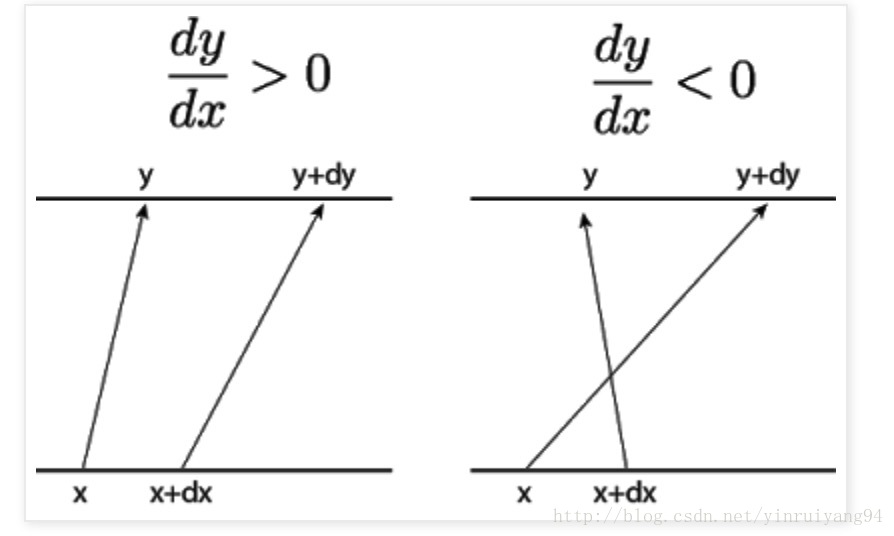
取一个特定的x 和一个x旁边的极小量x+dx ,对应的y就是(y,y+dy) 。
在左边,我们有一个局部递增函数(dy / dx> 0),右边是一个局部递减函数(dy / dx <0)。 为了保持总概率,间隔dx的p(x)的变化必须等于间隔dy的p(y)的变化:
p(x)dx=p(y)dy
接下来,
我们只关心y的变化量而不是它的方向(如果f(x)在x上递增或递减并不重要,我们假设y的变化量是相同的)。
因此,p(y)= p(x)| dx / dy |。
这相当于
logp(y)= logp(x)+ log | dx / dy |。
接下来我们考虑多个变量的情况,以上说的都只有一个x。下边是2个变量。
和单变量一样,还是选定一个特定的x和一个极小量dx,由于是两个变量,他们两个就会组成一个小的边长为dx的正方形。如下图中左边坐标系的绿色部分:
请注意,仅改变矩形块(x1,x2,x3,x4)的转换不会改变区域。 我们只对x的单位面积的变化率感兴趣,所以位移dx可以被认为是一个任意的度量单位。 为了使下面的分析简单,无单位,我们来研究一下原点的单位平方,即4点(0,0),(1,0),(0,1),(1,1)。如上图中右边坐标系中绿色部分。
乘以矩阵[[a,b]; [c,d]](这和一维中ax + b = y一样,是不过是2维的线性变换)将把这个方格上的点变成平行四边形,如右下图所示。 (0,0)成为(0,0),(1,0)成为(a,b),(0,1)成为(c,d),(1,1)成为(a+ c,b+ d)。如上图右边坐标系蓝色所示。
计算单位面积变化率:
X的域中的单位平方对应于Y域中的变形的平行四边形,所以每单位面积的变化率是平行四边形的面积,即ad-bc。
平行四边形的面积ad-bc不过是线性变换行列式的绝对值!
在3维中,“平行四边形面积的变化”变成“平行六面体体积的变化”,甚至更高的尺寸,这成为“n平行体的体积变化”。 但是这个概念仍然是一样的 - 决定因素只不过是线性变换的体积失真量(和方向),推广到任何维数。
如果变换函数f是非线性的呢? 您可以绘制许多无限小的平行四边形,对应于域中每个点的扭曲的量,而不是跟踪空间中任意点的扭曲得到的单个平行四边形。
在数学上,这种局部线性的体积变化是| det(J(f ^-1(x)))|,其中J(f ^ -1(x))是反函数的雅可比矩阵((f ^-1(x))是反函数)。 来自之前的数量dx / dy的更高维广义化。
根据前文的描述,
p(x)dx=p(y)dy
p(y)= p(x)| dx / dy |
logp(y)= logp(x)+ log | dx / dy |
我们可以得到如下图:
我们只被教导如何计算一个行列式,而不是一个行列式代表什么:一个转换的局部线性化的体积变化率。
使用tensorflow变换分布
tensorflow有一个很优雅的转换分布的API,一个转化后的分布由一个我们要去转化的基础的分布目标和以下三点决定:
前向转化函数y=f(x)
其反函数f ^-1(x)
log|detJ(f−1(y))|
此外,如果bijector.forward是一个可微函数,那么Y = bijector.forward(x)是对应样本x = base_distribution.sample()的可重新参数化分布。 这意味着normalizing flows可以用作VAE变换后验的替代(作为高斯的替代)。
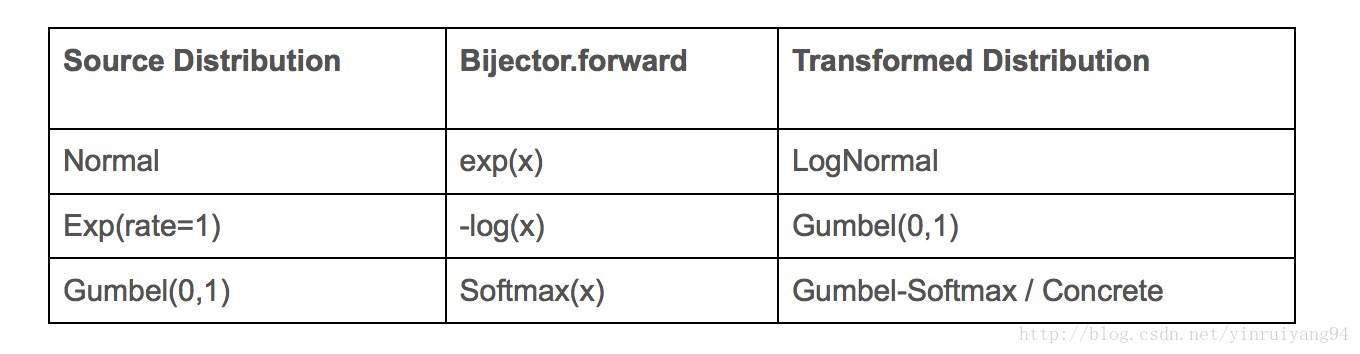
一些常用的TensorFlow分布实际上是使用这些TransformedDistributions实现的。
Normalizing Flows 和学习灵活的映射
为什么就仅仅一层映射就停止了呢?我们可以多几层啊,好几层链式地连在一起,就像神经网络一样。这就称为Normalizing Flows 。此外,如果一个映射有可调的参数对应于bijector.log_prob,这个映射确实可以被学习去转化我们的原始的分布来适应任何的密度。
每一个bijector函数看做一个可学习的“层”,你可以使用一个优化器去学习转化函数的参数来拟合我们的数据的分布。
一种算法是最大似然估计,它修改我们的模型参数,使我们的训练数据点在我们变换的分布下具有最大的对数概率。 我们计算和优化对数概率,而不是数值稳定性原因的概率。